4.2. Алгоритм переноса граничных условий на примере расчёта пластины

Рассмотрим метод на примере двумерной задачи расчёта напряжённо-деформированного состояния жёстко заделанной квадратной пластины. Пластина шириной Ь и толщиной h нагружена давлением q. Поместим её в систему декартовых координат . (рисунок 4.1). Разделим мысленно пластину параллельными линиями на n интервалов по осям X и Y соответственно (штриховые линии на рисунок 4.1). Индекс i соответствует сечениям по оси X, индекс j – сечениям по оси y. Из числа элементов n² выделим один с i-м нижним и j-м левым сечением (рисунок 4.2). Ширина элемента: .

В каждом сечении элемента пластины будет действовать переменная эпюра напряжений. При уменьшении размеров элементов в сечении согласно принципам механики для твердого тела напряжённое состояние можно представить силами, сосредоточенными в центре и моментами. Для таких деформаций пластины с симметричным нагруженном касательными и нормальными силами по осям х и y можно пренебречь [96]. Таким образом в каждом сечении будем учитывать: изгибавший момент М вокруг срединной линии, параллельной плоскости пластины, крутящий момент К и перерезывающую силу , параллельную вертикальной оси Z.

Рисунок 4.1 - Схема расчеления пластины на элементы

Угол поворота от изгибающего момента будем обозначать , угол поворота от крутящего момента - , перемещение в направлении перерезывающей силы –W. На (рисунке 4.2) показано положительное направление этих перемещений. Параметры М, К, , , , w в сечениях, перпендикулярных осям х и у будем снабжать индексами х и у соответственно. Индексы i , j соответствуют номеру сечений по оси x и у.

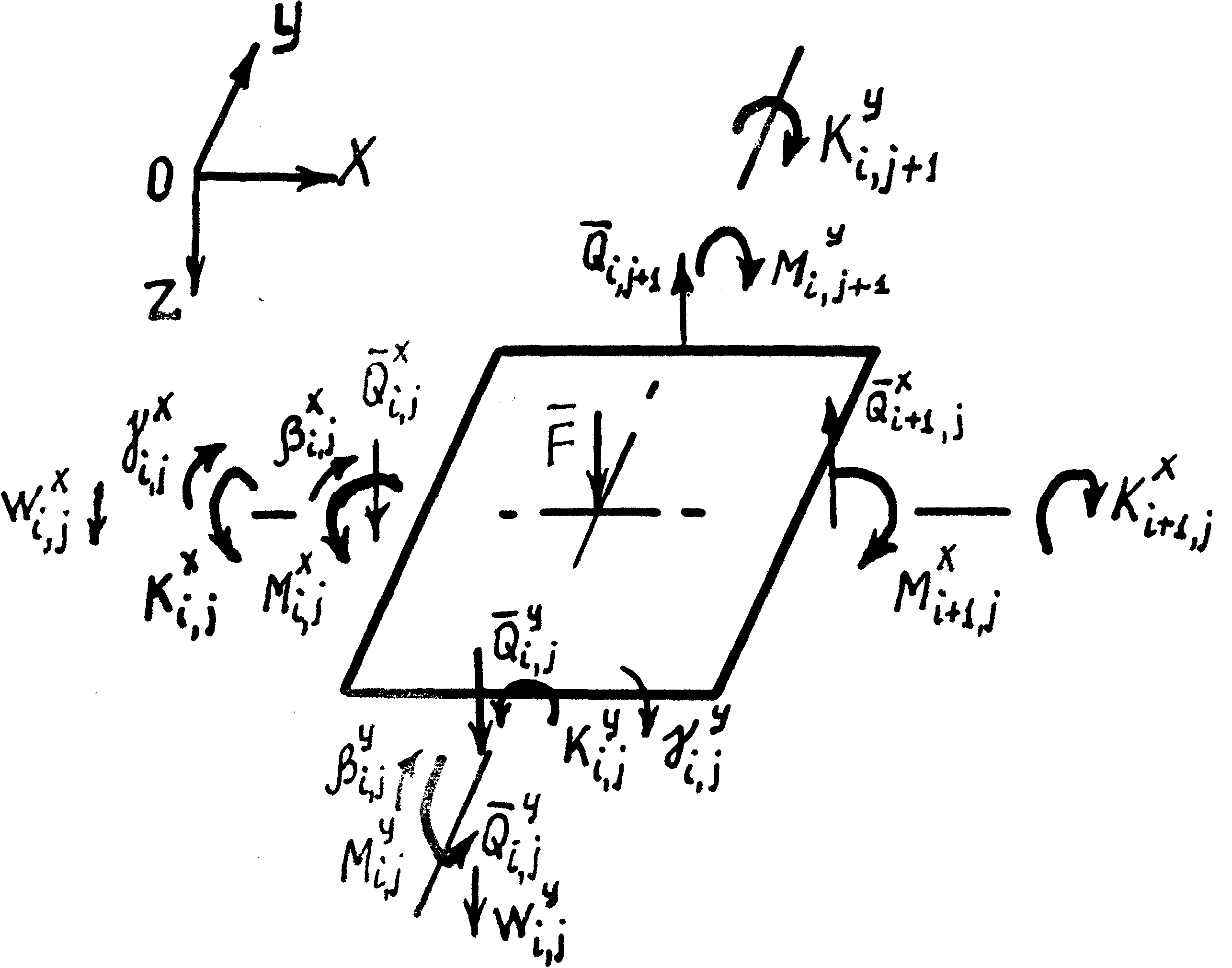
Рисунок 4.2 - Усилия и перемещения на краях выделенного

элемента пластины

Для составления алгоритма метода механической прогонки будем пользоваться следующими уравнениями для выделенного элемента. Уравнениями статического равновесия:

; (4.1)

; (4.2)

. (4.3)

Здесь распределённая нагрузка q для малого элемента с достаточной степенью точности заменена сосредоточенной силой в центре элемента: (4.4)

Как показали экспериментально-теоретические исследования [28, 83] моделирование распределённой нагрузки эквивалентной системой дискретных сил достаточно точно обеспечивается для элементов оболочек при числе сил 8.

Физические уравнения, полученные на основе закона Гука и гипотезы прямых нормалей для элемента пластины [24]

; (4.5)

; (4.6)

; (4.7)

. (4.8)

Где: Е- модуль Юнга ; , - моменты инерции на изгиб ; - коэффициент Пуассона ; ; -момент инерции на кручение ; - малоизменяемый коэффициент [97] при 10.

В дальнейшем предполагается для каждого элемента задавать разные значения нагрузок F, модуля E, геометрических размеров. Это позволит решать задачи несущей способности конструкций с учётом теплового и динамического нагружения, анизотропии свойств [98,99,100,101].

Уравнения совместности деформаций используем в форме метода перекрёстных связей, развитие которого получило в работе [24]. В центре элемента перемещения ( ) и углы поворота ( ) равны, если каждый элемент рассматривать как окончание балки, идущей по оси Х с одной стороны и окончание балки, идущей по оси У с другой стороны (рисунок 4.З).

; (4.9)

; (4.10)

(4.11)

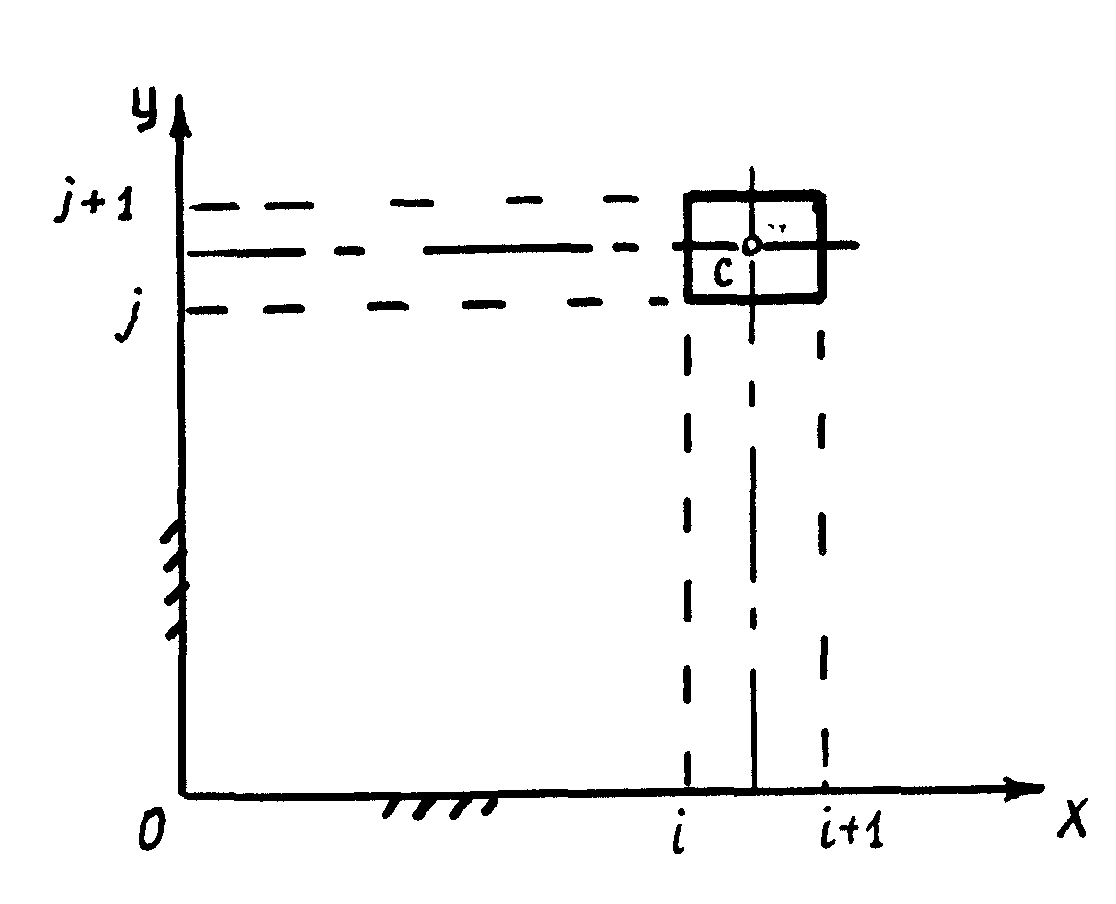
Рисунок 4.3 – Схема расположения элемента на перекрестных связях

Углы поворота и перемещения в центре определим интегрированием упругой срединной линии элемента. Интегрирование проводим с использованием производных в соотношениях (4.5) - (4.6), отдельно двигаясь по оси X от левого сечения направо к центру и по оси У от нижнего сечения вверх к центру элемента (рисунок 4.2). Получим. с учётом (4.9 – 4.11)

; (4.12)

(4.13) 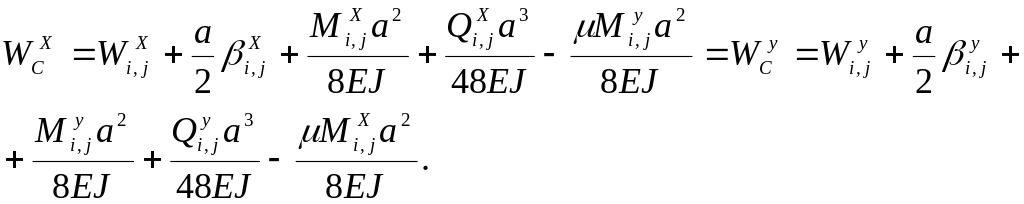(4.14)

Условия на границе элемента зависят от параметров предыдущих элементов.

Прогонка по механическим параметрам начинается с граничных условий, где для жёстко заделанной пластины [94]

; (4.15)

; (4.16)

Например, начиная с левого нижнего элемента пластины, выразим : из системы (4.12) - (4.13) через (рисунок 4.4). В последующем параметры всех элементов будем выражать через неизвестные силовые факторы на левой границе пластины и силовые факторы на верхней границе пластины . Прогонку проводим снизу вверх по каждой вертикальной полосе и, выразив параметры последнего верхнего элемента, переходим к следующей вертикальной полосе элементов слева направо.

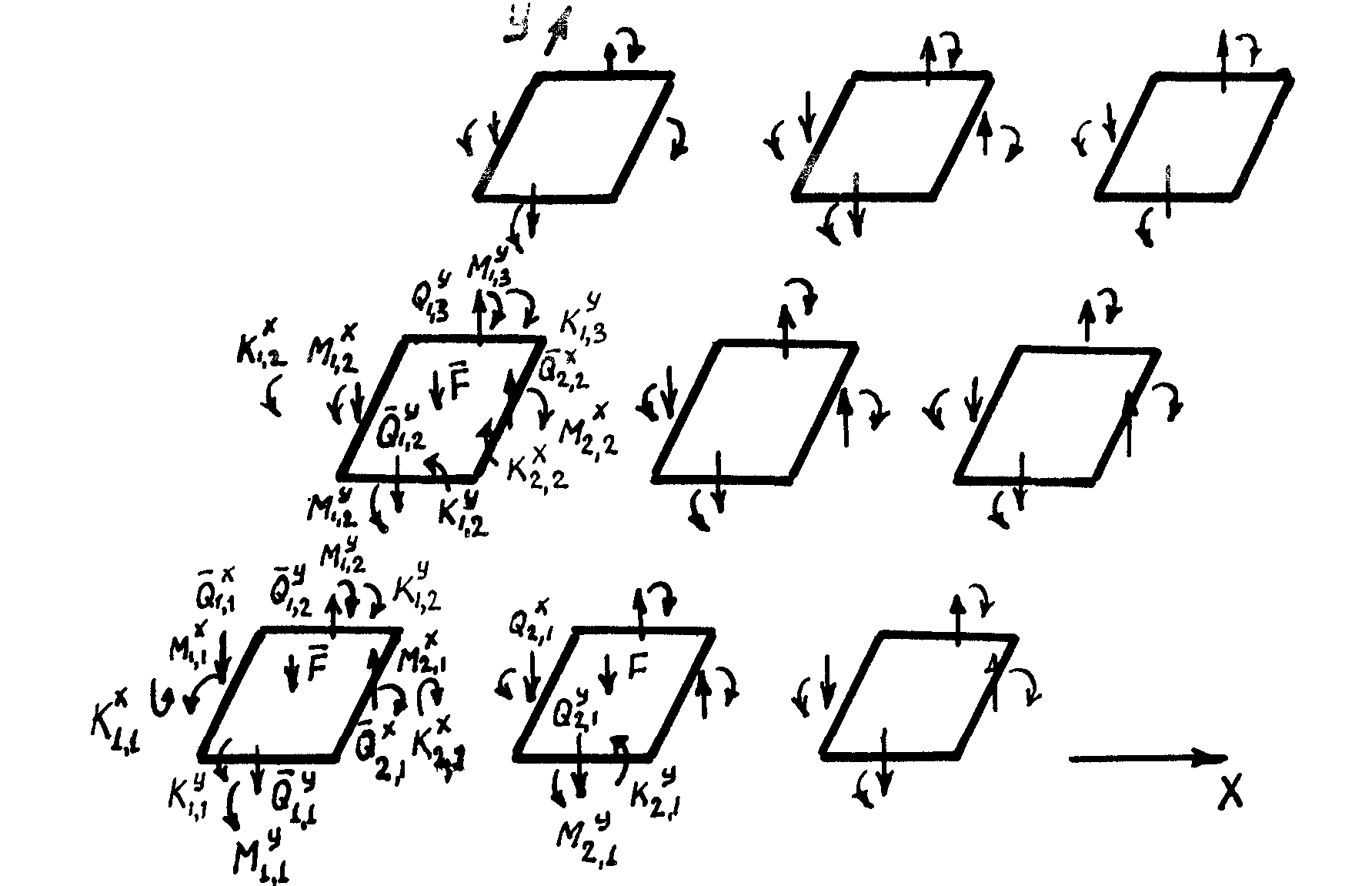
Рисунок 4.4 – Схема расчленения пластины на элементы с обозначением индексов силовых факторов на краях для составления алгоритма прогонки

При рассмотрении последующих элементов начальные условия на их границе определяют интегрированием упругой линии элемента по оси y

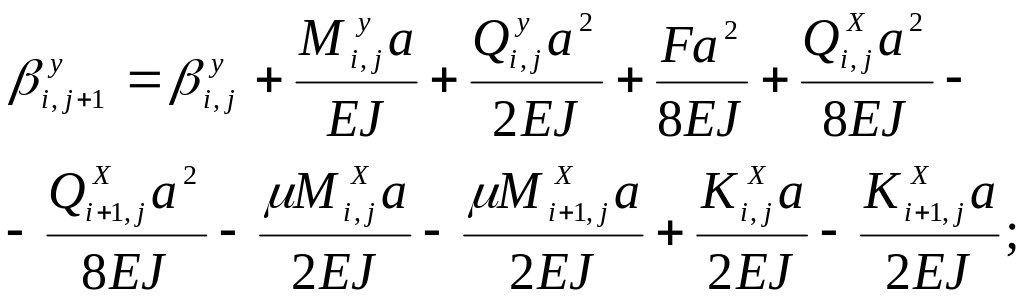(4.17)

; (4.18)

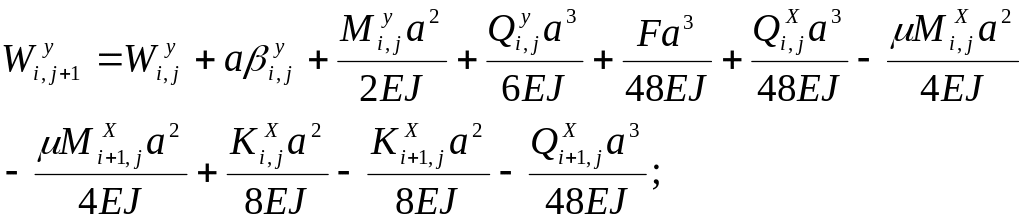(4.19)

и по оси X

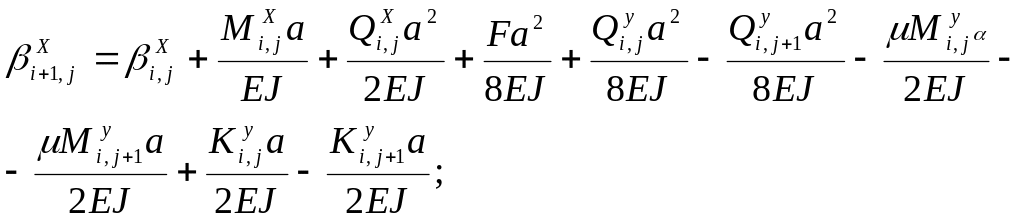(4.20)

(4.21)

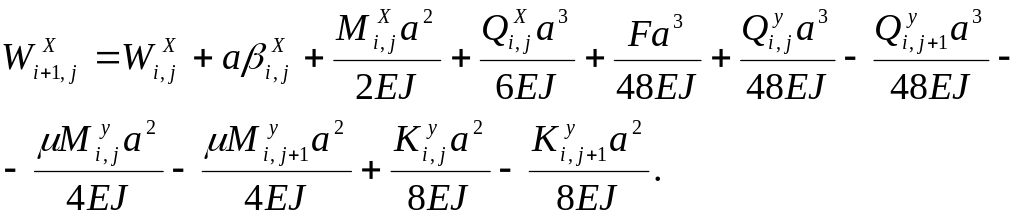(4.22)

Центральной процедурой прогонки является, определение для любого элемента с номером ( i , j ) силовых факторов на верхней границе (рисунок 4.2) через левые боковые силовые факторы следующего верхнего элемента с номером ( i , j+1 )- . Для этого из системы уравнений (4.1)- (4.3) найдём правые боковые силовые факторы у элемента с номером ( i , j ) в зависимости от остальных силовых факторов. Подставим их в систему (4.17) - (4.19). Далее составим уравнения совместности деформаций (4.12) - (4.14) для следующего вертикального элемента с номером ( i , j+1 ), подставив туда начальные условия из системы (4.17)-(4.19) предыдущего элемента.