Теорема

Если подынтегральная функция непрерывна, то производная определенного интеграла с переменным верхним переделом существует и равна значению подынтегральной функции для этого предела, т.е.

Ф’(х) = ƒ(х).

Доказательство.

Аргументу х функции придадим приращение Δх такое, что [a, b], ему соответствует приращение функции

Применяя формулу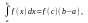 получаем 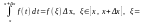= х + θΔх, 0< θ<1.

Итак, ΔФ = ƒ(ξ)Δх, откуда

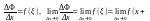θΔх) = ƒ(х), т.е.

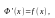или

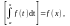
что и требовалось доказать.

Следствие. Определенный интеграл верхним пределом является одной из первообразных для непрерывной подынтегральной функции. Другими словами, для любой непрерывной на промежутке функции существует первообразная.

Формула Ньютона – Лейбница.

Формула Ньютона – Лейбница связывает неопределенный и определенный интегралы.

Если функция y=f(x) непрерывна на отрезке [a,b] ,а функция F(x)—какая-л. ее первообразная (т.е. F’(x)=f(x)), то

27.Замена переменной и интегрирование по частям в определенном интеграле. Метод замены переменной

Пусть функция у = f(х) непрерывна на отрезке [a, b], а функция x=φ(t), определена на отрезке [α, β] и имеют на нем непрерывную производную, причем φ (α) = а, φ (β) = b и для всех . Тогда

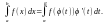
Метод интегрирования по частям

Если функции u = u(x), v = v(x) имеют непрерывные производные на отрезке [a, b], то справедлива формула

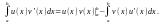Доказательство.

Поскольку функция u(x)v(x) – первообразная для функции u’(x)v(x) + u(x)v’(x), то

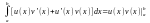
откуда и следует формула которую можно записать в виде

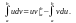
28.Площадь плоской фигуры. Объем тела вращения.

площадь S криволинейной трапеции abAB, ограниченной кривой y=f(x), f(x)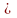 0

о

y

сью Ox и двумя прямыми x=a x=b, вычисляется по формуле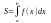

y=f(x)

а

b

x

A

B

Е

y

сли плоская фигура ABCD ограничена прямыми x=a, x=b(a<b) и кривыми y=f(x) y=φ(x), причем φ(x)≤ f(x), a≤x≤b,то ее площадь вычисляется по формуле

x

A

B

C

D

y=φ(x)

y=f(x)

Объем тела, образованного вращением кривой y = f(x), ограниченной прямыми х = а, x = b при a < x < b вокруг оси Ох, вычисляется по формуле:

Объем тела, образованного вашей кривой у = φ(у), ограниченной прямыми y = c, y = d при c < y < d вокруг оси Oy, вычисляется по формуле:

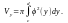
59.Дифференциальные уравнения (основные понятия)

Дифференциальным уравнением называется уравнение относительно неизвестной ф-ии и ее производных различных порядков. Порядком дифференциального урав.назыв-ся порядок старшей производной ,входящей в это уравнение.

Если искомая ф-ия зависит от одной переменной, то соответствующее диф. урав- ие назыв. обыкновенным . Если искомая ф-ция зависит от нескольких переменных , то соответсв-ее диф. уравнение назыв. Уравнением с частными производными .Обыкновенными диф-ое уравн.n-ого порядка в общем виде можно записать так:

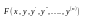=0 (1)

Где x-независимая переменная ; y=y(x) искомая ф-ия переменной 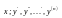-ее производные; -заданная ф-ия своих аргументов .Отметим ,что ф-ия может не содержать некоторых своих аргументов, но непременно должна зависеть от 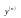(когда речь идет об уравнениях n-ого порядка).

Если уравнение (1) разрешимо относительно производной n-ого порядка, то его можно представить в виде .(2)

Ф-ия 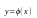, определ. и непрерывно диф-ая n раз в интервале (a,b) назыв. решением диф-ого уравнения (1)в этом интервале ,если она обращает указанное уравнение в тождество, т.е.

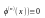
Для всех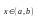

График решения диф-ого урав. n-ого порядка назыв. интегральной линией (или интегральной кривой).

Задача Коши для диф-ого урав. n-ого порядка состоит в следующем:найти решение y=y(x) уравнения (1),удовлетворяющее условиям

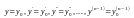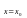при (3)

Где -заданные числа назыв. начальными данными решения.

Равенства (3),которые назыв. начальными условиями ,можно записать в таком виде:

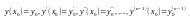
Условия существования в единственности решения задач Коши для уравнения (2) определ. след-ей теоремой ,приводимой здесь без доказательства.

Теорема 1

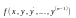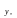
Если в уравнении функция и ее частные производные по 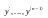непрерывны в некоторой замкнутой области G,определ неравенствами

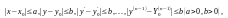и ,следовательно, ограничены в ней ,т.е

.

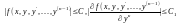(k=0,1,2, … n-1;

Где C>0, ) ,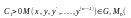

То существ. единственное решение y=y(x) данного уравн., удовлетворяющее условиям 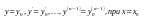.Это решение определено и непрерывно вместе с производными до порядка n включительно в промежутке где

h= min

Общим решением диф-ого урав. n-ого порядка (1)назыв. ф-ия

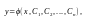(4)

Обладающая след. свойствами:1)при любых значениях произвольных постоянных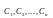 она обращает урав. (1)в тождество ;2)знач. постоянных можно подобрать так,чтобы она удовлетворяла условиям (3)

Частным решением диф-ого уравнения n-ого порядка называется решение ,получ-ся из общего решения (4)при фиксированных значениях произвольных постоянных, т. е.ф-ия

Где 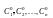-некоторые числа.

Решение диф-огоуравн.n-ого порядка, в каждой точке которого нарушается единственность решения задачи Коши, называется особым.

Общим интегралом диф-ого уравнения n-ого порядка называется соотношение вида

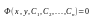(5)

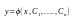
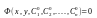Неявно определ-ее общее решение этого уравнения. Частным интегралом диф. урав-я n-ого порядка назыв. соотношение , полученное из общего интеграла путем фиксирования значений 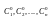произвольных постоянных.