
- •6.Уравнение прямой с угловым коэффициентом
- •30.Угол между 2-мя прямыми.
- •18.Скалярные и векторные величины.
- •3. Проекция вектора на ось
- •8.Уравнение прямой в пространстве
- •4. Линейная зависимость векторов. Базис. Разложение вектора по данному базису.
- •1. Матрица. Операции над матрицами.
- •2.Операции над матрицами:
- •2. Система линейных алгебраических уравнений относительно n неизвестных. Решение системы методом Гаусса. Понятие базисного решения.
- •9.Числовая последовательность. Определение предела числовой последовательности.
- •14. Производная ф-ции. Смысл.
- •16. Произв. Сложной и обр. Ф-ции.
- •19.Первообразная функции. Неопределённый интеграл. Основные свойства неопределённого интеграла
- •21,22.Замена переменной (подстановка) в неопределённом интеграле. Интегрирование по частям.
- •23.Универсальная тригонометрическая подстановка.
- •25.Определённый интеграл. Его свойства.
- •Теорема
- •Формула Ньютона – Лейбница связывает неопределенный и определенный интегралы.
- •27.Замена переменной и интегрирование по частям в определенном интеграле. Метод замены переменной
- •28.Площадь плоской фигуры. Объем тела вращения.
- •59.Дифференциальные уравнения (основные понятия)
- •60. Дифференциальные ур-я 1-го порядка с разделяющимися переменными:
- •62. Линейные дифф-е ур-я 1-го порядка:
- •64. Линейные дифференциальные ур-я 2-го порядка с постоянными коэффициентами:
- •38.Знакочередующиеся ряды.Признак Лейбница.
- •40,42..Понятие степенного ряда .Область сходимости степенного ряда
- •43. Ряды Тейлора и Маклорена.
- •35. Линейная комбинация рядов
- •36. Сравнение,даламбера,интегральный признак, лейбница.
- •40. Доказательство расходимости Предположим, что гармонический ряд сходится к сумме :
- •44. Разложение основных элементарных функций.
- •47. Функции нескольких переменных
- •7°. Важное геометрическое свойство. Равен площади области d (Это свойство, как уже отмечалось ранее, непосредственно вытекает из определения интегрируемости
- •65. Решение дифференциальных уравнений с помощью степенных рядов. С помощью степенных рядов возможно интегрировать дифференциальные уравнения.
- •15. Производная суммы (разности) функций
- •63. Теорема (о структуре общего решения лнду):
6.Уравнение прямой с угловым коэффициентом

![]()
![]()
![]()
![]()
Общее уравнение прямой.


Ур-ние прямой, проходящей через 2 точки. Ур-ние прямой в отрезках.

![]()
![]()

![]()
![]()
30.Угол между 2-мя прямыми.
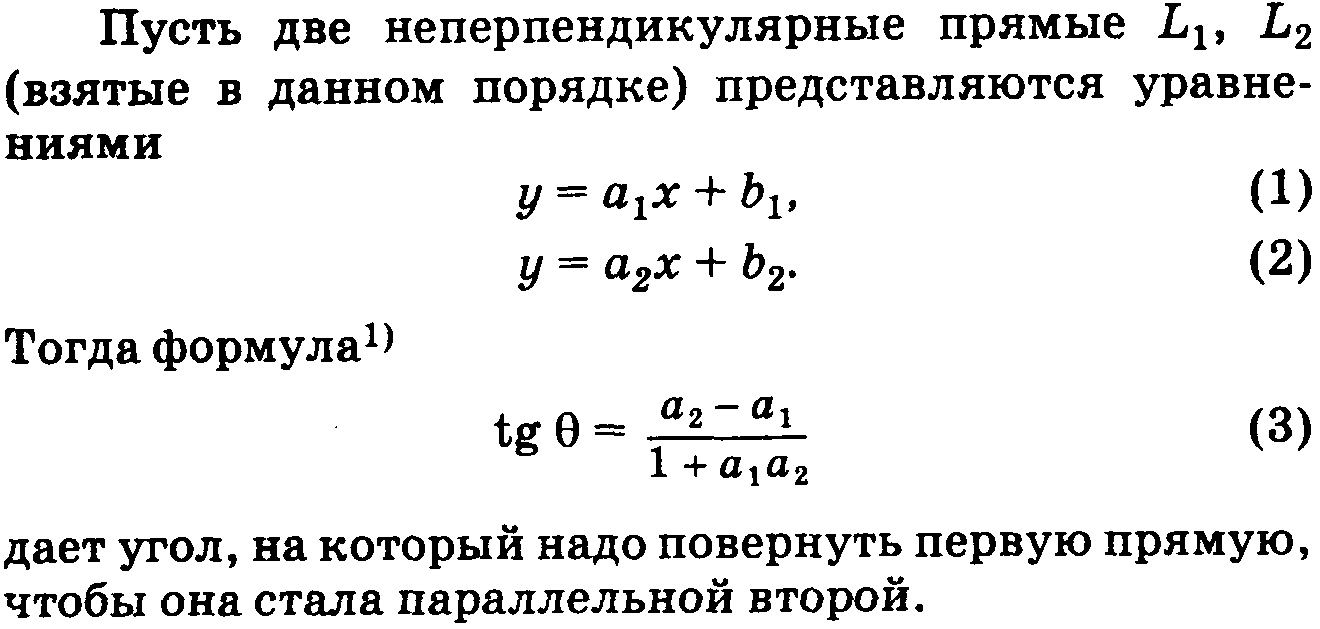


![]()

18.Скалярные и векторные величины.
![]()
Скалярное произведение 2-ух векторов и его свойства
Скалярным поизведением ā и đ назыв число ā*đ равное |ā|*|đ|*cos(ā;đ), где (ā;đ) – наименьший угол между направл ā и đ.
Свойства:
ā*đ=đ*ā
(λ*ā)*đ=ā*(λ*đ)=λ*(ā*đ)
ā*(đ+ē)=ā*đ+ā*ē
ā*đ=|ā|*ПРāđ=|đ|*ПРđā
ā*ā=ā2=|ā|2
Если ā и đ ненулевые, то ā*đ=0 (ā┴đ)
Пусть в отронормиров базисе
ā=(x1,y1,z1)
đ=( x2,y2,z2)
ā *đ=
x1*
x2+
y1*
y2+
z1*z2
*đ=
x1*
x2+
y1*
y2+
z1*z2
|ā|=
3. Проекция вектора на ось
Выражение «проекция вектора АВ на ось ОХ» употребляется в двух разных смыслах: геометрическом и алгебраическом (арифметическом).
1. Проекцией (геометрической) вектора АВ на ось ОХ называется вектор А'В' , начало которого А' есть проекция начала А на ось ОХ, а конец В' — проекция конца В на ту же ось.
Обозначение: Прох АВ или, короче, Пр АВ . Если ось ОХ задана вектором с, то вектор А'В' называется также проекцией вектора АВ на направление вектора с и обозначается Прс АВ .
Геометрическая проекция вектора на ось ОХ называется также компонентой вектора по оси ОХ.
2. Проекцией (алгебраической) вектора АВ на ось ОХ (или на направление вектора с) называется длина вектора А'В', взятая со знаком + или -, смотря по тому, имеет ли вектор А'В' то же направление, что и ось ОХ (вектор с), или противоположное.
Обозначение: прох АВ или прс АВ .
Замечание. Геометрическая проекция (компонента) вектора есть вектор, а алгебраическая проекция вектора есть число.
Основные теоремы о проекциях вектора
Теорема 1. Проекция суммы векторов на какую-либо ось равна сумме проекций слагаемых векторов на ту же ось.
Теорема справедлива при обоих смыслах термина «проекция вектора» и при любом числе слагаемых; так, при трех слагаемых
Пр (а1+ а2 + а3) = Пр а1 + Пр а2 + Пр а3 (1) и
np(а1 + а2 + а3) = пра1 + пра2 + пра3. (2)
Теорема 2. Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
пр. b = |b| cos (а^b). (3)
8.Уравнение прямой в пространстве
1.Кононическое
ур-ние прямой(по точке и направленному
вектору): Рассмотрим М.
Для того,
чтобы М принадлежала прямой нужно
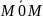 ⃓⃓
⃓⃓
 М0М=(x-x0,
y-y0,
z-z0)
М0М=(x-x0,
y-y0,
z-z0) t=
t=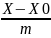 =
= =
= .
Знаменатель может превращаться в
0(символическая запись)
.
Знаменатель может превращаться в
0(символическая запись)
2.Параметрическое уравнение:
 =>
=>
3.Ур-ние по 2 точкам: М Є прямой, когда М1М2⃓⃓ М1М. М1М2=(x2-x1, y2-y1, z2-z1), М1М=(x-x1, y-y1, z-z1)
 =
= =
=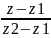 .
.
4.
Общее ур-ние прямой:
 ,
n1 не
⃓⃓
n2,
,
n1 не
⃓⃓
n2,
 ⊥
⊥ 1,
⊥
2
1,
⊥
2
Угол
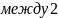 прямыми:
прямыми:
 .
.
⃓⃓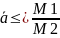 =
=
⊥ a1×a2=0m1×m2+n1×n2+p1×p2.
4. Линейная зависимость векторов. Базис. Разложение вектора по данному базису.
Любые
колениарные векторы,3 комплонарных
вектора,4-и более векторов в трёхмерном
пространстве всегда линейнозависимы.
3 упорядоченных линейно-независимых
вектора
 1
1
 2
3
наз. базисом. Упорядоченная тройка
некомплонарных векторов всегда образует
базис трёхмерного пространства.
Неколинеарная пара упорядоченных
векторов образует базис двухмерного
пространства. В n-мерном пространстве
любая упорядоченная линейно-независимая
система n-векторов образует базис. Любой
вектор
можно разложить в виде линейной
комбинации базисных векторов.
=x
1+y
2+z
3,
где x,y,z наз. координатами вектора
в базисе
1,
2,
3.Базис
наз. ортонормированным, если его векторы
взаимноперпендикулярны и имеют единую
длину. Такой базис обозначают
2
3
наз. базисом. Упорядоченная тройка
некомплонарных векторов всегда образует
базис трёхмерного пространства.
Неколинеарная пара упорядоченных
векторов образует базис двухмерного
пространства. В n-мерном пространстве
любая упорядоченная линейно-независимая
система n-векторов образует базис. Любой
вектор
можно разложить в виде линейной
комбинации базисных векторов.
=x
1+y
2+z
3,
где x,y,z наз. координатами вектора
в базисе
1,
2,
3.Базис
наз. ортонормированным, если его векторы
взаимноперпендикулярны и имеют единую
длину. Такой базис обозначают
 ,
,
 ,
,
 .
.
