40. Доказательство расходимости Предположим, что гармонический ряд сходится к сумме :

Тогда, перегруппируя дроби, получим:

Вынесем из второй скобки  :

Заменим вторую скобку на  :

Перенесём   в левую часть:

Подставим обратно вместо   сумму ряда:

Это равенство, очевидно, неверно, так как единица больше одной второй, одна треть больше одной четвёртой, и так далее. Таким образом, наше предположение осходимости ряда ошибочно, и ряд расходится.

44. Разложение основных элементарных функций.

Теорема 2.1. Если функция f(x) определена и  имеет производные сколь угодно высоких порядков и существует  постоянная, такая, что при лю­бых х и п удовлетворяет неравенству   то функция f(x) разлагается в ряд Тейлора (1.2) при любом x₀.

Приведем без доказательства следующие разложения элементарных функций в ряд Маклорена

 

 

 

это разложение имеет место при любом натуральном значении  и любом значении x, если число   не является натуральным, то данное равенство справедливо лишь при –1<x<1;

 

 

 

46. Тригонометрическим рядом Фурье функции   называют функциональный ряд вида

где

47. Функции нескольких переменных

1).Определение. Если каждой паре (x,y) значений двух независимых переменных из области W ставится определенное значение z, то говорят, что z есть функция двух переменных (x,y).

z=f(x,y)

2).Геометрическое изображение функции двух переменных - поверхность.

3).Частное и полное приращение функции.

Полное приращение функции

Dz=f(x+Dx, y+Dy)-f(x,y)

Частное приращение функции

Dx z=f(x+Dx)-f(x,y)

Dy z=f(x,y+Dy)-f(x,y)

Вообще, полное приращение функции не равно сумме частных приращений. Пример. z=xy.

Dx z=(x+Dx)y-xy=yDx

Dy z=x(y+Dy)-xy=xDy

Dz=(x+Dx)(y+Dy)-xy=yDx+xDy+DyDx № Dy z+Dx z.

4).Непрерывность функции нескольких переменных

Предел функции.

Пусть z=f(x,y) определена в некоторой окрестности A(x0,y0).

Определение. Постоянное число b называют пределом z=f(x,y) при P(x,y) стремящемся к A, если для любого e > 0 можно указать такое значение d > 0, что для всех x, удовлетворяющих неравенству |AP| < d, имеет место неравенство |f(x,y)-b| < e.

5).Непрерывная функция

6).Частные производные

48,49.

Пусть функция Z=f(M) определена на некотором множестве {M} и точка M₀ {M} или M₀ {M}, но обладает тем свойством, что в любой δ-окрестности этой точки содержится хотя бы одна точка множества {M}, отличная от M₀.

ОПРЕДЕЛЕНИЕ: Число А называется пределом функции Z=f(M) в точке M₀, если функция Z=f(M) определена в окрестности точки M₀ и для любого ε>0, δ>0 такое что при |M₀M|<δ, выполняется неравенство |f(M)-A|<ε.

обозначение: 

ОПРЕДЕЛЕНИЕ: Функция Z=f(M) называется непрерывной в точке M₀, если предел функции в этой точке существует и равен значению функции в этой точке, т.е.

50.   Пусть f(x, y) — функция двух переменных x, y, определена в некоторой окрестности точки (x₀, y₀). Если существует конечный предел  ,то функция f(x, y) имеет в точке (x₀, y₀) частную производную по переменной x. Аналогично определяется частная производная функции f(x₁, x₂, …, x_n) по переменной x_i : Обозначают: ,

50. Функция двух переменных обычно записывается как  , при этом переменные  ,   называются независимыми переменными или аргументами.

Пример:   – функция двух переменных.

1) Когда мы находим частную производную  , переменная   считается константой.

2) Когда мы находим частную производную  , переменная   считается константой.

3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной ( ,   либо какой-нибудь другой), по которой ведется дифференцирование.

51. В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.

Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.

ГРАДИЕНТ ФУНКЦИИ

и = f(x, у, z), заданной в некоторой обл. пространства (X Y Z), есть вектор с проекциями   обозначаемый символами: grad  где i, j, k — координатные орты. Г. ф. — есть функция точки (х, у, z), т. е. он образует векторное поле. Производная в направлении Г. ф. в данной точке достигает наибольшего значения и равна: 

55. Экстремумы функции двух переменных

Теорема (необходимое условие экстремума). В точке экстремума функции нескольких переменных каждая ее частная производная либо равна нулю, либо не существует.

Точки, в которых выполнены эти условия, называются критическими.

56. Достаточные условия экстремума функции двух переменных

Т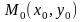 еорема. Пусть функция z=f(x,y) определена и имеет непрерывные частные производные второго порядка в некоторой окрестности точки

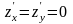
в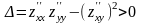 которой . Если при этом в этой точке выполнено условие ,

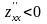
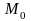
т о точка является точкой экстремума функции, причем точкой максимума, если , и точкой минимума, если

.

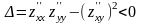Если же в этой точке

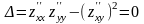, то экстремума в точке нет.

В том случае, если

В точке , теорема ответа не дает.

5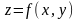 2. Определение дифференцируемой функции

Функция называется дифференцируемой в точке М(х,у), если ее полное приращение можно представить в виде

,

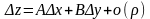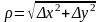где Δx и Δy -произвольные приращения аргументов х и у в некоторой окрестности точки М(х,у), А и В –постоянные, независящие от Δx и Δy , o(ρ)-бесконечно малая более высокого порядка, чем

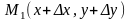
-расстояние между М(х,у) и

О пределение дифференциала Главная линейная относительно Δx и Δy часть полного приращения функции называется полным дифференциалом этой функции и обозначается dz или df(x,y) . Таким образом,

Е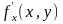 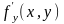сли функция дифференцируема в точке М(х,у),то она имеет в этой точке частные производные и , причем

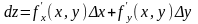=А, а =В Таким образом, .

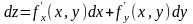
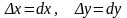Если положить , то

53. Пусть задана функция f(x, y). Тогда каждая из ее частных производных(если они, конечно, существуют)   и  , которые называются также частными производными первого порядка, снова являются функцией независимых переменных x, y и может, следовательно также иметь частные производные. Частная производная   обозначается через   или  , а   через   или  . Таким образом,

, 

и, аналогично,

,  .

Производные   и   называются частными производными второго порядка. Определение:Частной производной второго порядка от функции z=f(x;y) дифференцируемой в области D,называется первая производная от соответствующей частной производной. Рассматривая частные производные от них, получим всевозможные частные производные третьего порядка:  ,  ,   и т. д.

57. Метод наименьших квадратов— один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.

Необходимо отметить, что собственно методом наименьших квадратов можно назвать метод решения задачи в любой области, если решение заключается или удовлетворяет некоторому критерию минимизации суммы квадратов некоторых функций от искомых переменных.

58. ∫∫M f(x1;x2)dx1dx2 и называется двойным интегралом на множестве М.

Свойства двойного интеграла (и их вывод) аналогичны соответствующим свойствам однократного определенного интеграла.

     1°. Аддитивность. Если функция f(x, y) интегрируема в области D и если область D при помощи кривой Г площади нуль разбивается на две связные и не имеющие общих внутренних точек области D₁ и D₂, то функция f(x, y) интегрируема в каждой из областей D₁ и D₂,

     2°. Линейное свойство. Если функции f(x, y) и g(x, y) интегрируемы в области D, а α и β - любые вещественные числа, то функция [α · f(x, y) + β · g(x, y)] также интегрируема в области D,

     3°. Если функции f(x, y) и g(x, y) интегрируемы в области D, то и произведение этих функций интегрируемо в D.

     4°. Если функции f(x, y) и g(x, y) обе интегрируемы в области D и всюду в этой области f(x, y) ≤ g(x, y), то

     5°. Если функция f(x, y) интегрируема в области D, то и функция |f(x, y)| интегрируема в области D, причем

     6°. Теорема о среднем значении. Если обе функции f(x, y) и g(x, y) интегрируемы в области D, функция g(x, y) неотрицательна (неположительна) всюду в этой области, M и m - точная верхняя и точная нижняя грани функции f(x, y) в области D, то найдется число μ, удовлетворяющее неравенству m ≤ μ ≤ M и такое, что справедлива формула