60. Дифференциальные ур-я 1-го порядка с разделяющимися переменными:

Дифференциальным уравнением 1-го порядка с разделяющимися переменными называется уравнение вида: P(x)dx+Q(y)dy=0 (1). Его общим интегралом будет: (2). Уравнение вида: M₁(x)·N₁(y)dx+M₂(x)·M₂(y)dy=0 (3), а также уравнение вида: y'=f₁(x)·f₂(y) (4) уравнения, которые с пом. алгебраических преобразований приводятся к ур-ям (3) или (4) наз. ур-ми с разделяющимися переменными. Рассмотрим ур-е (3). Допустим, что N₁(y)·M₂(x)≠0. Разделим обе части ур-я (3) на N₁(y)·M₂(x). Получим: ,

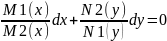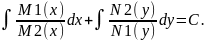Рассмотрим ур-е (4): 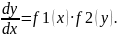Домножим обе части ур-я на dx и разделим на f₂(y) в предположении, что f₂(y)≠0.

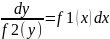
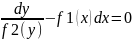
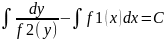– общий интеграл.

Замечание: При выводе общих интегралов ур-ий (3) и (4) сделаем нек. допущения, к-е могут привести к потере решений. Случай, когда M₁(y)·M₂(x)=0 или f₂(y)=0 необходимо рассматривать отдельно, чтобы не потерять возможных решений дифференциальных ур-ий.

62. Линейные дифф-е ур-я 1-го порядка:

Ур-е: y'+P(x)y=Q(x) (1) линейное относительно неизвестной ф-ии y и её производной y' (а также любое ур-е, с пом. алгебраических преобразований, приводящееся к виду (1) наз. неоднородным линейным дифф-ым ур-ем 1-го порядка. В случае, когда Q(x)=0 ур-е наз. однородным линейным дифф-м ур-м 1-го порядка. Ф-ии Q(x),P(x) должны быть непрерывны в нек. области, для того, чтобы выпол. услов. теоремы Коши.

Методы решения:

1.Метод вариации произвольной постоянной (метод Лангранжа):

y'+P(x)y=0

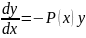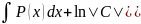
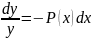ln y|=-

y=

=

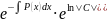
y₀=C·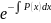

C=C(x)-частное реш. неоднородного ур-я (1)

y_н=C(x)·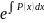

d(x)·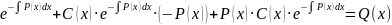

C '(x)-C(x)·P(x)+C(x)·P(x)=Q(x)·

y_н=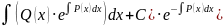

Общее реш-е неоднор. ур-я (1) имеет вид:

y=y₀+y_н=С·

2.Метод Бернулли:

Любую функцию можно представить в виде произв-я 2-х ненулевых ф-ий y(x)=U(x)·V(x)

U'V+UV'+P·UV=Q

U'V+U(V'+PV)=0=Q

V'+PV=0

V'+PV=0

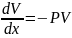
ln|V|=-

V=C· C=1

V=

U' =0

U'=Q

U=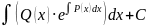

U=(

U' V+U V'+U Vtgx=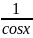

U' V+U(V'+Vtgx)=

V'+Vtgx=0

V'+Vtgx=0

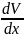+Vdx=0

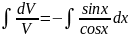
ln|V|=ln|cosx|+ln|C|

ln|V|=ln|C·cosx| C=1

V=cosx

U'cosx=

U'=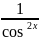

U=tgx+C

y=(tgx+C)·cosx=sinx+C·cosx

64. Линейные дифференциальные ур-я 2-го порядка с постоянными коэффициентами:

y''+py'+gy=0 (1) p, g Є R.

λ²+pλ+g=0 (2)

1) λ₁, λ₂, Є R, λ₁≠λ₂

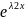Решение: y_{1= ,} y_{2= ,} y₀₌C_{1 +}C₂

2) λ_1, λ₂ Є R, λ₁₌λ₂=λ

y_{1=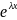 ,} y₂=x , y₀=C_{1 +}C₂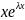

3)λ_1, λ₂ Є C, λ_1/2=α±β_i

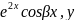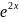y_{1= 2=} sinβx

y₀=C_{1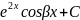 2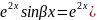 1}cosβx+C2sinβx)

Рассмотрим ур-е: y''+py'+gy=f(x) (3)

Во многих случаях правая часть ур-я (3) имеет вид: f(x)=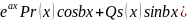 (4), где Pr(x) и Qs(x)-многочлены в степени r и s соответственно, а и в- некоторые постоянные числа.

Известно, что в этом случае частное решение y_н(х) ур-я (3) имеет аналогичную структуру правой части, т.е. частное решение в этом случае необходимо искать

у_н(х)=х^к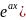 _m(x)cosbx+Q(x)sinbx) (5), где P_m(x) и Q_m(x)- многочлены степени m

m={r,s}, k=числу корней характеристического ур-я совпадающему числу z=a+b_i

f(x)=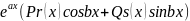

y_н=х^к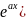 _m(x)cosbx+Q_m(x)sinbx)

m=max

k: a+b_i

64

31.Числовые ряды: если задана числовая последовательность (u_n), то выражение

u₁ + u₂ + u₃ +… + u_n +…, называется числовым рядом.

ⁿ

Если существ. lim S_n = S, где S_n = ∑ u_k = u₁ + u₂ +… + u_n −

_{n - ∞ k=1}

его n –ая частичная сумма, то ряд назыв. сходящимся (число S – сумма ряда),

в противном случае – расходящимся.

Если ряд сходится, то

lim u_n = 0

_{n - ∞} (необходимый признак сходимости)