§13. Релятивістська інваріантна форма рівнянь Максвела для зарядів і струмів у вакуумі.
Для запису рівнянь Максвела
(5.1) – (5.4) у чотиривимірній формі необхідно,
насамперед, замість тривимірних
характеристик електромагнітного
поля
і
ввести
чотиривимірні характеристики,
скориставшись для цього чотирьохвектором
потенціалу (12.7) і формулами (6.1) – (6.2):
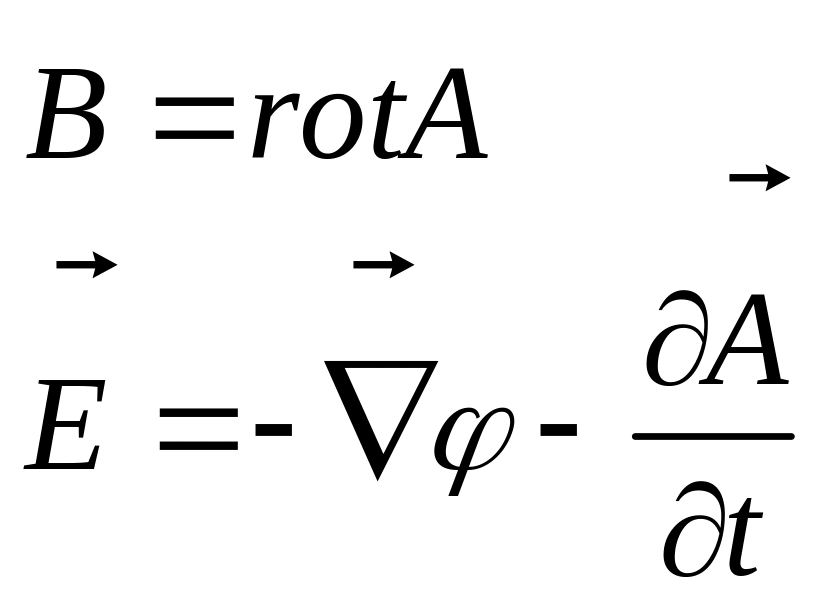(13.1)
які зв'язують потенціали і напруженості. У позначеннях (12.7):
переписуємо (13.1) так:
(13.2)
Подібність цих виразів наштовхує на думку, що компоненти векторів і можна виразити за допомогою одного чотиривимірного тензора другого рангу, а саме тензора:
,
, (13.3)
де А
- коваріантні
компоненти 4-потенціалу (12.7). З визначення
(13.3) видно, що тензор
є
антисиметричним
(
=
), тому він має тільки шість
незалежних компонентів,
що можна наочно зобразити за допомогою
матричного
його запису:
(13.4)
Явне вираження компонентів через компоненти векторів , одержуємо з порівняння (13.3) з (13.2) і наочно представляємо в матричному записі:
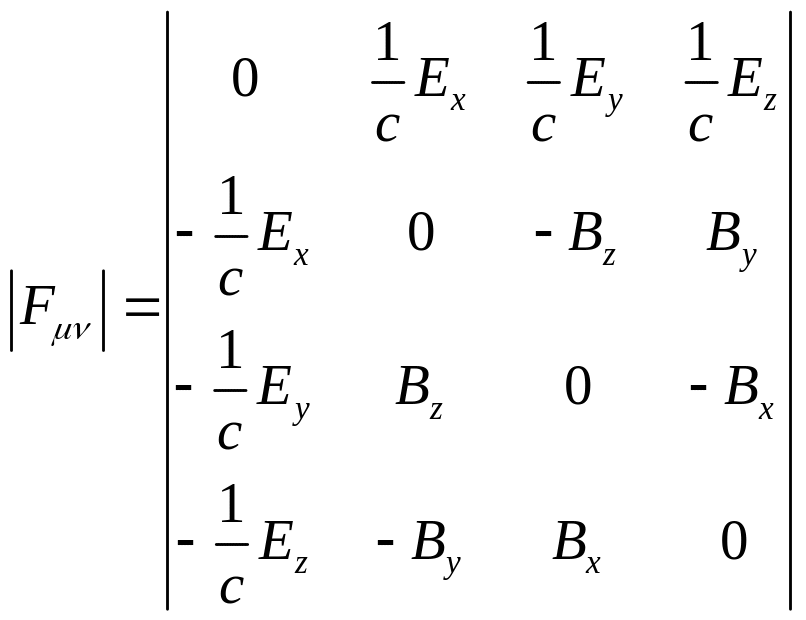(13.5)
Чотирьохтензор називається тензором електромагнітного поля це є чотиривимірна характеристика електромагнітного поля, що поєднує його тривимірні характеристики і : з (13.5) видно, що електричне і магнітне поля не є незалежними друг від друга і що вони перетворяться друг через друга при переході з однієї ІСВ до іншої відповідно до загального правила (10, …) перетворення тензорів другого рангу. Тому, навіть у випадку постійного електромагнітного поля його розподіл на електричне і магнітне поля є відносним, тобто залежним від вибору ІСВ.
Можна визначить і контраваріантні компоненти тензора електромагнітного поля:
, (13.6)
які зв'язані з коваріантними компонентами (13.3) за допомогою метричного тензора (див. §10):
(13.7)
Формули (13.5) і (13.7) дозволяють
легко знайти явний вигляд
компонентів
(наприклад,
і так далі):
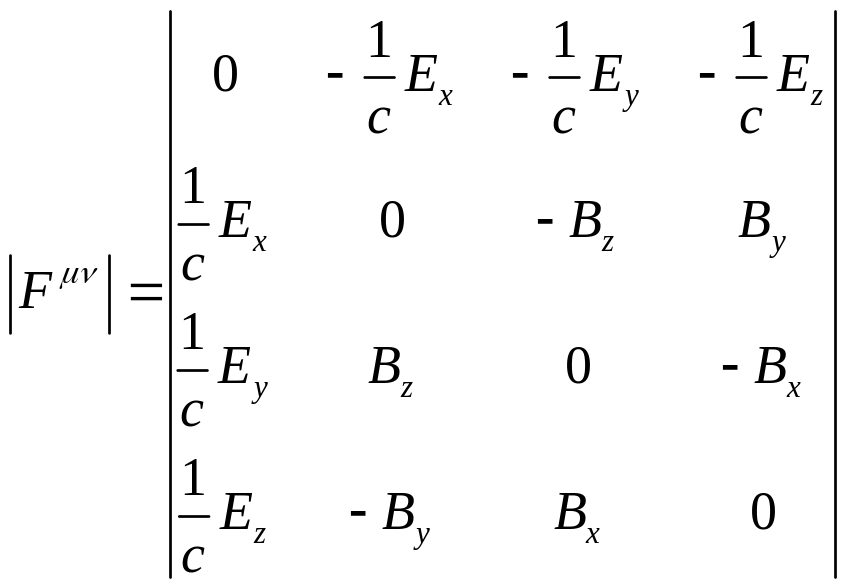(13.8)
Для наступного запису рівнянь
Максвела в чотиривимірній формі нам
буде потрібно ще визначити
тензор
, що є
дуальним
до тензора
. Для визначення математичного дуального
тензора, визначимо
спочатку так званий антисиметричний
символ (тензор) Леви-Чивити
в такий спосіб:
і для будь-яких
виконується умова:
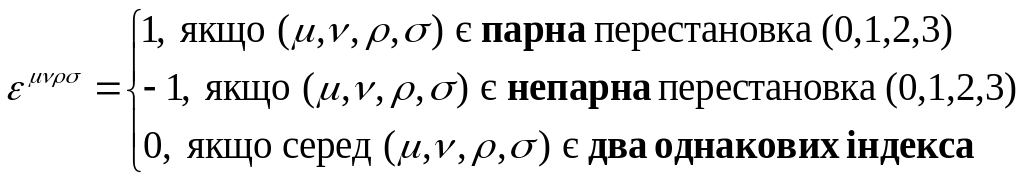(13.9)
З визначення (13.9) видно, що
є цілком
антисиметричний (по будь-якій
парі індексів) тензор четвертого рангу,
компоненти якого можуть приймати тільки
три
значення – 1, -1, і 0 (наприклад
і так далі). Цей символ Леви-Чивити
використовується для перетворення
антисиметричних
тензорів у так звані дуальні
тензори. Зокрема, тензор
,
дуальний
тензору електромагнітного
поля, визначаємо
співвідношенням:
,
(13.10)
З визначення (13.10) з
врахуванням (13.5) і (13.9) легко знайти явний
вигляд:
компонентів
(наприклад,
і так далі):
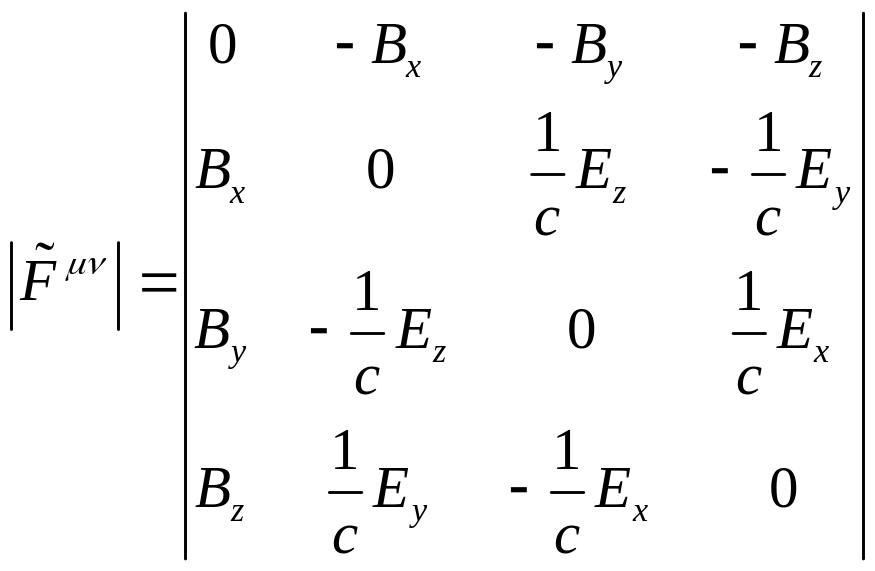(13.11)
Тензор ми будемо називати дуальним тензором електромагнітного поля. Легко переконатися в справедливості співвідношення:
(13.12)
яке є
зворотним
до співвідношення (13.10) і яке дозволяє
зробити
перехід від дуального тензора до
звичайного тензора електромагнітного
поля. Таким чином, повною
чотиривимірною характеристикою
електромагнітного
поля може служити як тензор електромагнітного
поля
(чи
)
, так і дуальний тензор
(чи
).
Тепер ми готові до одержання чотиривимірного запису рівнянь Максвела (5.1) (5.4). Спочатку представимо в чотиривимірній формі пари рівнянь (5.1) і (5.3), тобто рівняння:
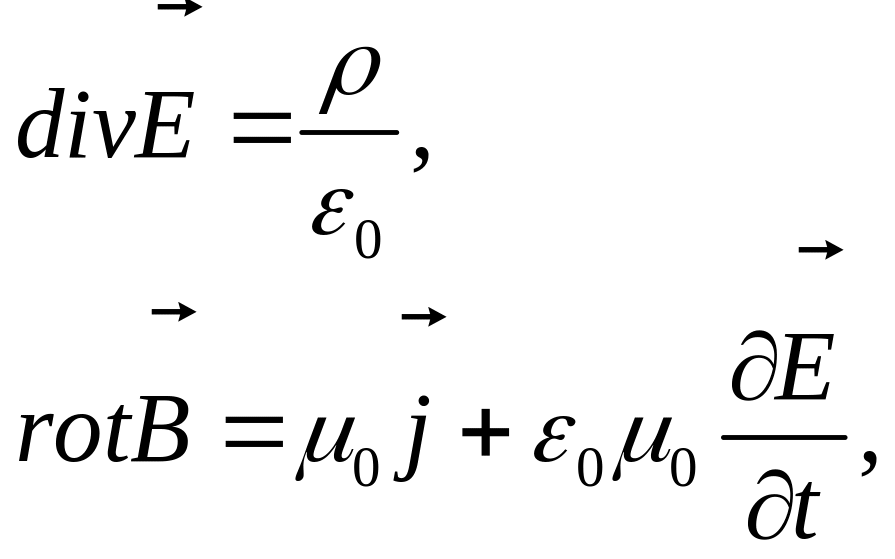(13.13)
утримуючи електричні заряди.
У декартових
координатах рівняння (13.13) мають вигляд
(врахуємо, що
):
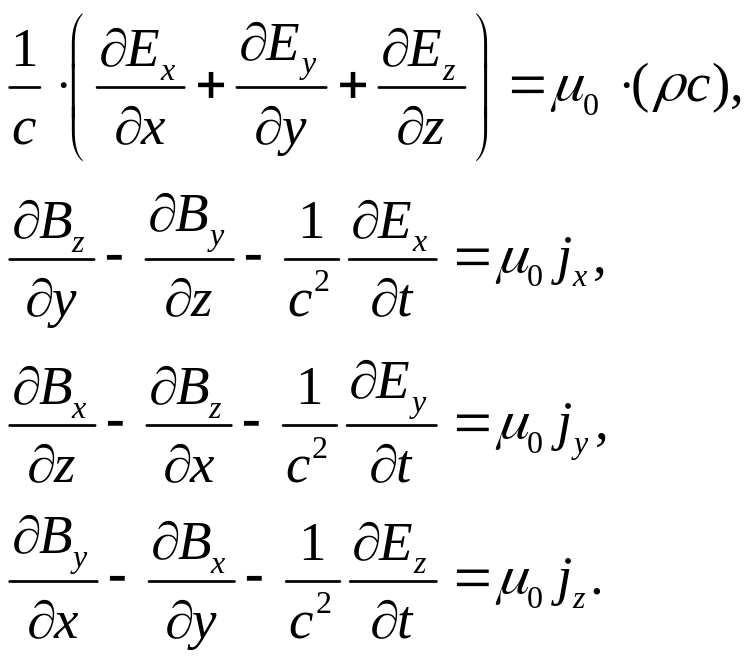
За допомогою чотиривимірних величин (12.8) і (13.8) переписуємо ці рівняння так:
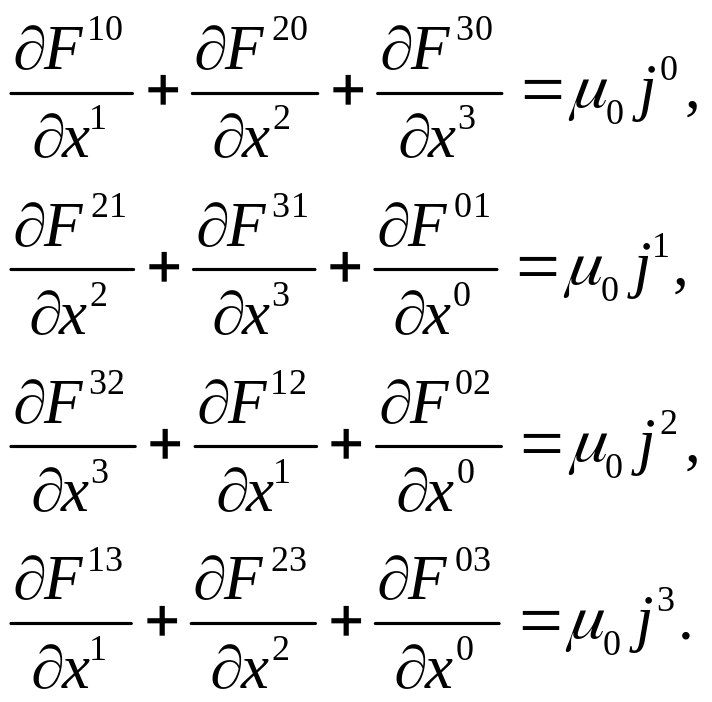
Далі, додаючи до лівої частини
першого рівняння рівний
нулю доданок
,
до лівої частини другого рівняння -
,
до лівої частини третього
,
до лівої частини четвертого
-
,
одержуємо:
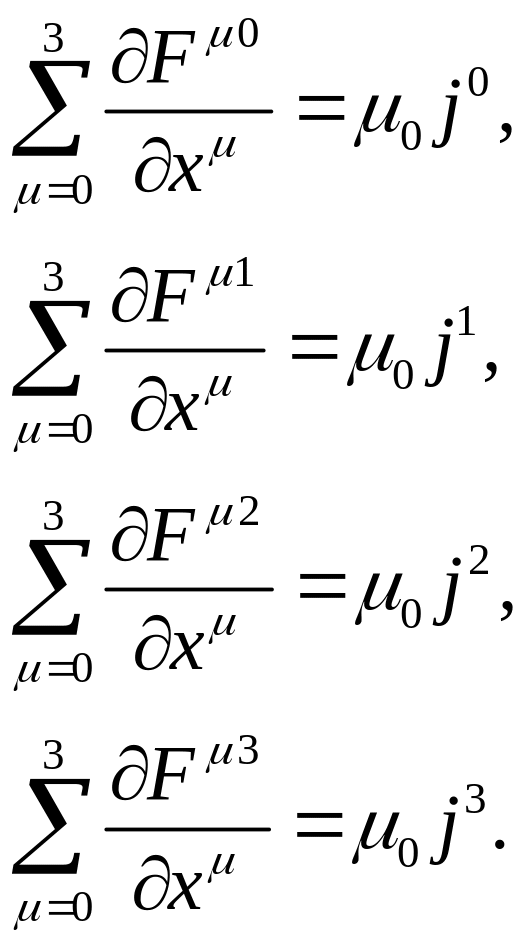(13.14)
Ці чотири рівняння можна розглядати як проекції на осі евклідової системи координат одного чотиривимірного векторного рівняння в П-Ч Минковского
(13.15)
Ліва і права частини цього рівняння перетворяться як чотирьохвектор, тому в будь-який інший ІСВ рівняння (13.15) не змінює свого вигляду:
(13.16)
Нам залишилося розглянути рівняння Максвела (5.2) і (5.4)
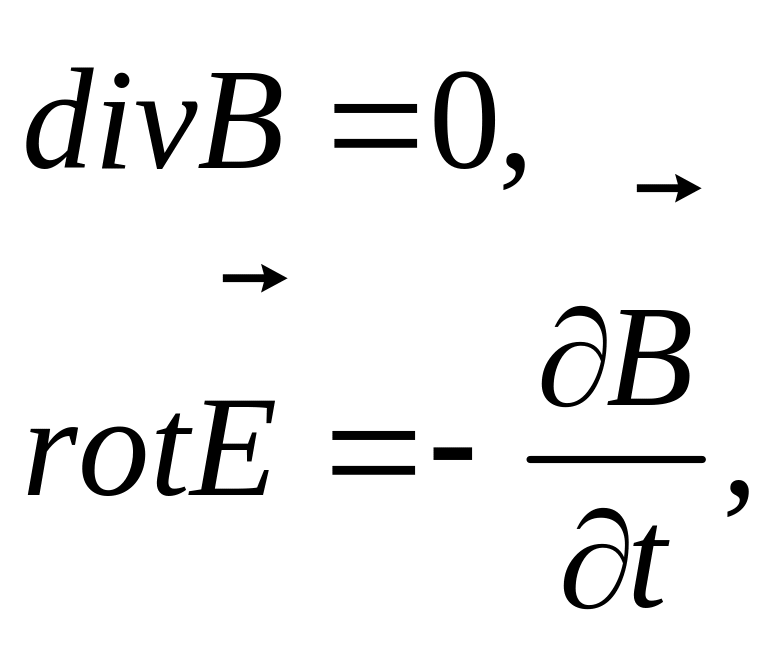(13.17)
які в компонентному записі представляються у вигляді чотирьох рівнянь:
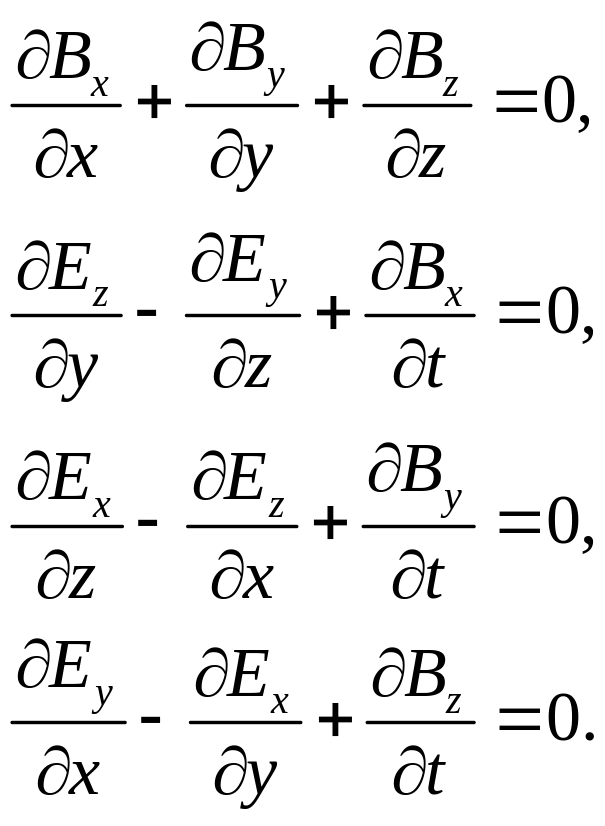
За допомогою дуального тензора електромагнітного поля (13.11) ці рівняння записуються так:
Додаючи до лівих частин
кожного рівняння нульові
доданки відповідно
і, одержимо
(за аналогією з
одержанням рівняння (13.15)) остаточний
запис пари рівнянь Максвела (13.17) у
чотиривимірній формі:
,
(13.18)
Таким чином, ми довели, що рівняння Максвела (5.1) (5.4) можна записати у вигляді двох чотиривимірних векторних рівнянь (13.15) і (13.18) у П-Ч Минковского, що і доводить релятивістську інваріантість рівнянь Максвела для зарядів і струмів у вакуумі. Відзначимо тут, що рівняння Максвела для електромагнітних явищ у матеріальних середовищах не мають релятивістської інваріантності (так як містять такі електричні і магнітні параметри середовища, що залежать від вибору ІСВ).
Зауваження. Ми записали пару рівнянь Максвела (13.17) у чотиривимірній формі (13.18), істотно використовуючи поняття дуального тензора електромагнітного поля. У зв'язку з цим відзначимо, що за допомогою тензора F чи (F) це зробити неможливо, у чому легко переконатися безпосередньою перевіркою.