§12 Релятивістська інваріантна форма рівнянь для електромагнітних потенціалів.

У §6 ми довели, що при виборі калібрування Лоренца (6.4^/):

(12.1)

рівняння (6.9^//)  (6.10^//) для електромагнітних потенціалів і мають вигляд: (12.2)

(12.3)

де

(12.4)

є оператор Даламбера. Запишемо рівняння (12.1)  (12.3) у 4-мірній формі. Використовуючи чотиривимірні позначення, запишемо оператор Даламбера (12.4) у наступному вигляді (див. §10): 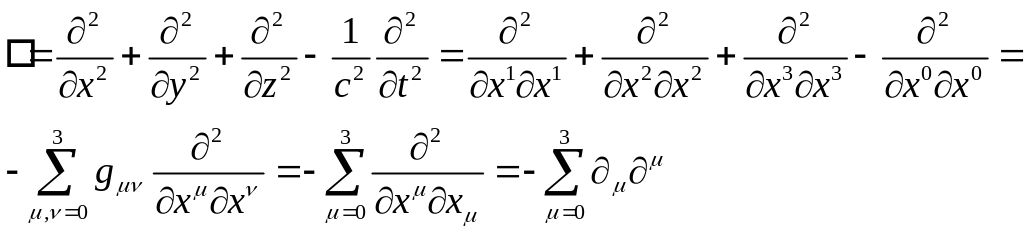(12.5)

,

звідки видно, що оператор Даламбера є чотиривимірний скалярний диференціальний оператор, що, відповідно до визначення чотирьохскалярів (10,…),є інваріантним перетворенням Лоренца, тобто має однаковий вигляд у всіх ІСВ ( ) і, отже, не змінює трансформаційних властивостей тих функцій, на які він діє (тобто після дії цього оператора скаляр залишається скаляром, вектор – вектором, тензор – тензором).

Далі, переписавши рівняння (12.2) у вигляді:

ми бачимо, що рівняння (12.2) – (12.3) можна об'єднати і записати в чотиривимірнім вигляді:

(12.6)

чи , ,

якщо ввести в розгляд (поки чисто формально) два чотирьохвектора: чотирьохвектор потенціалу електромагнітного поля (4-потенціал):

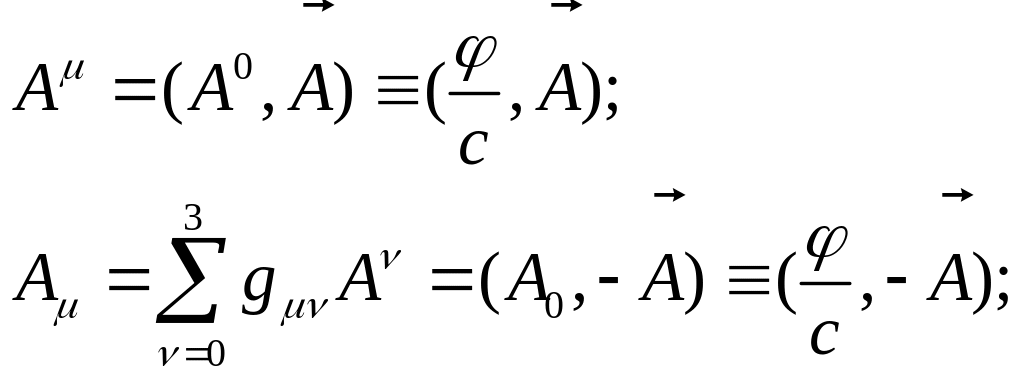(12.7)

і чотирьохвектор густини струму:

. (12.8)

Далі, калібрована умова Лоренца (12.1):

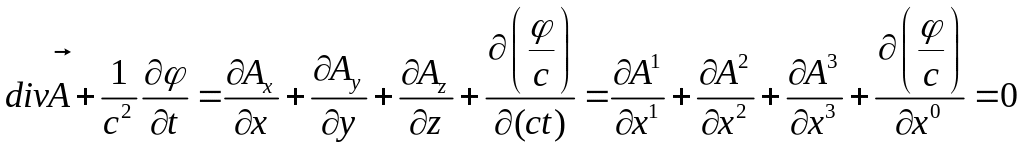
за допомогою 4-потенціалу (12.7) також можна записати в чотиривимірній формі:

(12.9)

ліворуч у (12.9) стоїть чотиривимірна дивергенція від А^, тому ліва частина (12.9) є чотирьохскаляром (якщо А^ - чотирьохвектор) і, отже, умова Лоренца (12.9) інваріантна щодо перетворень Лоренца.

Переконаємося тепер, що чотири величини ,визначені формулою (12.8), дійсно є чотирьохвектором. Нехай у системі k (див. §8) покоїться заряд ; у цій системі компонента згідно (12.8) має вигляд: (так як )

(12.10)

У системі , що рухається зі швидкістю v у позитивному напрямку осі ОХ, заряд рухається зі швидкістю , тому згідно визначення (12.8) маємо:

(12.11)

де  щільність заряду в системі . З іншого боку, припускаючи, що  4-вектор, ми повинні врахувати, що і зв'язано формулою (10, …), для чотирьохвекторов, тобто співвідношенням:

(12.12)

З (12.12) для компонентів одержуємо (з огляду на явний вигляд матриці Лоренца (10, …) і (12.10)):

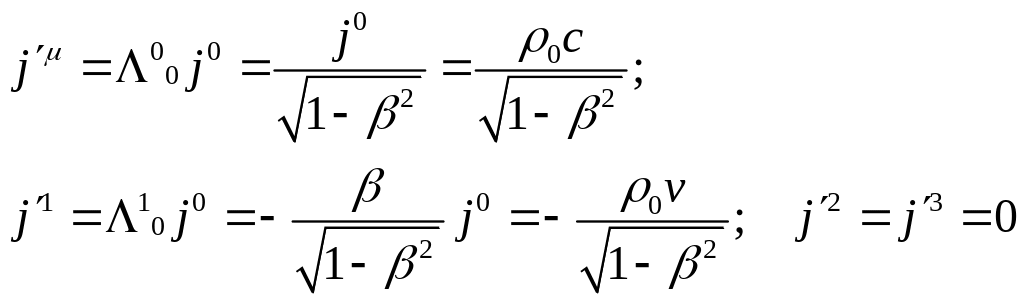
тобто, остаточно,

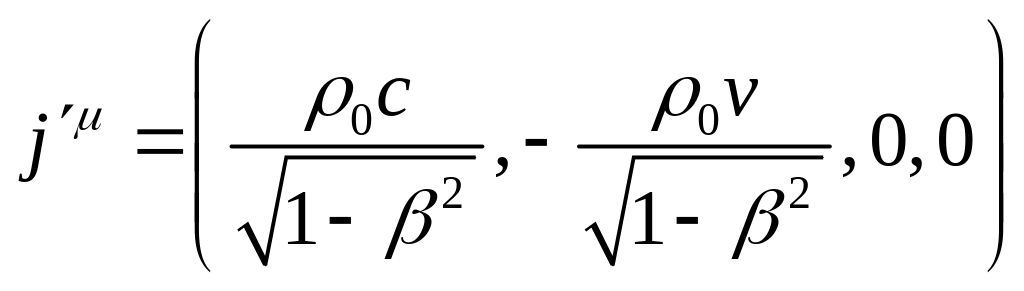(12.13)

Якщо  дійсно чотирьохвектор, то результати (12.11) і (12.13) повинні збігатися, а для цього необхідно, щоб густина зарядів у двох різних ІСВ були зв'язані між собою співвідношенням:

(12.14)

Таким чином, тільки при справедливості фізичного співвідношення (12.14) густина струму , визначена формулою (12.8), дійсно є чотирьох вектором. Але співвідношення (12.14) дійсно справедливо. Покажемо це, ґрунтуючись на наступному емпірично перевіреному факті: величина заряду у визначеному об'ємі не залежить від вибору системи відліку (наприклад, заряд протона однаковий у всіх ІСВ), тобто , чи

(12.15)

При перетвореннях Лоренца, унаслідок скорочення масштабів тіл у напрямку їхнього руху, маємо , тому з (12.15) випливає правило перетворення (12.14) для густини заряду: густина заряду, що рухається, більше густини заряду що покоїться ( > ₀).

Отже, є чотирьохвектор. Отже, права частина чотиривимірного рівняння (12.6) перетвориться як 4-вектор. Тому і ліва частина (12.6) повинна (у силу вимоги релятивістської інваріантості фізичних законів) перетворюватися як 4-вектор. З огляду на те, що оператор не змінює трансформаційних властивостей величини А^, ми дійдемо висновку, що і чотиривимірний потенціал А^ також є чотирьохвектором. Таким чином, представивши рівняння для електромагнітних потенціалів і умову Лоренца в чотиривимірній формі (12.6) і (12.9), ми довели їхню релятивістську інваріантість.

Зауваження. Легко бачити, що рівняння безперервності (7.1) також легко записується в чотиривимірній формі:

(12.16)