Iі Завдання додому
Розв’язати систему за допомогою методу Жордана-Гаусса:.
1)
2)
3)
Відповіді:
1)
= 1,
=
2,
=
3,
=
4
2) нескінченна множина розв’язків
3) система несумісна
Практичне заняття № 8
Тема: Вектори та дії над ними
Мета: сформувати вміння та навики виконання дій над векторами
Хід заняття
Вектором
називають напрямлений відрізок
з початком у точці
та кінцем у точці
.
Наприклад, у трьохвимірному просторі
точки
та
мають координати
та
відповідно, тоді вектор
має координати
.
Властивості та дії з векторами:
;
-
координати векторів
,
,
;
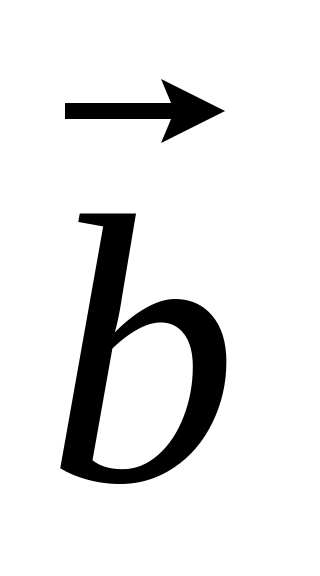;довжина вектора -
визначає також відстань між двома
точками
та
-
Скалярний
добуток двох векторів
та
дорівнює:
де
- косинус кута між векторами, який можна
визначити за формулою:
,
де
.
Вектори
та
паралельні, тоді
Для перпендикулярних векторів та скалярний їх добуток дорівнює нулю, тобто
Напрямні
косинуси вектора
:
,
,
,
-
кути, які утворює вектор
з осями
відповідно.
І Розв’язування вправ
1) Чи будуть вектори колінеарні?
(0; -4;
3), 
(0; 8; -6)
2) Дано:
(4х-2; 3; 0),
(5;
1; 3),
Знайти: х
3) Дано:
А (3; 1-у; 0), В (1; 2; 4), С (5; -1; 2z),
Знайти: у, z
4)
при якому значенні у
,
якщо
(-4; у; 3)?
5) Дано:
Знайти: ^
6) Знайти
напрямні косинуси вектора
Iі Завдання додому
1) Знайти
довжину вектора
і його напрямні косинуси
2)
Знайти
вектор
якщо А (1; 3; 2), В (5; 8; -1)
3) Знайти
проекції вектора
на осі координат, якщо
А (0; 0; 1), В (3; 2; 1), С (4; 6; 5), D
(1; 6; 3)
4) Обчислити модуль вектора і знайти його напрямні косинуси
5) Дано:
М1
(1; 2; 3), М2
(3; -4; 6). Знайти довжину і напрям вектора
6)
Знайти скалярний добуток векторів
і
7) Дано:
Знайти m
8) Дано:
Знайти: ^
9) Дано: (3; у-1; 4) (12; 3; z)
і колінеарні
Знайти: у і z
10) Дано:
А (2х-1; 3; 4), В (1; 0; 4), С
(3; 7; 1), D
(2;
5; – 1),
Знайти: х
Відповіді:
1)
=
70; cos
=
,
cos
=
,
cos
= –
2) (4; 5; - 3)
3) (0; 2; - 2)
4)
=
;
cos
=
,
cos
=
cos
=
5)
= 7;
cos
=
,
cos
=
–
,
cos
=
6) 0
7) m = 4
8) arccos
9)
y =
,
z
= 16
10) х = – 2
Практичне заняття № 9
Тема: Розклад вектора за базисом
Мета: сформувати вміння та навики розкладання вектора за базисом
Хід заняття
Базисом
-вимірного
простору називається сукупність
лінійно незалежних векторів цього
простору, наприклад,
,
,…,
,
для яких виконується умова
тільки коли
,
де
- дійсні числа.
Будь-який
вектор
-вимірного
простору можна представити у вигляді
лінійної комбінації векторів базису:
І Розв’язування вправ
1) Довести
, що вектори
1
=(1; 0; 2; 1),
2
=(2; 1; -1; 0),
3
=(-1; 2; 0; 0),
4 =(3; 0; 0; 0) лінійно незалежні.
2) Чи утворюють вектори 1 (3; -2; 1), 2 (-1; 1; -2), 3 (2; 1; -3) базис і якщо утворюють, то розкласти вектор (11; -6; 5) за цим базисом.
3) Самостійно: Розкласти вектор =(12; 9; 10) за базисом 1 (5; 4; 3),
2=(-3; -1; 2), та 3=(-3; 1 ; 3)
4)
Обчислити скалярний добуток векторів:
=(2;
0; -1; 3; 5),
=(1;
2; 3; 4; 5).
5)
Обчислити норму вектора: 
6) Дано: =(1; -2; 4), =(3; 0; -1)
Знайти:
напрямні косинуси вектора
7) Дано: А (-1; 3; -7), В (2; -1; 5), С (0; 1; -5)
Знайти:
(самостійно)
^
8) Дано:
, 
, 
Знайти:
(самостійно)