3.3. Основные показатели надежности программного обеспечения

Если рассматривать отказавшее ПО без учета его восстановления, а также случайный характер отказов в программах, то основные показатели надежности в этом случае не отличаются от тех, которые были рассмотре- ны в п.п. 2.2. – 2.4. При этом характер изменения этих показателей во вре- мени будет зависеть от модели надежности ПО.

Таким образом, основными показателями надежности ПО являются:

-вероятность безотказной работы программы p(t), представляющая со-

бой вероятность того, что ошибки программы не проявятся в интервале времени (0, t);

-вероятность отказа программы q(t) или вероятность события отказа ПО до момента времени t ;

-интенсивность отказов программы λ(t);

-средняя наработка программы на отказ T , являющаяся математическим ожиданием временного интервала между последовательными отказами.

При определении характеристик надежности ПО учитывается тот факт, что возникающие при работе программ ошибки устраняются, коли- чество ошибок уменьшается и, следовательно, их интенсивность понижа- ется, а наработка на отказ программы увеличивается. В связи с такими предположениями рассматривается несколько моделей надежности ПО: модель с дискретно-понижающей частотой появления ошибок, модель с дискретным увеличением наработки на отказ или ошибку ПО, экспоненци- альная модель надежности ПО.

3.3.1. Модель с дискретно-понижающей частотой появления ошибок ПО

Вэтой модели предполагается, что интенсивность отказов программы

λ(t) является постоянной величиной до обнаружения возникшей ошибки

42

и, как следствие – отказа программы и ее устранения. После этого значе-

ние λ(t) уменьшается и интенсивность отказов снова становится констан-

той. В этой модели предполагается, что между λ(t) и числом оставшихся

в программе ошибок существует зависимость

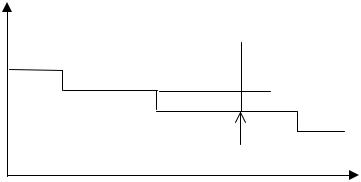
Характер изменения интенсивности отказов для этой модели представлен на рисунке 4.

λ(t)

K

t

Рис. 4. Характер изменения интенсивности отказов программы от времени наработки при модели с дискретно-понижающей частотой

появления ошибок

Плотность распределения времени обнаружения i -й ошибки ti опре-

деляется соотношением

f (ti ) = λie−λit i .

Значения неизвестных параметров K и M могут быть оценены на

основании последовательности наблюдения интервалов между моментами обнаружения ошибок.

На практике условия рассмотренной модели нередко не соблюдаются, а именно:

43

-не всегда при устранении ошибки интенсивность отказов уменьшается на одну и ту же величину K , так как разные ошибки имеют различное влияние на ход исполнения программы;

-довольно часто возникают ситуации, при которых устранение одних ошибок приводит к появлению новых;

-не всегда удается устранить причину ошибки и программу продолжают использовать, так как при других исходных данных ошибка может себя и не проявить.

3.3.2. Модель с дискретным увеличением времени наработки на отказ

Основным допущением в этой модели является предположение о том, что отказы и ошибки программы в начале эксплуатации возникают часто. По мере отладки программы таких ошибок становится меньше, а время на-

работки на отказ после ликвидации очередного отказа увеличивается

(рис.5).

t

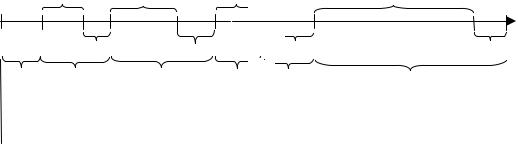
Рис. 5. Диаграмма интервалов времени наработки на отказ компьютерной программы

На диаграмме величины t1, t2, t3,K, tm−1, tm – случайные моменты

времени возникновения первого, второго, третьего и так далее – m-го от- казов. Величины t(1) , t(2) , t(3) ,K, t(m−1) , t(m) – случайные интервалы

44

времени между соседними отказами программы (обозначены под первым рядом нижних скобок диаграммы). Интервалы t(2) , t(3) , t(m−1) , t(m)

также являются случайными временными интервалами.

Пусть первая ошибка, проявившаяся в результате отказа программы,

произошла в случайный момент времени t1 и была устранена. Наработка до первого отказа и возникшей ошибки равна интервалу времени t(1) . Вто-

рая ошибка возникла в момент времени t2 . Наработка до второй ошибки определяется интервалом t(2) . В соответствии с предположением, этот ин-

тервал больше, чем t(1) , так как после перезапуска программа проработала время до первой ликвидированной ошибки, продолжила работу до новой,

второй ошибки. Следовательно, интервал t(2) можно представить в виде

t(2) = t(1) + t(2) ,

где t(2) – дополнение интервала t(1) до величины интервала t(2) .

Обобщая эти рассуждения до любого i -го интервала (i =1,m), можно

записать

t(i) = t(i−1) + t(i) .

Случайные величины t(i) являются независимыми, имеют математиче-

ское ожидание M[ t] и дисперсию σ 2t .

Случайное время возникновения (i − 1) ошибки ti отсчитывается от начального момента времени t0 = 0. Время, необходимое на ликвидацию ошибки, в расчет не берется. В этом случае для всех случайных моментов времени возникновения ошибки и временных интервалов между соседни- ми ошибками можно записать:

45

Учитывая, что от момента времени t0 = 0 до начала момента t1 не выяв-

лено ни одной ошибки программы и в силу того, что интервал t(1) сравни- тельно невелик, так как ошибки программы вначале ее эксплуатации про-

Рассмотрим выражение для t(i) при i =1. Согласно ранее принятой замене t(1) на t(1) , получим

t(1) = t(0) + t(1) = t(1) .

Действительно, интервал t(0) равен нулю, так как до начала эксплуатации программы никаких ее отказов произойти не могло. Поэтому для любого i = m при i >1 можно записать

m

t(m) = å t(i) . i=1

46

Но t(m) – это наработка между (m −1) и m – отказами. Тогда, для любых m, средняя наработка между (m −1) и m отказами равна математическо-

му ожиданию интервала t(m) :

m

tср(m) = M[t(m) ] = M[å t(i) ]. i=1

Но для любого i

M[ t(i) ] = M[ t].

Поэтому

m

tср(m) = M[å t(i) ] = i=1

Отсюда видно, что с увеличением между двумя отказами.

Рассмотрим среднюю наработку до возникновения m -го отказа. Она равна математическому ожиданию от tm :

Как и предыдущем случае, из полученного выражения видно, что средняя

наработка до отказа возрастает с увеличением числа отказов

Оценки M[ t] и σ 2t получаются по данным об отказах программы в

течение периода наблюдения tн :

где mн – число отказов за интервал времени (0, tн ).

47