p(nф ≤ n) и mn , можно найти величину количества устройств выбороч-

ной совокупности

Nв = mn . mλ t

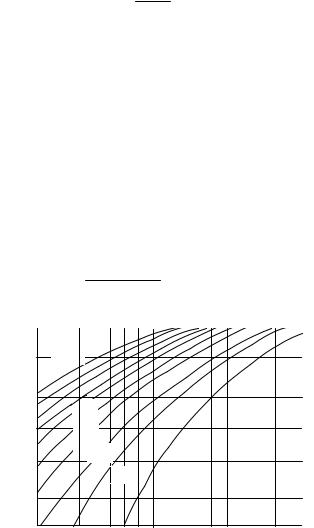
Пример 5.1. Необходимо провести испытание на надежность новых генераторов посто- янного тока. Согласно условиям, испытание производится в течение 100 часов. Пред- полагается, что в течение этого времени произошло более трех отказов с досто- верностью p(nф ³ n)=0,95.Ориентировочное значение математического ожидания ин- тенсивности отказов выбираем из справочных таблиц для аналогичных генераторов по-

стоянного тока λ =3 10 −4 . Математическое ожидание количества отказов находим по

графику рис. 23 nm = 6 . Размер выборки генераторов для испытания определяем по

формуле

0,0001 0,005 0,05 0,1 0,2 0,3 0,9 0,95 0,999 ln p(nф ³n)

Рис.23. Вспомогательный график для определения размера выборки

при испытании на надежность

8.3. Ускоренные испытания на надежность

Ускоренные испытания ТУ на надежность проводятся в рабочем ре-

жиме с повышенными нагрузками и представляют собой разновидность метода физического моделирования.

126

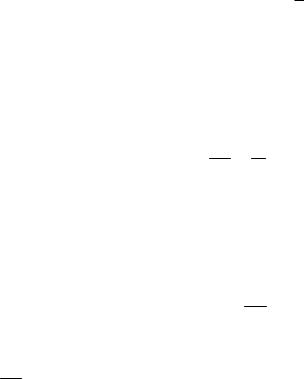
Для экспоненциального закона вероятность безотказной работы равна

− t

p(t) = e T .

Если безразмерные коэффициенты модели и реального процесса рав- ны, то в этом случае метод физического моделирования для опыта приме- ним. В данном случае

tу = t =τ ,

Tу T

где tу и Tу – временные характеристики надежности при ускоренных

испытаниях. Отсюда

t = T tу , Tу

где T = k – коэффициент подобия.

Tу

Аналогично можно написать

p(t) = p(tу ).

Коэффициент подобия выражает собой величину соответствия време- ни работы ТУ в условиях нормальной эксплуатации одному часу ускорен- ных испытаний.

Для любых элементов ТУ вероятность безотказной работы является функцией комплексной нагрузки Z и времени работы t :

p =ψ (Z,t).

Комплексная нагрузка включает в себя различные частные нагрузки, влияющие на величину интенсивности отказов, например, для информационных систем:

Z = ϕ (U,Q,t0,V ,K),

127

где U – качество электропитания информационной системы;

Q и t0 – влажность и температура окружающей среды соответственно;

V – объем перерабатываемой информации и другие нагрузки.

Комплексная нагрузка может быть выражена в виде безразмерного коэффициента ξ . Тогда выражение для вероятности безотказной работы

можно записать в виде

p=ψ1(ξ,t)

ианалогично для ускоренных испытаний:

pу =ψ1(ξу ,tу ) ,

где ξ = ξ у , t = tу , p = pу .

Эти равенства и служат критерием соответствия параметров при ус- коренных испытаниях и в реальных условиях эксплуатации.

Чем больше коэффициент подобия, тем больше сокращается срок проведения испытаний, однако надо учитывать, что при достаточно боль-

ших значениях коэффициента подобия может быть нарушено соответствие между вероятностями p и pу .

Для экспоненциального закона распределения оценка среднего време-

ни безотказной работы при ускоренных испытаниях равно

Tу = Nt1у ,

где t1у – время появления первого отказа при ускоренных испытаниях;

N – количество однотипных ТУ или элементов, поставленных на ус- коренные испытания. Очевидно, что чем больше число N , тем достовер-

нее станет величина Tу .

128

Из выражения коэффициента подобия k и среднего времени безот-

казной работы при ускоренных испытаниях Tу определяется среднее вре-

мя безотказной работы для реальных условий:

T = kTу = kNt1у .

Если определить некоторое заданное время работы испытуемого ТУ как tз и минимальное допустимое время безотказной работы Tmin для это-

го случая, то время ускоренных испытаний может быть определено из со-

отношения

tу = tkз = TNmink .

Количество ТУ, необходимое для проведения ускоренных испытаний на надежность с учетом желаемой точности эксперимента, может быть оценено на основании следующего выражения:

N = lg[1− Q(tу )] , lg p(ty )

так как статистическая вероятность отказа, полученная при ускоренных испытаниях N ТУ, определяется по формуле

Q *(tу ) =1−[ p *(tу )]N ,

где p *(tу ) – статистическая вероятность безотказной работы одного испытываемого ТУ.

8.4. Метод статистического моделирования надежности

Метод статистического моделирования надежности основан на так на- зываемом методе Монте-Карло. Суть метода Монте-Карло состоит в ис-

пользовании данных предыдущего опыта для оценки возможных ситуаций в будущем. Принципиальная особенность метода состоит в том, что влия- ние различных случайных факторов в процессе опыта учитывается не рас-

129

четным, а игровым способом. В качестве универсального механизма слу- чайного выбора используется совокупность случайных чисел, равномерно распределенных в интервале (0 – 1), которые вырабатываются датчиком случайных чисел. Случайные числа используются для получения дискрет- ного ряда случайных переменных, имитирующих результаты, которые можно было бы ожидать в соответствии с вероятностным распределением, полученным на основании предыдущего опыта.

Метод Монте-Карло можно проиллюстрировать на довольно простом примере. Пусть под наблюдением находится некоторое количество про- стых ТУ. Каждые 100 часов число отказов этих устройств соответствует распределению, приведенному в таблице 4.

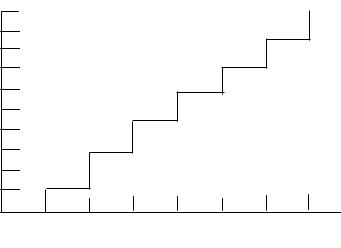
По этой таблице строим график распределения кумулятивной вероят- ности (график закона распределения) случайной величины – число отказов ТУ (рис. 24).

Пусть в дальнейшем необходимо получить предполагаемое число от- казов для шести аналогичных периодов времени. Для этого запускается

ранее описанный датчик случайных чисел и фиксируются шесть первых полученных значений. Пусть это будут значения: 0,1; 0,22; 0,37; 0,17; 0,56; 0,87. Полученные случайные числа можно рассматривать как вероятности.

130

деления числа отказов, полученных на основании ранее проведенных на- блюдений).

Если мы располагаем совокупностью распределенных случайных ве-

личин yi (i = 1, 2, K, n) в интервале (0 – 1), то каждой из них соответст-

вует определенное для данного вида функции F(x) = y число x i , значе-

ние которого находится обратным преобразованием (то есть то значение аргумента x , для которого F(x) = yi ).

Отсюда следует, что процесс получения последовательности случай-

ных чисел x i с заданным законом распределения F(x) сводится к реше-

нию относительно x i уравнения

∞

F(x) = ò f (x) dx = y .

−∞

Например, если требуется реализовать случайную величину t , рас- пределенную по экспоненциальному закону с известным значением λ :

F (x) = 1− e−λ t ,

то на основании ранее приведенных соображений получим

1− e−λ t = q .

Тогда, очевидно,

t i = − λ1 ln(1− qi ),

где qi – последовательность случайных чисел, распределенных в интерва-

ле (0 – 1), вырабатываемых датчиком случайных чисел.

Результаты моделирования представляют собой статистические сред- ние значения величин, фиксируемые в качестве искомых параметров:

132

m* 1 N x ,

x = N iå=1 i

где xi – численное значение искомого параметра в i -ой реализации;

N– число реализаций алгоритма.

Всоответствии с известными предельными теоремами теории вероят- ностей среднее значение стремится к действительному ожиданию случай- ной величины при неограниченном возрастании числа испытаний.

На практике число испытаний ограничено. В силу этого значение ис- комого параметра в известной степени будет случайным, то есть вместо точного будет получено его приближенное значение, или оценка, имеющее лишь ограниченную точность. Абсолютная величина максимального от- клонения определяется следующим образом:

ε= tασ m ,

где tα = 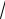2Ф−1(α) представляет собой количество величин среднеквад-

ратических отклонений σ m для нормального закона распределения, кото-

рую нужно отложить вправо и влево от центра рассеивания, чтобы вероят-

ность попадания на полученный интервал была равна α . Значения tα та-

булированы, Ф−1(α ) – функция, обратная функции Лапласа. Это означает,

что каждому значению аргумента α соответствует определенная величина функции Лапласа, равная tα .

Применение современных ЭВМ позволяет осуществить исследование самых разнообразных систем и при этом имитировать реальные условия эксплуатации. В этом случае большое значение имеет разработка стан- дартных программ и алгоритмов для решения типовых задач надежности. Основой для разработки программ может быть методика, приведенная ни- же.

133

Основной характеристикой, необходимой для проведения расчетов,

является вероятность пребывания системы в определенном состоянии

Pi (t) для заданного интервала времени τ , при котором она способна нор-

мально функционировать. В сложных ТУ таких состояний может быть большое количество. Для определения конкретных состояний на учет бе- рутся все элементы устройства, каждый из которых может находиться в одном из двух состояний: исправном или неисправном.

В результате предварительного анализа процесса функционирования устанавливается число рассматриваемых состояний, при которых ТУ спо- собно функционировать, при этом маловероятные ситуации обычно ис- ключаются.

Методика решение задачи оценки надежности методом статистиче- ского моделирования системы сводится к следующему: заданный интервал времени τ разбивается на равные промежутки

t = τk

и для каждого t определяется состояние каждого элемента системы в со-

ответствии с принятыми законами распределения времени безотказной ра- боты. Эта информация используется для определения рабочих состояний ТУ, соответствующих некоторому рассматриваемому промежутку времени t . Все состояния системы нумеруются в порядке убывания показателей надежности. Затем фиксируется состояние с наименьшим номером, то есть

выбирается состояние системы с наилучшей по надежности комбинацией исправных элементов.

Аналогично этот процесс повторяется для следующего промежутка времени и так далее. Многократное повторение этого процесса для каждо- го t позволяет получить оценку для вероятности исправного j -го со-

стояния p j (t) в момент времени t , принадлежащему τ .

134