Глава 2 Основные показатели надежности невосстанавливаемых

технических устройств

2.1.Составляющие надежности

Всоответствии с определением, надежность является сложным свой- ством. Именно благодаря надежности, ТУ выполняет определенные функ- ции, делая это в течение некоторого срока, с заданным качеством. Это происходит вследствие наличия таких составляющих надежности, как без-

отказность, ремонтопригодность, долговечность и сохраняемость. Безотказность – это способность ТУ работать без отказа в тече-

ние некоторого времени.

Долговечность – свойство ТУ сохранять работоспособность с необ- ходимыми перерывами для технического обслуживания и ремонта до пре- дельного состояния, оговоренного в технической документации.

Сохраняемость – это свойство ТУ сохранять работоспособность при хранении до начала эксплуатации, в перерывах между периодами экс- плуатации и после транспортировки.

Ремонтопригодность – свойство конструктивной приспособленно- сти ТУ к выявлению, устранению и предупреждению в них неисправно- стей.

Эта составляющая разделяет все ТУ на восстанавливаемые (ремон- тируемые) и невосстанавливаемые (неремонтируемые). К последним отно- сятся такие ТУ, ремонт которых в случае отказа не предусмотрен и не про- изводится. Они составляют достаточно большую часть технических уст- ройств, так как в большинстве случаев являются элементами сложных тех- нических систем.

20

Названные свойства относятся так называемым единичным показа- телям надежности, объединенным в комплексное понятие собственно на- дежности.

Рассмотрим эти и другие показатели, характеризующие надежную работу ТУ, относящимся к неремонтируемым, так как эти показатели носят ключевой характер в теории надежности.

2.2. Простейший поток отказов

ТУ – это наиболее общее название технических объектов. Они могут быть сложными и простыми. В теории надежности различают понятие сис-

тема и элемент.

Элемент - составная часть сложного ТУ, которая при расчете и ис- следовании надежности не подлежит расчленению. Система – совокупно- сти совместно действующих элементов, предназначенная для выполнения определенных заданных функций.

Тогда отказ системы может наступить при отказе одного элемента этой системы.

В теории надежности, наряду с другими, рассматривают простейший поток отказов, который соответствует простейшему потоку случайных со- бытий. Простейший поток обладает следующими свойствами:

-стационарность,

-ординарность,

-отсутствие последовательности.

Стационарность определяется тем, что вероятность появления то- го или иного числа отказов на некотором временном интервале эксплуа- тации t зависит только от длины этого интервала, но не зависит от по- ложения этого интервала на оси времени.

Иными словами, предполагается, что отказы распределены на оси времени в процессе эксплуатации с одинаковой средней плотностью λ .

21

Ординарность определяется тем, что вероятность возникновения двух или более отказов системы в некоторый момент времени t пренеб- режимо мала по сравнению с вероятностью одного отказа.

Это означает, практически, что одновременно в системе отказа более двух элементов быть не может.

Отсутствие последствия определяется тем, что наступление отка- за в момент ti не зависит от того, сколько отказов и в какие моменты времени они возникали до момента ti .

Поскольку простейший поток отказов соответствует простейшему по- току событий, то он подчиняется закону Пуассона. Закон Пуассона гласит:

Если случайная величина ξ в простейшем потоке событий за время

τ некоторое целое положительное значение K , то эта величина распре- делена по закону Пуассона:

p(ξ =K)= aK e− a. K!

Статистический смысл параметра a заключается в том, что a – это среднее число событий, наступающих в простейшем потоке за время τ :

a =λτ .

С точки зрения надежности случайная величина ξ представляет со-

бой число отказов ТУ, а число p(ξ =K) представляет собой вероятность появления ровно K отказов ТУ за время τ . Представляет интерес вероят-

ность отсутствия отказов или вероятность работы ТУ без отказов в течение времени τ :

p(ξ =0) = a0 e− a = e−a = e−λτ .

0!

Тогда вероятность противоположного события, заключающегося в том, что за время τ произойдет хотя бы один отказ, будет равна

22

p(ξ ³1) = 1- p(ξ = 0) =1- e−λτ .

Особенность закона Пуассона заключается в том, что математическое ожидание и дисперсия равны между собой и равны величине a :

Mξ = Dξ =a.

2.3. Вероятность безотказной работы и вероятность отказов

Надежность как качественная характеристика всегда принималась во внимание при решении различных вопросов эксплуатации и технического обслуживания. Количественное определение надежности появилось с воз- никновением теории надежности. Математической платформой теории на- дежности являются теория вероятностей и математическая статистика. Действительно, отказы в ТУ происходят случайным образом в неожидан- ные моменты времени. Это характерно даже для множества однотипных устройств, изготовленных на одном предприятии и поставленных на экс- плуатацию в одно и то же время. Несмотря на единый проект, одинако- вость технологии производства – каждый из них имеет индивидуальную способность сохранять свои первоначальные качества. Первоначально ка- жется что никакой закономерности в появлении отказов нет. Тем не менее, такая закономерность существует. Проявляется она тогда, когда ведется наблюдение не за одним, а за многими ТУ, находящимися в эксплуатации.

В качестве основной количественной меры надежности ТУ, характе- ризующей закономерность появления отказов во времени, принята веро-

ятность безотказной работы.

Вероятность безотказной работы (ВБР) – это вероятность того, что за определенное время работы ТУ и в заданных условиях эксплуата- ции отказа не происходит.

Поскольку возникновение отказа является случайным событием, то и время его возникновения to – также событие случайное. Поэтому ВБР:

23

p(t) = p(to ³ t),

где t – заданное время работы.

Вероятность появления отказа – это вероятность противополож- ного события:

q(t) = p(to < t).

Но событие отказа и событие безотказности – суть противоположные события. Поэтому, в соответствии со свойством вероятностей противопо- ложных событий, можно записать

p(t) + q(t) = 1.

На практике определяют оценки этих вероятностей. Пусть N – это общее количество однотипных ТУ, эксплуатируемых в течение времени t .

За это время N (t) ТУ работало безотказно, а n(t) – отказало. Таким обра-

зом:

N = N(t) + n(t) ,

то есть через время t общее количество как исправных, так и отказавших ТУ равно первоначальному. Статистическая вероятность безотказной ра-

боты определяется выражением

p* (t) = NN(t) ,

а частота отказов

q* (t) = nN(t) .

Найдем сумму этих частот:

что соответствует теоретическим выводам.

24

Для перехода от p* (t) и q* (t) к p(t) и q(t) нужно взять предел от-

ношений частот:

p(t) = lim N(t) ,

N →∞ N

q(t) = lim n(t) .

N→∞ N

Так как N → ∞ достичь невозможно, то под этой декларацией на

практике можно подразумевать весь парк поставленных на эксплуатацию однотипных ТУ.

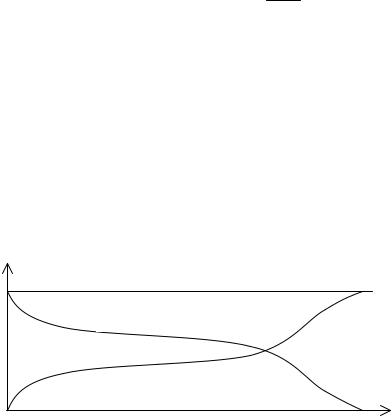
Очевидно, что с течением времени общее количество отказов в ТУ увеличивается. Следовательно, увеличиваются и q(t), а, значит, уменьша-

ется p(t). Кривые, определяющие характер этих изменений, имеют вид:

p(t), q(t)

1

p(t)

q(t)

Рис. 1. Характер изменения кривых p(t) и q(t)

На практике часто необходимо определить надежность ТУ в течение некоторого интервала времени от ta до tb (например, в течение периода работы этого устройства) при условии, что оно уже находилось в эксплуа-

тации некоторое время tb . ВБР ТУ за время (tb − ta ) при условии, что оно безотказно проработало в течение ta часов, определяется условной веро-

ятностью

25

p(tb t−a ta ) = p(to ³ tb ).

Эта условная вероятность численно равна вероятности p(tb ). Дейст-

ta

вительно, вероятность того, что объект не отказал в течение времени

(tb − ta ) при условии того, что он безотказно проработал ta часов, скла-

дывается из ВБР в течение ta часов и ВБР в течение часов от ta до tb . Со-

гласно понятию условной вероятности,

Но p(tb ,ta ) численно равна вероятности того, что ТУ безотказно прора-

ботает tb часов:

p(tb ,ta ) = p(tb ).

Тогда

так как

Используя величину вероятности безотказной работы p(t), можно

оценить среднее количество элементов или устройств ИС (например, сети,

ЭВМ или ее периферии) n(t), которые могут отказать за интервал времени t при известной наработке t :

26