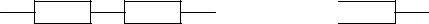
Глава 6 Структурные схемы надежности
Ранее говорилось о том, что ТУ подразделяются на элементы и систе- мы, причем система состоит из элементов. Элементы, составляющие сис- тему, могут быть соединены между собой различным образом. С точки зрения надежности, такие соединения представляют собой структуры, ка- ждая из которых имеет свой способ расчета. Такой расчет представляет собой расчет надежности. Сами структуры носят название структурных схем надежности. Структурные схемы надежности нельзя путать с прин- ципиальными, функциональными, структурными и другими схемами сис- тем, хотя в частных случаях они могут совпадать. Соединение элементов в структурных схемах надежности можно свести к четырем видам:
-последовательному,
-параллельному,
-смешанному,
-произвольному.
Вкачестве основных показателей надежности здесь используются ве- роятность безотказной работы и вероятность отказа.
6.1. Структурные схемы надежности с последовательным соединением элементов
Последовательное соединение в структурной схеме надежности – это такое соединение, при котором отказ хотя бы одного элемента при-
водит к отказу всей системы в целом (рис. 9). |
|
|
1 |
2 |
n |
. . . 
Рис. 9. Структурная схема надежности с последовательным соединением элементов
82
Этот тип соединения в теории надежности еще называет основным со-
единением.
Если считать отказы элементов независимыми, то на основании тео- ремы умножения вероятностей, вероятность безотказной работы ТУ выра- жается следующим образом:
n
Pc (t) = p1(t) × p2 (t) ×...× pn (t) = Õ pi (t),
i=1
где pi (t)– вероятность безотказной работы i -о элемента;
Pc (t) – вероятность безотказной работы системы.
Если
p1(t) = p2 (2) = ... = pn (t) = p(t) ,
то
Pc (t) = pn (t) .
С учетом выражения вероятности безотказной работы через интенсив-
ность отказов можно записать
|
t |
n t |
t n |
|
|
n −òλ i (t)dt |
−åòλi (t)dt |
−òåλ i (t)dt |
|
P (t) = П e 0 |
= e i=1 0 |
= e 0 i=1 |
. |
|
c |
i=1 |
|
|
|
|
|
|
|
|
Отсюда можно сделать заключение, что суммарная интенсивность от- казов n последовательно соединенных элементов находится как сумма ин- тенсивностей отдельных элементов.
n
λΣ (t) = åλi (t),
i=1
или, для случая равнонадежных элементов,
λΣ (t) = nλ(t).
Для случая λ = const имеем
83
n
−åλit
P (t) = e i=1 ,
c
откуда
n
λå = åλi .
i=1
Из последнего выражения видно, что для обеспечения требуемой тех-
ническими условиями вероятности безотказной работы ТУ при увеличении числа последовательно соединенных элементов необходимо снижать вели- чину интенсивности отказов каждого элемента или, что то же самое, при- нимать меры к увеличению их средней наработки на отказ.
Нередки случаи, когда система последовательно соединенных элемен-
тов состоит из k подсистем, а каждая j -я ( j =1,k) подсистема состоит из n j равнонадежных элементов. В этом случае вероятность безотказной
работы системы будет определяться выражением
k n (t)
Pc (t) = Õ p j ,
j =1
где n j – количество равнонадежных элементов j -о типа; p(t)– вероят-
ность безотказной работы элемента j -й подсистемы.
Суммарная интенсивность отказов равна
k
λΣ (t) = ån jλ(t) .
j =1
Анализ полученных выражений показывает:
-вероятность безотказной работы будет тем ниже, чем больше элементов в него входит;
-вероятность безотказной работы последовательного соединения будет ниже, чем эта же вероятность у самого надежного элемента системы.
84
6.2. Структурные схемы надежности с параллельным соединением элементов
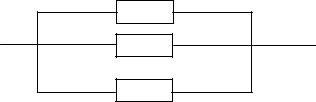
Параллельным соединением элементов в структурной схеме надеж- ности называется такое соединение, при котором система отказывает только при отказе всех n элементов, образующих эту схему (рис. 10).
Согласно определению,
n |
n |
- pi (t)). |
Qc (t) = q1(t) × q2 (t) ×...× qn (t) = ∏ qi (t) = ∏(1 |
||
i=1 |
i=1 |
|
Отсюда
n
Pc (t) =1- Qc (t) =1- ∏(1- pi (t)) .
i=1
1
2
n
Рис. 10. Структурная схема надежности с параллельным соединением элементов
С учетом интенсивности отказов выражение примет вид
|
|
t |
|
|
n |
òλ i (t)dt |
|
P (t) =1- П (1 |
- e0 |
). |
|
c |
i=1 |
|
|
|
|
|
|
Для случая равнонадежных элементов имеем |
|
||
|
|
t |
|
|
|
−òλ(t)dt |
)n , |
P (t) =1- (1- e o |
|||
c |
|
|
|
а при λ = const последнее выражение примет вид
n |
- e−λit ) . |
p (t) =1- ∏(1 |
|
c |
|
i=1 |
|
85