11.2. Различные формы уравнения бернулли. Скорость распространения малых возмущений в газе

Уравнение Бернулли (см. п. 5.7) для адиабатного течения идеального газа

широко используется в газовой динамике в нескольких формах. Одну из них получим, заменив в нем отношение р/ по уравнению состояния на RT:

(11.19)

Из этого выражения следует, что при увеличении скорости газового потока (его ускорении) температура уменьшается, а при

торможении увеличивается. Такой характер изменения температуры обусловлен теплоизолированностью процесса. Учитывая выражение энтальпии

представим уравнение (11.19) в форме

совпадающим с уравнением сохранения энергии (11.6).

Заметим, что если бы мы рассматривали теплоизолированное движение газа с трением, то и в этом случае уравнение (11.19) Бернулли оказалось бы справедливым. Действительно, хотя на преодоление сил трения была бы израсходована часть механической энергии, но она преобразовалась бы в теплоту, что привело бы к увеличению внутренней энергии U, поэтому сумма i + u²/2 осталась бы неизменной.

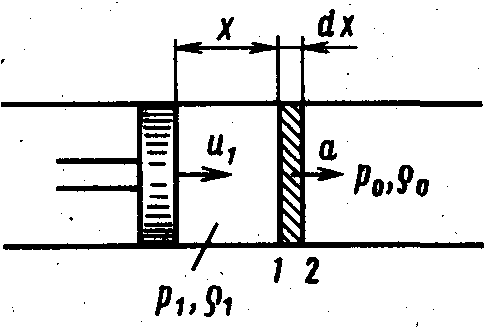
Для получения иных употребительных в газовой динамике форм уравнения Бернулли определим скорость распространения в газе малых механических возмущений. Для этого рассмотрим покоящийся газ, заполняющий цилиндрическую трубу с площадью S поперечного сечения справа от поршня (рис. 11.1). Параметры покоящегося газа обозначим р₀ и ₀. Если поршню сообщить внезапное малое перемещение со скоростью u₁, это приведет к уплотнению газа перед ним, повышению давления на р = p₁ — р₀ и плотности на  = ₁ — ₀. Возмущение распространится в газе с некоторой скоростью а и по истечении времени охватит область х, а за время dt распространится еще на расстояние dx = adt. Частицы газа в зоне уплотнения приобретут скорость u₁ поршня. Чтобы найти скорость а распространения возмущения, используем законы сохранения массы и изменения количества движения.

В момент t + t ( в объеме, ограниченном сечениями 1 и 2, масса составит Sdx = ₁Sadt. Эта масса должна равняться сумме первоначальной массы этого объема ₀Sdx = ₀Sadt и привнесенной в него массы ₁u₁dtS, т. е.

(11.20)

Уравнение изменения количества движения выделенного отсека жидкости имеет вид

откуда

(11.21)

Рис. 11.1. Схема дли определения скорости распространения малых возмущений

Исключая из уравнений (11.20) и (11.21) скорость u₁, получаем

Если изменение р давления и соответствующее изменение  плотности малы, то, переходя к бесконечно малым, можно записать

a² = dp/d или а == (11.22)

Из физики известно, что акустические (звуковые) волны представляют собой последовательные малые сжатия и разрежения упругой среды, поэтому полученная формула выражает скорость распространения звука в газе. Заметим, что все рассуждения, из которых она выведена, справедливы и для любой другой упругой среды. Поэтому формула (11.22) выражает скорость звука в таких средах. В частности, если среда при малых сжатиях подчиняется закону Гука (см. гл. 1)

то формула (11.22) для нее примет вид

В частности, это выражение пригодно для капельных жидкостей. При распространении малых возмущений в газе сжатие или разрежение происходят настолько быстро, что теплообмен между частицами не успевает осуществляться и процесс протекает адиабатически, т. е. связь между плотностью и давлением выражается уравнением адиабаты

Д ифференцируя это уравнение, получаем

или

Следовательно, для газов скорость звука или скорость распространения малых возмущений

(11.23)

Из формулы (11.23) можно сделать вывод, что скорость звука в газе зависит только от его молекулярной структуры и температуры и не зависит от условий движения.

Теперь запишем уравнение Бернулли (11.19) в форме

(11.24)

из которой следует, что при возрастании скорости адиабатного течения газа скорость звука в нем уменьшается, а при убывании — увеличивается. Разумеется, эта зависимость скорости звука от скорости газа есть лишь результат изменения температуры газа при изменении скорости течения. Следует также подчеркнуть,

что в левой части уравнения (11.24) скорость звука а относится к той же точке (или сечению) газового потока, где имеет место скорость и течения, т. е. она представляет собой местную ско­рость звука.