3. Растяжение и сжатие

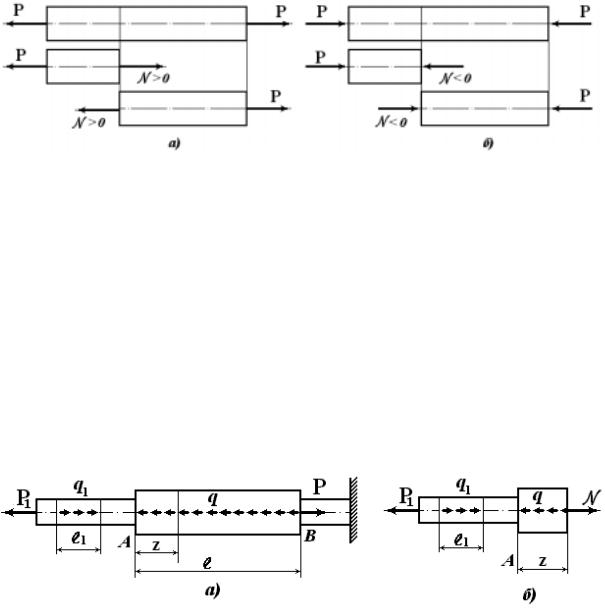
Растяжение или сжатие бруса вызывается действием внешних сил вдоль оси бруса. При растяжении в поперечных сечениях бруса (стержня) возникают только нормальные силы N. В предыдущем разделе были рассмотрены простейшие схемы растяжения (рис. 3.1,а) и сжатия (рис. 3.1,б) при испытании образцов.

Рис. 3.1

Принято, что при растяжении нормальная сила положительная (N>0) и направлена от сечения, а при сжатии нормальная сила отрицательная (N<0) и направлена к сечению. В рассматриваемых простых случаях при растяжении N = P (см. рис 3.1,а) и при сжатии N = - P (см. рис. 3.1,б). Рассмотрим определение нормальных сил в более сложных случаях.

3.1. Определение нормальных сил

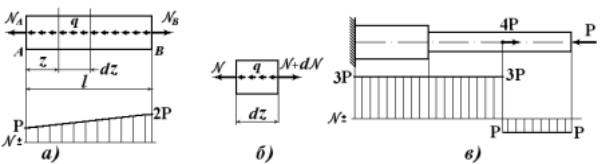
Нормальная сила N в произвольном сечении стержня определяется по методу сечений. Рассмотрим нагружение стержня сосредоточенными силами и равномерной погонной нагрузкой qi = const (рис. 3.2,а).

Рис. 3.2

В произвольном сечении бруса на участке АB нормальная сила N определяется из условия равновесия отсеченной части (рис. 3.2,б). В данном случае отброшена правая часть стержня, так как в заделке предварительно реакция не определена. Нормальная сила направлена

35

от сечения, т.е. в положительном направлении. Уравнение равновесия имеет вид:

Σ Fz = 0 , -P1 + q1l1 – qz + N = 0 → N = P1 – ql1 + qz.

Выражение для N можно записать сразу, если придерживаться следующего правила: нормальная сила в сечении равна алгебраической сумме всех сил, действующих на оставшуюся часть стержня:

где Pi - сосредоточенные силы и равнодействующие распределенных нагрузок.

При этом внешняя сила условно считается положительной, если растягивает рассматриваемый участок, и отрицательной, если сжимает. Например, в выражении (3.1) сила Р1 и равнодействующая сила qz растягивают участок длиной z, а равнодействующая сила q1l сжимает

(см. рис. 3.2,б).

При z = 0 нормальная сила в сечении А равна: NA = P1- q1l1. При z = l нормальная сила в сечении В равна: NВ = P1- q1l1+ql.

Значения NА и NВ можно получить непосредственно в сечениях, расположенных справа и слева от границ участка АВ (см. рис. 3.2,а).

Если принять Р1 = 2Р, q1 = 2Р/ l, l1 = 0,5l, q = Р/ l, то NA = P, NB = 2P.

В соответствии с выражением (3.1) нормальная сила на участке АВ меняется по линейному закону. На рис. 3.3,а показана эпюра (график) нормальных сил на выделенном участке бруса.

Рис. 3.3

Рассмотрим равновесие элемента бруса длиной dz (рис. 3.3,б):

-N – qdz + (N + dN ) = 0.

После преобразований получим дифференциальную зависи-

36

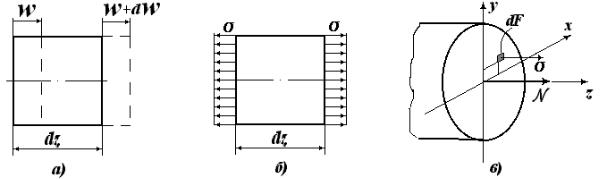
Из этого выражения следует, что величина q = const определяет угол наклона прямой на эпюре N (см.рис. 3.3,а). Если распределенная нагрузка на участке отсутствует (q=0), то нормальные силы на этом участке не меняются, т.е. N = const (рис. 3.3,в). Отметим, что величина скачка на эпюре N равна значению сосредоточенной силы 4P, приложенной в сечении.

В общем случае для эпюры нормальных сил соблюдается прави-

ло скачков: в том сечении, где приложена сосредоточенная сила на эпюре N имеет место скачок на величину этой силы.

Изменение сечения бруса не влияет на величину N.

3.2. Основные зависимости при растяжении

Для решения любой задачи деформируемого тела (бруса) должны быть получены три типа зависимостей.

Кинематические зависимости связывают деформации и пере-

мещения при рассмотрении деформирования элемента бруса. В сопротивлении материалов эти зависимости, как правило, получаются с использованием гипотезы плоских сечений (гипотезы Бернулли).

Физические зависимости связывают напряжения и деформации (закон Гука).

Статические зависимости связывают напряжения и усилия в сечении бруса (уравнения равновесия).

Рассмотрим получение этих зависимостей при растяжениисжатии бруса.

Кинематические зависимости получим при рассмотрении деформирования выделенного элемента бруса длиной dz (рис. 3.4,а).

Рис. 3.4

В соответствии с гипотезой Бернулли левое сечение, оставаясь плоским, переместится на величину w, а правое сечение - на w + dw. Изменение длины элемента ∆ (dz) =(w + dw) – w = dw. Тогда линейная деформация ε =∆ (dz)/dz в пределах элемента равна:

37

Равнодействующая всех элементарных сил σ dF в сечении равна нормальной силе N (рис. 3.4,в). В итоге для всего сечения получим:

Как правило, придерживаются следующей схемы преобразования полученных зависимостей. С использованием кинематической зависимости (3.4) закон Гука записывается в виде:

Это выражение используется в статической зависимости (3.6):

Дифференциальное уравнение (3.8) используется для определения перемещений сечений бруса.

Подставляя (3.8) в выражение (3.7), получим:

Эта формула может быть получена и непосредственно из зависимости (3.6) с учетом равномерного распределения нормальных напряжений по сечению (σ = const, см. рис. 3.4,б).

Отметим, что формула (2.6) является частным случаем формулы (3.9) при N = Р и использовалась только для определения напряжений при растяжении образца.

3.3. Перемещения сечений стержня

Продольные перемещения сечений стержня определяются интегрированием дифференциального уравнения (3.8):

38

где wo - постоянная интегрирования (перемещение сечения при z=0). Если учесть, что ε = σ /E = N/EF, то выражение (3.10) может быть

записано в виде:

Это выражение может быть получено и непосредственно интегрированием уравнения (3.4).

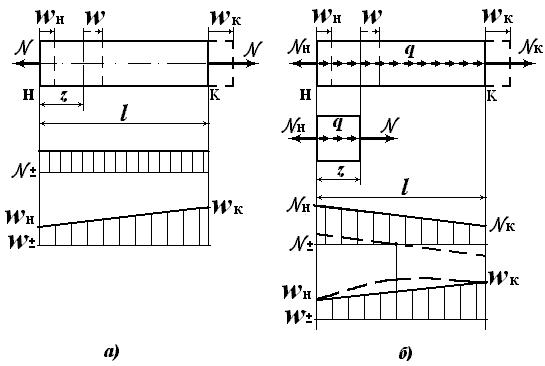
Часто необходимо определять перемещение wк концевого (к) сечения участка стержня, зная перемещение wн начального (н) сечения. Например, необходимо определить перемещение wк концевого сечения участка, на котором ε =N /EF = const (рис. 3.5,а). Воспользовавшись формулой (3.11) при wo = wн, получим:

где ∆ l - изменение длины участка.

Выражение для ∆ l может быть получено и из формулы (2.1), так как деформированное состояние участка бруса такое же, как рабочей части образца.

39