Деформация является безразмерной величиной. Положительная линейная деформация (деформация растяжения) соответствует увеличению длины отрезка, отрицательная линейная деформация (деформация сжатия) - уменьшению длины отрезка, положительная угловая деформация - уменьшению прямого угла (переходу его в острый угол). Совокупность линейных и угловых деформаций во всех направлениях и плоскостях, проходящих через точку, характеризует

деформированное состояние в точке.

Примечания.

1. Силы, напряжения, перемещения являются векторными величинами. В дальнейшем для упрощения записи и рисунков черточки для обозначения векторов не ставятся.

2. Следует иметь в виду, что термин «деформация» часто употребляется в двояком смысле. Во-первых, как физическая величина (линейная и угловая деформация). Во-вторых, как синоним деформирования; в этом смысле существуют понятия простейших видов деформации бруса - растяжение и сжатие, срез, кручение, изгиб.

1.5. Закон Гука. Основные принципы

Проводя опыты над различного типа пружинами, стержнями и нитями, английский учёный Р. Гук пришёл к выводу, что при их нагружении и при упругих деформациях в материале перемещения пропорциональны величине действующей силы δ =kP. Эта зависимость получила название закона Гука. Однако коэффициент пропорциональности k зависит как от свойств материала, так и от геометрических параметров системы. В современной трактовке закон Гука ус-

танавливает линейную или прямо пропорциональную зависимость между напряжениями и деформациями в точке тела. Коэффициент пропорциональности зависит только от свойств материала. Таким образом, закон Гука отражает свойства идеальной упругости материала.

Тела (системы), для которых выполняется закон Гука, называются линейно упругими. Системы, для которых зависимость между напряжениями и деформациями является нелинейной, называются физически нелинейными. Если выполняется закон Гука для материала, но зависимость между перемещениями и силами является нелинейной (при относительно больших перемещениях), то система называется

геометрически нелинейной. В общем случае, для нелинейных систем

могут присутствовать нелинейности обоих типов - физическая и геометрическая.

14

В механике деформируемых тел при анализе расчётной модели используются три основных принципа: принцип начальных размеров, принцип суперпозиции и принцип Сен-Венана.

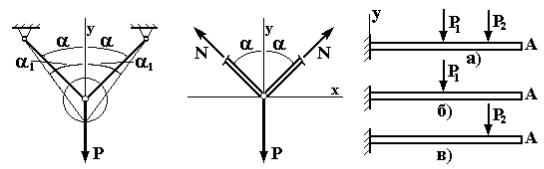
Согласно принципу начальных размеров для упругих систем, в которых перемещения малы, уравнения статики (равновесия) можно составлять для недеформированного состояния. Смысл принципа показан на примере стержневой системы (рис. 1.9). Применяя метод сечений и составляя уравнение равновесия для отсечённой части системы при α 1≈α

можно достаточно просто найти внутренние силы в упругих элементах (стержнях). Принцип начальных размеров неприменим для гибких систем, в которых имеют место большие перемещения, и для кинематически изменяемых систем, допускающих перемещение системы как жёсткого целого.

В соответствии с принципом суперпозиции (принципом незави-

симости действия сил) эффект от действия нескольких сил равен суммарному эффекту от раздельного действия каждой силы. При этом величина искомых параметров (перемещений, внутренних сил и т.д.) не зависит от порядка приложения внешних сил. Например, вертикальное перемещение концевого сечения (vA) консольной балки при совместном действии сил Р1 и Р2 (рис. 1.10,а) равно алгебраической сумме перемещений при действии каждой силы (рис 1.10,б,в):

vA (P1, P2) = vA (P1) + vA (P2).

Принцип суперпозиции справедлив только для систем, которые подчиняются закону Гука и принципу начальных размеров.

Принцип Сен-Венана устанавливает, что особенности приложения нагрузки не сказываются в упругом теле на расстояниях, превышающих характерные поперечные размеры. Например, если рассматривать случаи действия на малой площадке различных распределён-

15

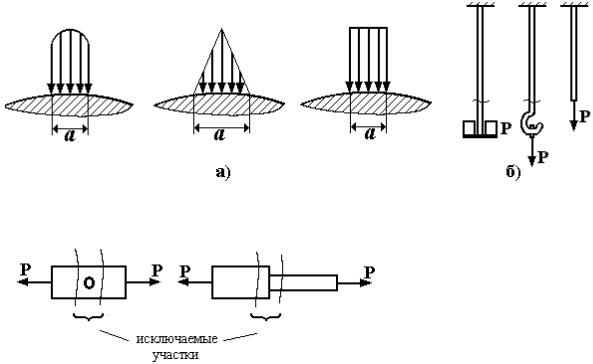
ных нагрузок (рис. 1.11,а), причём равнодействующие этих поверхностных нагрузок одинаковые, то отличаться будут местные напряжения и деформации в пределах малой области. При удалении от места приложения нагрузки, на расстоянии порядка размера а площадки нагружения (см. рис. 1.11,а), напряжения и деформации будут практически одинаковы. Нагрузки, имеющие одинаковые равнодействующие усилия, называются статически эквивалентными. Таким образом, применяя принцип Сен-Венана, можно не учитывать особенности приложения внешних сил, но вне зоны их действия. Например, при расчёте троса на растяжение не играет роли способ приложения нагрузки: за счет подвески грузов или тяги через крюк (рис. 1.11,б). Отбрасывая части троса, примыкающие к его концам, и прикладывая статически эквивалентную нагрузку P, получаем единую расчётную модель стержня (см. рис. 1.11,б).

Рис. 1.11

Принцип Сен-Венана распространяется и на тела, имеющие области резкого изменения геометрической формы. Например, брус с отверстиями, зоной ступенчатого измене-

ния сечения (рис. 1.12).

Рис. 1.12

В приближённых методах расчета, применяемых в сопротивлении материалов, часто используется гипотеза плоских сечений (гипотеза Бернулли): сечения бруса, плоские до деформации, остаются плоскими и после деформации. Эта гипотеза хорошо соблюдается, за исключением зон возмущения, оговариваемых принципом СенВенана.

16