1. Основные понятия
1.1. Моделирование реального объекта
Реальные объекты (конструкции) обладают большим многообразием своих характеристик, учесть которые в полном объёме невозможно. Для анализа реального объекта используется соответствующее физическое и математическое представление (моделирование), чаще всего конструктивных элементов, т.е. создаётся расчётная мо-
дель (или расчётная схема).
Моделирование осуществляется за счет некоторой схематизации реальной конструкции, включающей три основных направления: материал, геометрическая форма, нагрузки и связи.
Моделирование материала
Инженерные модели используют гипотезу сплошности среды: материал считается непрерывной средой, заполняющей весь объем тела. При этом материал наделяется некоторыми осреднёнными, среднестатистическими свойствами, не зависящими от микроструктуры материала.
К наиболее распространённым свойствам материала относятся однородность, изотропность, упругость, пластичность. Однородность - независимость свойств материала от величины и местоположения выделенного из тела объема. Такая схематизация свойств материала основана на том, что размеры рассматриваемых тел (или их частей) значительно превосходят размеры структурных элементов (например, кристаллических зерен), где проявляются особенности строения материала. Изотропность - одинаковость свойств материала во всех направлениях. Упругость - способность тела восстанавливать первоначальные форму и размеры после снятия нагрузки. Пластичность - способность тела не восстанавливать (частично или полностью) первоначальные форму и размеры после снятия нагрузки. При этом в теле появляются остаточные (пластические) деформации.
Существуют и анизотропные материалы, в которых свойства материала неодинаковые по различным направлениям. Различают естественную анизотропию (например, дерево) и искусственную (например, фанера, ткани и. т. д.). Получение искусственно анизотропных материалов является очень перспективным направлением создания новых материалов, обладающих необходимыми свойствами. Одним из таких направлений является создание так называемых компо-
зиционных материалов (композитов), соединяющих в себе относи-
6
тельную легкость, высокую прочность и жёсткость как наиболее полезные качества для силовых элементов конструкций. Композиты состоят из наполнителя (армирующего материала) и связующего (матрицы). Наполнителем являются волокна из различных материалов (углеродные, стеклянные, борные, органические, металлические и др.). В качестве связующего чаще всего используются полимерные материалы (эпоксидные, полиэфирные, фенольные смолы), а также и металлические (алюминиевые, титановые, стальные) или керамические материалы. Подбирая определенные компоненты «волокно - связующее», по-разному ориентируя волокна, используя различную технологию изготовления композитов, можно получить материалы с требуемыми свойствами, максимально соответствующими проектируемым конструкциям.
Геометрическое моделирование тел
В расчётном анализе используются три геометрические модели тела: брус (стержень), оболочка и пространственное (массивное) тело.
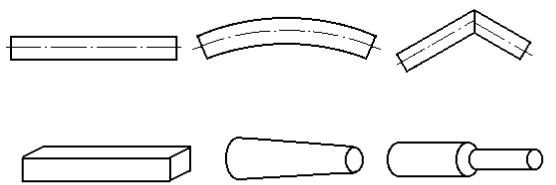
Брус - модель тела, длина которого существенно превышает поперечные размеры. Модели бруса различаются в зависимости от формы оси (рис. 1.1): а) прямолинейный, б) криволинейный, в) ломаный брус; в зависимости от изменения поперечного сечения бруса по длине (рис. 1.2): а) брус постоянного сечения, б) брус переменного сечения, в) ступенчатый брус. Естественно, отмеченные характерные признаки могут сочетаться, например криволинейный брус переменного сечения. Брус и конструкции, состоящие из элементов в виде бруса (стержневые системы), являются основными объектами изучения в сопротивлении материалов.
а) |
б) |
в) |
|
Рис. 1.1 |
|
а) |
б) |
в) |
|
Рис. 1.2 |
|
Оболочка - модель тела, толщина которого намного меньше других размеров. Оболочки как тонкостенные конструкции различаются, главным образом, формой срединной поверхности (цилиндрическая,
7
сферическая, коническая оболочки и т. д.), могут быть постоянной и переменной толщины. Оболочки широко применяются в различных областях техники, т.к. способны наиболее эффективно выполнять различные функции (прочностные, технологические, эксплуатационные, эстетические) в сочетании с малой материалоемкостью конструкций. Часто оболочки выполняются в совокупности с силовыми элементами в виде бруса (подкрепленные оболочки), оболочечные конструкции могут состоять и из нескольких оболочек различной формы. В частном случае, когда поверхность является плоскостью, оболочка вырождается в пластинку. Оболочки и оболочечные конструкции в основном изучаются в теории оболочек и специальных курсах строительной механики различных конструкций.
Модель пространственного тела имеет соизмеримые размеры. Методы расчета таких моделей рассматриваются в теории упругости.
Брус, оболочка и пространственное тело рассматриваются также как одномерная, двухмерная и трёхмерная модели тела в соответст-
вии с математическим описанием таких моделей.
Моделирование нагрузок и связей
Нагрузки являются мерой внешнего воздействия на рассматриваемый объект (тело) со стороны окружающих его тел или среды. Нагрузки моделируются системой внешних сил, которые разделяются на объемные и поверхностные силы. Объемные силы распределены по объему тела, приложены к каждой его частице (силы тяжести, инерции, магнитного взаимодействия). Поверхностные силы действуют на участках поверхности тела (силы воздействия среды, контактного взаимодействия тел и т.д.). При моделировании нагрузки вводятся понятия сосредоточенных силы и момента (пары сил), распределенной (погонной) нагрузки.
Под сосредоточенной силой Р (рис. 1.3,а) понимается равнодействующая поверхностных сил, действующих на относительно малой площадке поверхности тела (площадка условно стягивается в точку). Аналогично, сосредоточенный момент М может рассматриваться как статический эквивалент поверхностных сил, некоторые варианты распределения которых показаны на рис. 1.3,б. Распределенная нагрузка q (рис. 1.3,в) получается приведением поверхностных сил к линии действия (площадка нагружения условно стягивается в линию). Распределенная нагрузка может быть постоянной или переменной интенсивности.
8
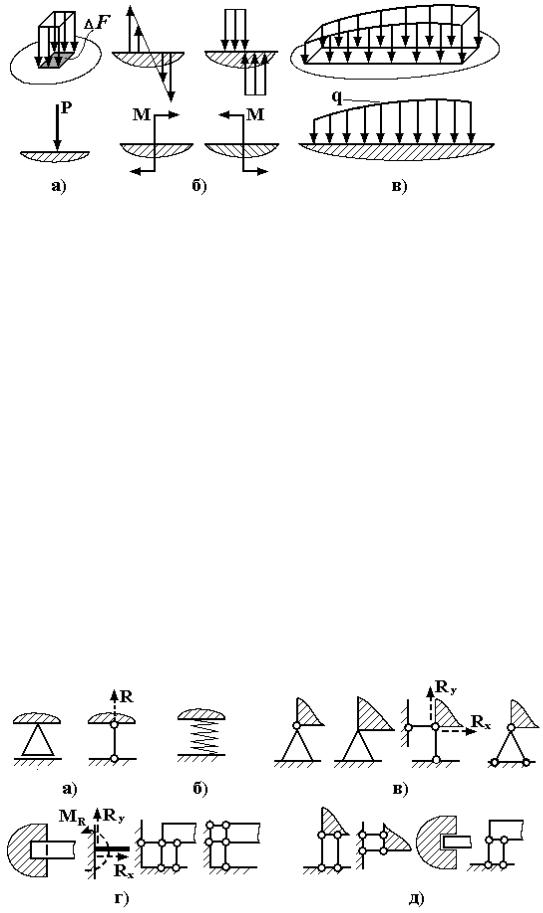
Рис. 1.3
В системе СИ единицами измерения силы являются ньютоны (Н) или килоньютоны (кН), т.е. применяется такая размерность для рассматриваемых типов нагрузки: Р /Н, кН/; М /Н м, кН м/; q /Н/м, кН/м/.
В расчетной модели используется понятие связи как ограничения перемещений в некоторых точках тела. Наиболее часто рассматриваются модели типовых опор как системы связей. В качестве примера на рис. 1.4 показаны плоские модели опор. Шарнирно-подвижная опора или каток (рис. 1.4,а) накладывает одну связь (на рисунке это соответствует запрещению вертикального перемещения). В частности, такая связь может быть упругой (рис. 1.4,б), допускающей определённые (конечные) перемещения. Шарнирно-неподвижная опора моделируется двумя связями (рис. 1.4,в), которые запрещают любые линейные перемещения в плоскости. Опора типа жёсткого закрепления или заделки (рис. 1.4,г) запрещает линейные и угловые перемещения. Возможны и другие варианты опор за счёт наложенных связей, например подвижная заделка - закрепление, ограничивающее поворот и линейное перемещение в направлении наложенных связей
(рис. 1.4,д).
Рис. 1.4
9