8. Сложное сопротивление бруса

Ранее рассматривались простейшие виды деформации бруса, при которых от действия определённых нагрузок в поперечных сечениях бруса возникали отдельные внутренние силовые факторы: растяжение и сжатие (N), кручение ( M к), прямой изгиб ( M и Q). Однако в других случаях нагружения в поперечных сечениях бруса могут возникать различные сочетания внутренних силовых факторов (в общем случае - все шесть). Такая сложная деформация бруса называется

сложным сопротивлением. Используя принцип суперпозиции, слож-

ное сопротивление бруса может быть представлено как сумма простых видов деформации. Особо оговаривается лишь случай бруса относительно большой жёсткости при действии сжимающей силы, чтобы исключить возможность потери устойчивости бруса (см. часть II). Чаще всего рассматривают специальные случаи сложного сопротивления бруса: косой изгиб, косой изгиб с растяжением (сжатием), внецентренное растяжение (сжатие), изгиб с кручением.

8.1. Косой изгиб

Косой изгиб возникает в случае действия поперечной нагрузки (P, M, q) в плоскости, проходящей через ось бруса и не совпадающей ни с одной из главных плоскостей инерции. Плоскость действия на-

грузки называется силовой плоскостью. Главной плоскостью инерции

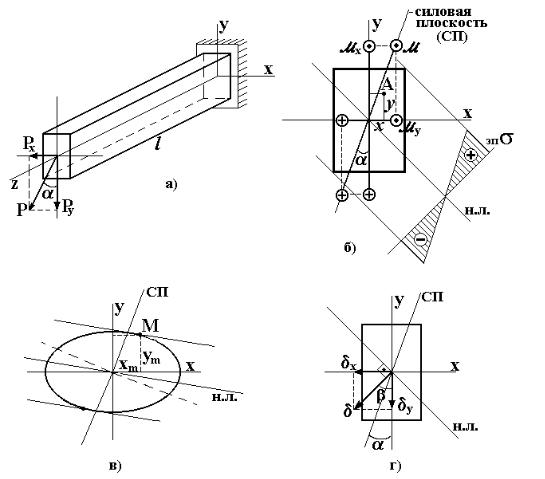
называется плоскость, в которой расположены соответствующие главные оси инерции всех поперечных сечений бруса. В общем случае таких плоскостей две. Например, для призматического консольного бруса (рис. 8.1,а) - вертикальная (Оyz) и горизонтальная (Оxz) плоскости.

Примечание. Исключение составляет брус, имеющий сечение в виде круга или правильного многоугольника. Для такого бруса никогда не будет косого изгиба.

Рассмотрим особенности косого изгиба на примере консольной призматической балки, нагруженной силой P в торцевом сечении под углом α к оси y (см. рис. 8.1,а). Разложим силу P на составляющие Px и Py по осям:

Каждая из этих сил действует в одной из главных плоскостей инерции и вызывает прямой изгиб. Используя принцип суперпозиции, представим косой изгиб как сумму двух прямых изгибов. Опасное сечение - в заделке, где расчётные значения изгибающих моментов от сил Px и Py равны:

Откуда, учитывая соотношения (8.2), получаем уравнение нейтральной линии при косом изгибе:

Нейтральная линия проходит через центр сечения и расположена в квадрантах, противоположных тем, где расположена линия силовой плоскости (рис. 8.1,б). Из условия Jx≠Jy следует, что нейтральная ли-

ния не перпендикулярна силовой плоскости. При этом нейтральная линия повёрнута от направления, перпендикулярного силовой плоскости, в сторону главной оси минимального момента инерции. Соответственно, при Jx=Jy невозможен косой изгиб, т.к. все центральные оси сечения являются главными (всегда имеет место прямой изгиб).

Зная положение нейтральной линии, можно построить эпюру нормальных напряжений в сечении (эп.σ на рис. 8.1,б). Максимальные напряжения возникают в точках, наиболее удалённых от нейтральной линии (xm, ym - координаты такой точки):

Для сечения произвольной формы координаты xm, ym обычно определяются графическим образом для точек касания контура сечения линиями, параллельными нейтральной линии (рис. 8.1,в). Для сечений, имеющих наружные угловые точки и две плоскости симметрии (прямоугольник, двутавр и т.д.) xm=xmax, ym=ymax, максимальные напряжения определяются согласно формул (8.5) и (6.8) наиболее просто, используя моменты сопротивления сечения относительно осей x, y

(Wx=Jx/ymax, Wy=Jy/xmax):

Из формулы (8.6) видно, что при косом изгибе могут значительно увеличиваться нормальные напряжения в балках, имеющих сечения с существенно различными моментами сопротивления (например, двутавр, швеллер, для которых Wx >> Wy).

Касательные напряжения при косом изгибе играют такую же второстепенную роль, как и при прямом изгибе. При косом изгибе величина полных касательных напряжений в определённой точке сечения находится как геометрическая сумма компонент τ x и τ y:

τ = ττ 2x++ ττ 2y .