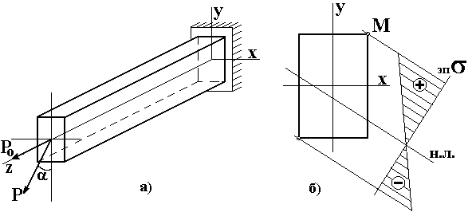
Рис. 8.2

Таким образом, нейтральная линия не проходит через начало координат в сечении. Как следствие, наибольшие растягивающие и сжимающие напряжения получаются различной величины для любого сечения. Эпюра нормальных напряжений в сечении (эп.σ ) показана на рис. 8.2,б. Максимальные напряжения определяются для точки, наиболее удалённой от нейтральной линии (координаты xm, ym т.М на рис. 8.2,б):

8.3. Внецентренное растяжение (сжатие)

Внецентренным растяжением (сжатием) называется деформа-

ция бруса при действии двух равных и противоположно направленных сил по линии, параллельной оси бруса и не совпадающей с ней

(рис. 8.3,а).

В любом поперечном сечении бруса возникают следующие внутренние силовые факторы (на рис. 8.3,б изображение нормальной силы N соответствует внецентренному растяжению):

где xp, yp - координаты точки приложения силы P в торцевом сечении.

(Расстояние от точки приложения силы до центра сечения называется

эксцентриситетом.)

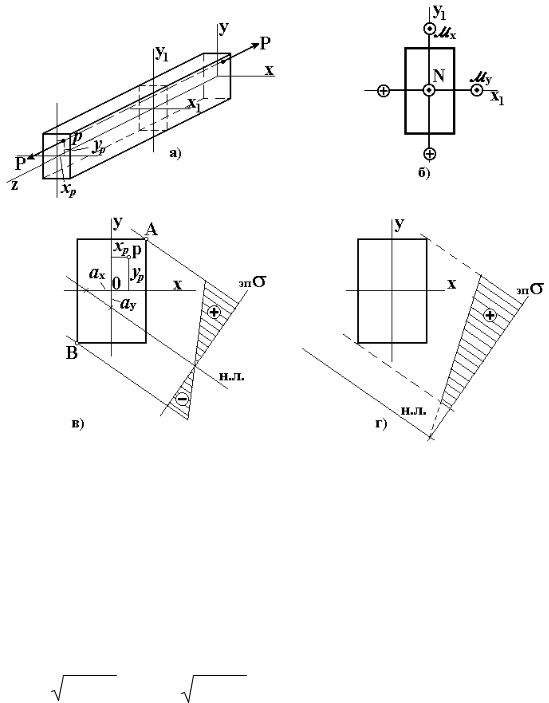
Рис. 8.3

Таким образом, внецентренное растяжение (сжатие) можно рассматривать как частный случай совместной деформации косого изгиба и осевого растяжения (сжатия). Подставляя формулы (8.11) в (8.8), получим выражение для нормальных напряжений в произвольной точке сечения:

тельно главных осей.

При внецентренном сжатии первое слагаемое в выражении (8.12) подставляется со знаком минус, т.к. N = − P.

Положение нейтральной линии определяется из условия σ (x,y)=0.

Тогда из выражения (8.12) получаем уравнение нейтральной линии:

Нейтральная линия в сечении не проходит через начало координат (центр сечения). Для её построения удобно использовать отрезки,

отсекаемые нейтральной линией на координатных осях: ax=-iy2/xp,

ay=-ix2/yp (рис. 8.3,в). Если xp > 0, yp > 0, то отрезки ax < 0, ay < 0, т.е.

нейтральная линия расположена по другую сторону от центра сечения, чем точка приложения силы P (полюс р). Эпюра нормальных напряжений в сечении (эп.σ ) показана на рис. 8.3,в. Чем ближе сила P к оси бруса, тем дальше уходит нейтральная линия от центра сечения. При некотором положении силы P нейтральная линия может быть расположена вне сечения (рис. 8.3,г): тогда во всех точках сечения возникают напряжения одного знака.

Как обычно, опасными являются точки, наиболее удалённые от нейтральной линии. Зная их координаты (xm, ym), определяются максимальные напряжения из формулы (8.12):

Для сечения с выступающими угловыми точками формула (8.14) упрощается:

Для бруса из материала, по-разному сопротивляющегося растяжению и сжатию, следует определять максимальные растягивающие и сжимающие напряжения (например, в т.А и т.В сечения на рис. 8.3,в):

Отметим практические случаи возникновения внецентренного растяжения (или сжатия) бруса:

1) конструктивные элементы с эксцентрично приложенной нагрузкой;

2)конструктивные элементы с односторонними вырезами при осевой нагрузке;

3)стержни с начальным прогибом.

Во всех случаях необходимо проводить расчёты на прочность, т.к. напряжения при внецентренном растяжении (сжатии) всегда больше, чем при чисто осевой деформации за счёт дополнительной деформации изгиба. Особенно это касается элементов конструкций из хрупких материалов (бетон, кирпич), для которых недопустимы рас-

тягивающие напряжения из-за низкой прочности таких материалов при растяжении.

8.4. Расчёт на прочность при сложном сопротивлении бруса

Расчёт на прочность для рассмотренных случаев сложного сопротивления бруса проводится так же, как и при прямом изгибе балки (см. формулы (6.12) и (6.14) раздела 6.5). Основными являются нормальные напряжения, для которых и записывается условие прочности.

Для бруса из пластичного материала (как правило, σ тр≈σσ тс) усло-

где максимальные напряжения σ max для бруса определяются по фор-

мулам (8.5), (8.6), (8.10), (8.14), (8.15).

Для бруса из хрупкого материала, по-разному сопротивляющегося растяжению и сжатию, записываются два условия прочности:

При этом, используя вышеуказанные формулы для σ max, необходимо отдельно определять максимальные растягивающие и сжимающие напряжения. Условия прочности (8.18) часто используются в расчётах элементов строительных сооружений (колонн, стен и др.) при их внецентренном сжатии.