
- •Сопротивление материалов
- •Содержание
- •Введение
- •Основные понятия
- •1.1 Моделирование реального объекта
- •1.2 Внутренние силы. Метод сечений
- •1.5 Закон Гука. Основные принципы
- •2. Механические свойства материалов
- •2.3 Испытание на сжатие
- •2.4 Влияние различных факторов на механические свойства материалов
- •3.1 Определение нормальных сил
- •3.2 Основные зависимости при растяжении
- •3.4 Учет факторов, влияющих на изменение длины стержня
- •3.5 Расчет стержня на прочность
- •4. Кручение
- •4.1 Чистый сдвиг
- •4.2 Кручение бруса круглого сечения
- •4.4 Расчет валов на прочность и жесткость
- •4.5 Характер разрушения валов
- •4.8 Кручение тонкостенного стержня открытого профиля
- •4.9 Расчет витых цилиндрических пружин с малым шагом
- •5.1 Статистические моменты сечения
- •5.2 Моменты инерции сечения
- •6. Изгиб
- •6.2 Основные зависимости при чистом изгибе
- •6.3 Нормальные напряжения при изгибе
- •6.5 Напряжения при поперечном изгибе
- •6.8 Балки равного сопротивления изгибу
- •7.1 Основные определения
- •7.2 Расчет плоских систем
- •7.3 Моделирование связей
- •8. Сложное сопротивление бруса
- •8.1 Косой изгиб
- •8.3 Внецентренное растяжение (сжатие)
- •Приложение 1
- •Приложение 2
- •Список дополнительной литературы
6.3. Нормальные напряжения при изгибе
Подставляя зависимость (6.6) в формулу (6.5), получаем выраже-
ние для нормальных напряжений в произвольной точке поперечно-
го сечения:
σ = |
M y |
. |
(6.7) |
|
|||
|
Jx |
|
|
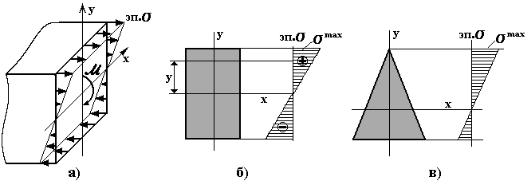
Выражение (6.7) определяет закон изменения нормальных напряжений в плоскости сечения - линейная зависимость от координаты у
(рис. 6.6,а).
Рис. 6.6
Максимальные нормальные напряжения в сечении возникают в точках, наиболее удалённых от нейтральной линии:
σ m ax = |
M ym ax |
== |
M |
, |
(6.8) |
|
|
||||
|
Jx |
W x |
|
||
где Wx - момент сопротивления сечения при изгибе:
W x = |
Jx |
. |
(6.9) |
|
|||
|
ym ax |
|
|
Условно эпюра σ (y) изображается в плоскости сечения (рис. 6.6,б,в). Знаки напряжений на эпюре ставятся в зависимости от направления изгибающего момента M в сечении (на рис. 6.6,б знаки показаны для момента отрицательного направления). Если сечение несимметричное относительно нейтральной линии, то максимальные растягивающие и сжимающие нормальные напряжения будут различной величины (см. рис. 6.6,в).
Момент сопротивления Wx для сечений различной формы определяется через момент инерции Jx сечений (см. раздел “Геометрические характеристики сечений”). Например, для типовых сечений получим:
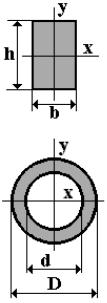
• прямоугольное сечение со сторонами b и h:
J = |
|
bh3 |
; y |
|
= |
|
h |
; |
W |
= |
|
|
bh2 |
; |
|
|
||
|
|
|
|
|
|
|||||||||||||
x |
12 |
|
m ax |
|
2 |
|
|
x |
|
6 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
• кольцевое сечение (α |
= |
d |
): |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
Jx = πD 4 |
(1−− α |
4 )≈≈ |
0,05D 4 (1−−αα |
4 ); |
|
|
ym ax = |
D |
; |
|||||||||
|
|
|
||||||||||||||||
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
W x = πD 3 (1−− α 4 )≈≈ 0,1D 3(1−− αα 4 ); |
||||||||||||||||||
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• сплошное круглое сечение (d=0, α |
|
= 0): |
|
|
||||||||||||||
Jx = |
πD 4 |
≈≈ |
0,05D 4; |
|
W x = |
πD 3 |
≈≈ |
|
0,1D 3. |
|||||||||
|
64 |
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
||
6.4. Рациональные формы сечения балок при изгибе
Напряжения в сечении балки распределяются неравномерно. Поэтому встаёт вопрос о проектировании балок рациональной формы сечения, обеспечивающих наилучшим образом использование материала. Вопрос в том, как обеспечить заданную прочность балки при возможно минимальной ее материалоемкости. А эти факторы зависят от характеристик сечения - Wx и F. Рациональными формами сече-
ний балок при изгибе считаются такие, которые при заданной площади F обеспечивают наибольшую величину момента сопротивления Wx (или при минимальной площади F обеспечивают заданную величину Wx). Качественным показателем рациональности сечения может служить величина Wx/F: чем она больше, тем более рациональное сечение.
Оптимально было бы использование материала только в области наибольших напряжений, т.е. распределять материал подальше от нейтрального слоя. Так как в сечении балки при изгибе возникают напряжения разного знака, то выбор рационального профиля зависит и от материала.
Пластичные материалы чаще всего имеют одинаковые (или близкие по величине) прочностные характеристики на растяжение и сжатие (σ тр≈ σ тс). Поэтому для балок из пластичных материалов рационально использовать сечения, симметричные относительно нейтральной линии. А идея периферийного распределения материала привела на практике к созданию стандартных профилей в виде двутавра и швеллера (рис. 6.7). Наибольшие значения параметра Wx/F у двутав-
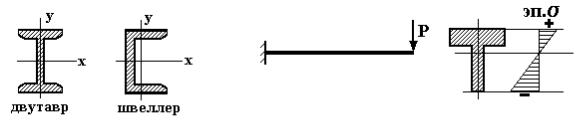
ра. Основываясь на таком подходе, можно убедиться, что лучше применять балки не сплошного круглого сечения, а кольцевого; не прямоугольного сечения, а коробчатого.
Рис. 6.7 Рис. 6.8
Для балок из материалов, неодинаково работающих на растяжение и сжатие, выгодным является применение сечений, несимметричных относительно нейтральной линии. Причём положение нейтраль-
ной линии |
желательно иметь таким, чтобы выполнялось условие |
σ pmax/σ cmax |
= σ вp/σ вc. При этом важна правильная ориентация сече- |
ния в зависимости от положения растянутых и сжатых волокон. Например, для консольной чугунной балки таврового сечения (рис. 6.8) при показанном направлении нагрузки необходимо расположить балку полкой вверх, т. к. в этом случае будет σ cmax > σ pmax, а для чугуна
σвc > σ вp.
6.5.Напряжения при поперечном изгибе
При поперечном изгибе в сечениях балки возникают не только нормальные σ , но и касательные τ напряжения. Поперечная сила Q в сечении является результирующим силовым фактором от действия вертикальной составляющей τ касательных напряжений: Q = ∫ τ dF .
F
В результате возникающей деформации сдвига γ поперечные сечения не остаются плоскими, а искривляются. Кроме того, действие поперечной нагрузки, в частности распределенной q(z), приводит к взаимодействию продольных слоёв балки. Таким образом, строго говоря,
при поперечном изгибе балки не соблюдаются гипотезы 1 и 2, приня-
тые при чистом изгибе. Однако экспериментальные результаты, а также сопоставление с более строгим решением по теории упругости показывают, что несоблюдение отмеченных гипотез при поперечном изгибе приводит к несущественной погрешности при использовании формул чистого изгиба. Поэтому и при поперечном изгибе используются соотношения (6.6) для кривизны оси изогнутой балки и соотношения (6.7), (6.8) - для нормальных напряжений:
σ |
= |
M y |
; σ |
m ax |
= |
M |
. |
Jx |
|
W x |
|||||
|
|
|
|
|
|
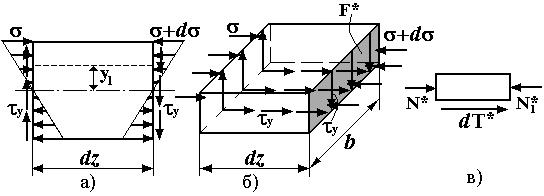
Для определения касательных напряжений τ в произвольной точке сечения используется гипотеза 3 (τ = const по ширине сечения) и закон парности касательных напряжений. Выделим элемент балки (рис. 6.9,а) (берётся участок балки, где q = 0, т.к. учёт распределённой нагрузки q приводит к появлению членов второго порядка малости, которыми можно пренебречь) и рассмотрим верхнюю часть этого элемента, отсеченную продольной плоскостью y1 = const (рис. 6.9,б).
Рис. 6.9
На отсечённую часть в поперечных сечениях действуют нормальные напряжения (σ +dσ ), σ и касательные напряжения τ , а в продольном сечении действуют такие же напряжения τ согласно закону парности касательных напряжений (Направление напряжений соответствует положительным направлениям M и Q Напряжения приведём к результирующим силам (рис. 6.9,в):
N * = ∫ σ dF ; N1* = |
∫ (σ ++ dσσ )dF ; |
dT* = τ bdz, |
(6.10) |
F* |
F * |
|
|
где F* - площадь отсечённой части поперечного сечения. |
|
||
Составим уравнение равновесия для отсечённой части балки: |
|||
∑ Fz = 0; - N1* + N*+ dT* = 0 или |
dT* = N1* - N*. |
|
|
После подстановки соотношений (6.10) в это уравнение и преобразований, а также с учетом дифференциального соотношения
dσ = |
|
dM y |
из (6.7), можно получить: |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||
|
|
Jx |
|
|
|
|
|
|
|
|
|
|
|
|
||
τ bdz= |
∫ dσσ dF = |
∫ |
dM ydF |
= |
dM |
∫ ydF или τ = |
1 dM |
∫ ydF*. |
||||||||
|
|
|
|
|
||||||||||||
|
Jx |
bJx dz |
||||||||||||||
|
|
F |
* |
|
F |
* |
Jx |
F |
* |
F |
* |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
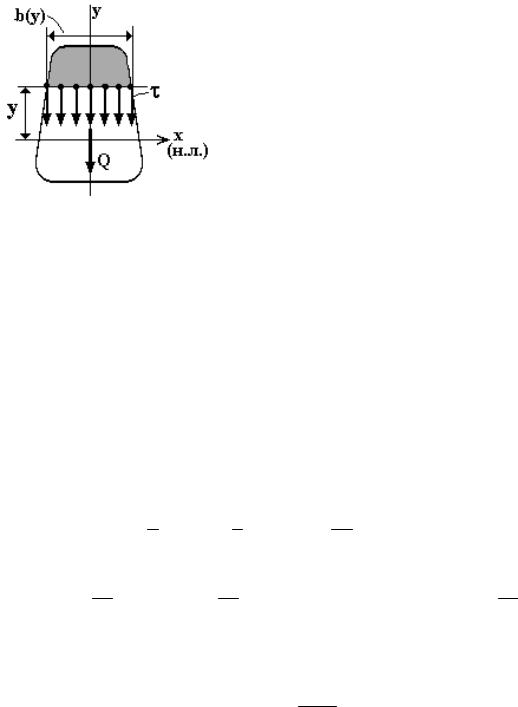
Учитывая, что ∫ ydF = S*x; |
dM |
= Q , |
|
||
F* |
dz |
|
|
|
|
окончательно получаем формулу для касательных напряжений в балках, которая носит название формулы Д.И. Журав-
ского:
|
τ = |
Q S*x |
, |
(6.11) |
|
|
|||
Рис. 6.10 |
|
Jxb |
|
|
где τ - вертикальная составляющая каса- |
||||
|
тельного напряжения; Q - |
поперечная |
||
сила в сечении балки; Jx - момент инерции сечения относительно нейтральной линии; b = b(y) - ширина сечения на уровне y, где определяются касательные напряжения (по ширине сечения они постоянны); Sx*=Sx*(y) - статический момент отсеченной части сечения (расположенной выше или ниже уровня y) (рис. 6.10). Направление касательных напряжений τ в поперечном сечении балки соответствует направлению поперечной силы Q в этом сечении.
Для примера рассмотрим балку прямоугольного сечения со сторонами b и h (рис. 6.11,а). В соответствии с формулой (6.11) изменяется только статический момент отсечённой части сечения:
|
|
|
S*x |
= F*y |
|
h |
|
|
|
1 |
|
h |
|
|
b |
h2 |
y12); =Jx |
|
bh3 |
|
|
|
|
|
||||||||
|
|
|
= |
b( − |
y |
) |
|
(+ |
y = ) |
|
|
|
(− |
|
|
|
; |
b(y= |
) b. |
|||||||||||||
|
|
|
|
2 |
12 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
c |
|
2 |
1 |
|
2 |
2 |
1 |
4 |
|
|
|
|
1 |
|
|
|
|
||||||||
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
τ |
|
|
Q b h2 |
|
2 |
|
6Q h2 |
2 |
|
|
|
ïðè y = 0 τ |
m ax 3 |
Q |
3 Q |
|||||||||||||||||
= |
|
|
|
|
|
( |
− |
y1 )= |
|
|
|
( |
|
− |
y1 ); |
è |
|
= |
|
|
|
|
= |
|
|
|
. |
|||||
|
bh3 |
|
|
|
bh3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
b 2 4 |
|
|
|
|
|
4 |
|
|
|
|
|
1 |
|
|
2 bh |
2 F |
|||||||||||||
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для круглого сечения радиуса R, выполнив аналогичные преобразования, можно получить:
τ (y ) = |
4Q |
(R |
2− y2); τ m ax= |
4Q = |
|
4 |
|
Q |
. |
|
|
|
|||||||
1 |
3πR4 |
|
1 |
3πR2 |
|
3 F |
|||
|
|
|
|||||||
На рис. 6.11а,б приведены эпюры касательных напряжений τ для прямоугольного и круглого сечений. В обоих случаях напряжения распределяются по высоте сечения по закону квадратичной параболы, максимальные напряжения возникают в точках нейтральной линии.
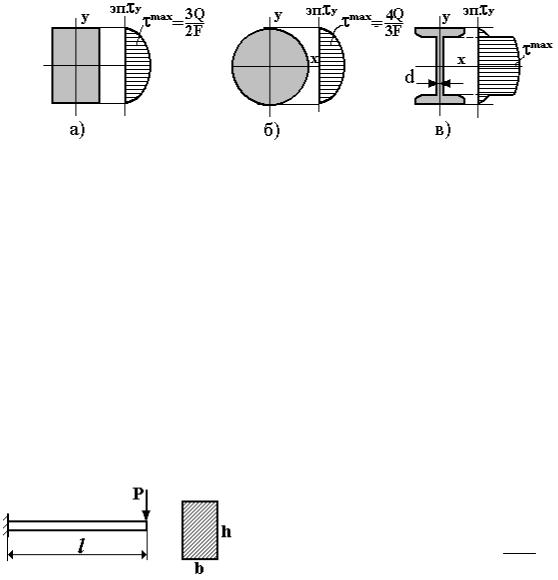
Рис. 6.11
Некоторые особенности в распределении касательных напряжений имеют место для тонкостенных профилей. Эпюра τ для двутаврового сечения показана на рис. 6.11,в. Вследствие резкого уменьшения ширины сечения возрастает величина касательных напряжений в стенке профиля. Максимальные напряжения равны τ max = QS*x/Jxd, а величины Jx, S*x, d приводятся в соответствующих таблицах ГОСТ сортамента. Приведенная эпюра τ y является приближенной, т. к. не учитывает местного увеличения напряжений вблизи входящего угла сечения, где стенка соединяется с полкой.
Можно сопоставить наибольшие касательные и нормальные напряжения в балках, чтобы выяснить определяющие напряжения при поперечном изгибе балок. Например, для консольной балки прямоугольного сечения (рис. 6.12) эти напря-
жения равны:
|
σ m ax = |
M m ax |
== |
|
|
|
|
Pl |
== |
6P2l; |
||||||||
|
|
|
|
|
|
2 |
||||||||||||
Рис. 6.12 |
|
|
W x |
|
|
|
bh |
/6 bh |
||||||||||
τ m ax = |
3 |
|
Q |
== |
|
3 |
|
P |
. |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 F |
|
2 bh |
|
|
|
|||||||||||
Сопоставляя полученные значения |
|
σ m ax |
= |
|
|
4 |
l |
и учитывая, что |
||||||||||
|
τ m ax |
|
|
|
h |
|
||||||||||||
для бруса l/h>10, можно сделать вывод, что для нетонкостенных балок максимальные нормальные напряжения значительно больше, чем касательные напряжения.
Следует отметить, что формула (6.11) позволяет вычислить напряжения не только в поперечных сечениях, но и в продольных (по закону парности касательных напряжений).
6.6. Расчет на прочность при изгибе
Для балок в большинстве практических случаев определяющими являются нормальные напряжения, а касательные напряжения играют второстепенную роль. Поэтому основным принимается условие проч-
ности по нормальным напряжениям, а условие прочности по касательным напряжениям является поверочным.
Для балок из пластичных материалов условия прочности имеют
вид:
σ m ax
τ m ax
≤ σ[ ]; |
σ [ ]= |
|
σ ò |
; |
(6.12) |
|
|
|
|||||
|
|
|
nò |
|
||
≤ [τ ]; |
τ[ ]= |
τ ò |
. |
(6.13) |
||
|
||||||
|
|
nò |
|
|||
Для балок несимметричного профиля, выполненных из хрупких материалов, вместо условий (6.12) необходимо составить два условия прочности:
|
|
[ ] |
|
|
|
σ |
|
|
|
|
|
|
|
|
||
p |
≤ σσ |
|
|
|
|
|
|
|
|
|
σ Bc |
|
|
|||
|
σ |
m ax |
p , ãäå |
[σ |
] |
= |
Bp |
; [σ |
] |
= |
. |
(6.14) |
||||
|
|
|
|
|
||||||||||||
σ |
c |
≤ σ[σ |
] |
|
p |
n |
|
|
c |
n |
|
|
|
|||
|
|
|
|
B |
|
|
|
B |
|
|||||||
|
m ax |
|
c |
|
|
|
|
|
|
|
|
|
||||
При расчете балок постоянного сечения наибольшие нормальные напряжения возникают в сечении, где действует максимальный изгибающий момент M max. В этом случае условие прочности (6.12) можно записать в виде:
Ì m ax |
≤ [σ ]. |
(6.15) |
|
||
W x |
|
|
Условие (6.15) используется для подбора сечения балки при изгибе:
W x ≥ |
M m ax |
. |
(6.16) |
|
|||
|
[σ ] |
|
|
При необходимости после этого проводится проверка по условию прочности (6.13) при Q = Qmax.
Для балок переменного сечения (Wx≡Wx(z) условие прочности (6.15) следует записать в таком виде:
|
Ì |
|
|
≤ [σ ]. |
|
|
|
|
|
(6.15*) |
|
|
|
||||
|
W |
x |
m ax |
|
|
В некоторых случаях при расчете балок на прочность следует обращать особое внимание на касательные напряжения в поперечных и продольных сечениях балок. В частности, когда рассматриваются:

а)
б)
Рис. 6.13
1) тонкостенные балки;
2)короткие балки из волокнистых ма-
териалов, имеющих малую прочность на скалывание вдоль волокон (например, возможно разрушение деревянного бруска по продольной плоскости, совпадающей с нейтральным слоем (рис. 6.13,а);
3)составные балки (рис. 6.13,б), для ко-
торых возможно разрушение по продольной плоскости контакта частей балки от действия максимальных касательных напряжений.
6.7. Перемещения в балках при изгибе
При расчёте конструкции вычисляются не только напряжения, но и перемещения. Причём методы определения перемещений играют важную роль как в общей оценке жёсткости конструкции, так и при решении многих прикладных задач (расчёт статически неопределимых систем, динамическое нагружение конструкций, колебания упругих систем и др.).
Дадим общие понятия о перемещениях в балках, рассматривая прямой изгиб балки. Для определённости принимается общая система координат Oyz (рис. 6.14), начало которой выбирается в центре площади какого-либо сечения, а ось z направлена по оси балки.
(При этом следует иметь в виду, что с каждым сечением связана местная система центральных осей, параллельных исходным.)
Для поперечных сечений
балок различают два вида перемещений:
1) прогиб v(z) - линейное перемещение сечения (центра площади сечения) в направлении, перпендикулярном оси балки;
2) угол поворота θ (z) - угловое перемещение сечения по отноше-
нию к первоначальному положению (поворот сечения относительно нейтральной линии).

Принимая, что положительное направление жительным направлением изгибающего момента ложительное направление оси Oy - вверх (см.
θ совпадает с поло- M в сечении, а порис.6.14), получим
tgθ = dv. В большинстве практических случаев перемещения в dz
балках относительно малы, так что можно считать tgθ ≈ θ . Поэтому дифференциальное соотношение между прогибом и углом поворота сечения получается в виде:
θ = v′ ; v′ = |
dv |
. |
(6.17) |
|
|||
|
dz |
|
|
Рассмотрим некоторые методы определения перемещений.
6.7.1. Дифференциальное уравнение упругой линии балки
Ось изогнутой балки часто называют упругой линией. В случае прямого изгиба балки, учитывая соотношения (6.3), (6.6) и (6.17), для определения перемещений можно использовать систему дифференциальных уравнений в виде:
dθ |
|
|
= |
|
|
M |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJx . |
|
|||||
dz |
|
(6.18) |
||||||||||
|
|
dv |
= θ |
|
||||||||
|
|
|
|
|||||||||
|
|
|
dz |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
Исключая второе уравнение из системы (6.18), получаем диффе- |
||||||||||||
ренциальное уравнение упругой линии балки: |
|
|||||||||||
|
d2v |
= |
|
M |
. |
(6.19) |
||||||
|
2 |
|
|
|||||||||
|
dz |
|
|
|
|
EJx |
|
|||||
Уравнение (6.19) (или система уравнений (6.18) может применяться для определения как перемещений отдельных сечений, так и формы оси изогнутой балки. Последовательным интегрированием уравнений в системе (6.18) или уравнения (6.19) получаем:
|
|
M dz |
|
|
M dz2 |
|
|
||
θ (z)= |
∫ |
|
++θθ ο; |
v(z)= |
∫ ∫ |
|
++ |
θ oz++ vo, |
(6.20) |
EJx |
EJx |
||||||||
|
z |
|
|
|
z z |
|
|
|
|
где θ o, vo - постоянные интегрирования, имеющие смысл перемещений сечения балки в начале координат (z = 0). Для балки постоянной жесткости EJx = const интегрирование упрощается:
θ (z)= |
1 |
∫ |
M dz++θθ o; v(z)= |
1 |
∫ ∫ |
M dz2++ θ o++ vo. (6.21) |
|
EJx |
EJx |
||||||
|
|
|
|||||
|
|
z |
|
|
z z |
|
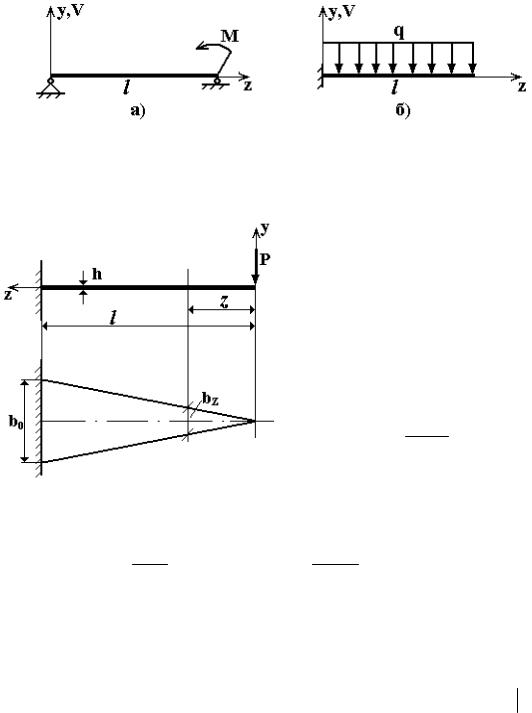
Постоянные θ o, vo определяются из граничных условий, число которых равно двум (порядку дифференциального уравнения). Граничные условия могут составляться для v и v′ = θ в зависимости от типа закрепления балки. Например, для шарнирно опертой балки (рис. 6.15,а) граничные условия имеют вид: v(0) = 0, v(l) = 0; для консоль-
ной балки (рис. 6.15,б): v(0) = 0, v′(0) = 0.
Рис. 6.15
Пример 6.1. Рассмотрим определение перемещений для консольной балки переменного сечения, нагруженной на свободном конце силой Р (рис. 6.16). Балка имеет постоянную толщину и переменную ширину сечения (h=const, b=var).
Выберем начало координат на свободном конце балки. Тогда:
M(z)=-P z; b(z)=boz/l,
где bo, l - ширина сечения в заделке и длина балки. Момент инерции произвольного сечения балки можно представить в таком виде:
|
b(z)h |
3 |
|
boh |
3 z |
z |
||||
Jx (z) = |
|
|
== |
|
|
|
|
== Jo |
|
, |
12 |
|
12 |
|
|
|
|||||
|
|
|
|
|
l |
l |
||||
ãäå Jo = boh3 .
12
Подставив полученые выражения в Рис. 6.16 дифференциальные уравнения (6.18) и выполнив интегрирование, получим такие
выражения:
|
|
|
|
|
2 |
|
|
|
θ (z) = − |
P lz+ |
θθ |
o |
; v(z) =− |
P lz+ |
θθ + z |
v |
. |
|
E Jo |
|
2E Jo |
o |
|
o |
||
|
|
|
|
|
|
|||
Граничные условия имеют вид θ (l) = 0, v(l) = 0. Подставив их в полученные выражения, находим константы интегрирования: θ o = Pl2/EJo; vo=-Pl3/2EJo. Тогда для функции прогибов по длине балки и величины максимального прогиба (в сечении z = l) получим следующие выражения:
|
Plz2 |
|
Pl2z |
|
Pl3 |
|
Pl3 |
|
|
z |
z2 |
|
|
|
Pl3 |
. |
||
|
|
|
|
|
||||||||||||||
v(z)= - |
|
+ |
|
|
- |
|
= - |
|
1 |
- 2 |
|
+ |
|
; vm ax = |
|
v(0)= |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2EJo |
|
EJo |
|
2EJo |
|
2EJo |
|
l |
l2 |
|
|
|
2EJo |
|
|||
Аналогичным образом нетрудно получить максимальный прогиб для консольной балки постоянного сечения (bo×h): vmax=Pl3/3EJo.

6.7.2. Метод единичной нагрузки. Интеграл Мора
Общие методы определения перемещений в упругих системах основаны на использовании вариационных принципов механики.
Наиболее часто применяется принцип возможных перемещений
(принцип Лагранжа): если упругая система находится в равновесии, то сумма работ всех внешних и внутренних сил на возможных бесконечно малых перемещениях равна нулю. В математической форме это можно записать так:
∑ Pjδ j + U== 0, |
(6.22) |
j |
|
где Pj - внешняя сила; δ j - возможное перемещение точки приложения силы Pj; U - возможная работа внутренних сил.
Под возможными понимаются такие перемещения, которые могут быть осуществлены для данной системы в соответствии с имеющимися опорами, не нарушая сплошности системы. Чем меньше перемещения, тем точнее соблюдается принцип Лагранжа. Учитывая
малость перемещений в реальных упругих системах, такие перемеще-
ния можно принимать в качестве возможных. Работа внешних и внутренних сил на возможных перемещениях называется возможной работой.
Пусть криволинейный брус испытывает плоскую деформацию под действием произвольной нагрузки, которую символически обозначим силой Р (рис. 6.17,а). Требуется определить перемещение се-
чения К в заданном i-ом направлении (δ (i)ê ).
Рассмотрим два состояния заданной системы. Исходное состояние системы при действии реальной нагрузки, в котором возникает искомое перемещение, называется действительным или грузовым состоянием. Вспомогательное состояние системы определяется действием соответствующей единичной нагрузки и называется еди-
ничным состоянием (рис.6.17,б). Термин «перемещение» понимается в обобщённом смысле: линейное или угловое перемещение. Вво-
димая единичная нагрузка должна соответствовать искомому перемещению: прикладывается в заданном сечении и в заданном направлении; прикладывается единичная сила (P = 1), если определяется линейное перемещение, или единичный момент (M = 1), если определяется угол поворота.
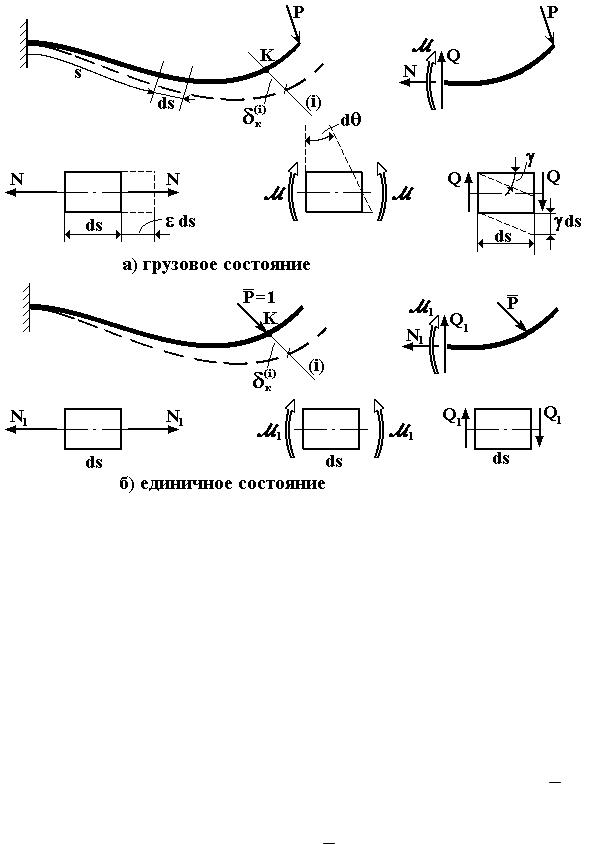
Рис. 6.17
В рассматриваемом методе принцип возможных перемещений записывается для единичного состояния. При действии единичной нагрузки в поперечных сечениях бруса возникают внутренние силовые факторы: нормальная сила N1, изгибающий момент M 1 и поперечная сила Q1. Возможные перемещения определяются дополнительным деформированным состоянием, которое накладывается на упругую систему, до того находившуюся в равновесии под действием приложенной нагрузки. В качестве возможных принимаются реальные перемещения бруса в грузовом состоянии, при котором в поперечных сечениях бруса возникают внутренние силовые факторы N, M , Q.
Для единичного состояния внешней силой является только P = 1, которая совершает работу на искомых перемещениях δ (Êi); поэтому
возможная работа внешних сил равна P δ (i)ê . При составлении работы внутренних сил рассматривается деформация элемента бруса длиной ds (см. рис. 6.17). Условно считая левое сечение неподвижным, правое сечение получит такие смещения: при растяжении (сжатии) - осе-
вое перемещение ε ds; при изгибе - поворот dθ =k ds; при сдвиге - поперечное перемещение γds (см. рис. 6.17,а). Работа dU внутренних сил для элемента бруса всегда отрицательная, т.к. эти силы являются силами упругого сопротивления и препятствуют развитию деформации. Поэтому получим:
dU = − N1 ε ds− M 1 kds− Q 1 γ ds.
Перемещения за счёт сдвига записаны при условии равномерного распределения касательных напряжений в сечении. Учитывая неравномерность их распределения при изгибе (см. раздел 6.4), вводится поправочный коэффициент kc - коэффициент формы сечения (для прямоугольного сечения kc = 6/5, для сплошного круглого сечения kc
= 10/9 и т.д.).
Для бруса в целом работа внутренних сил получается интегрированием выражения для dU по длине l. Подстановка полученных выражений в формулу (6.22) даёт уравнение:
l |
l |
l |
1 δ (i)K − ∫ N 1ε ds−− |
∫ M 1kds−− |
∫ Q 1kcγγ ds= 0. |
0 |
0 |
0 |
Откуда выражение для искомого перемещения получается в виде
l |
l |
l |
|
δ (i)K = ∫ N 1ε ds− |
∫ M 1kds− |
∫ Q 1kcγγ ds. |
(6.23) |
0 |
0 |
0 |
|
Подставляя в выражение (6.23) ранее полученные зависимости для деформаций ε , k, γ через внутренние силовые факторы (ε =N/EF,
k=M /EJx, γ =Q/GF), получаем расчётную формулу для определения перемещений:
δ |
|
|
|
l |
N 1 N ds |
|
l |
M |
1M ds |
+ |
l |
|
Q 1Q ds |
|
|
|
|||||||||
(Ki) = ∫ |
+ ∫ |
|
∫ |
|
kc |
. |
|
(6.24) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
0 |
|
E F |
0 |
|
|
|
E Jx |
0 |
|
|
|
|
G F |
|
|
||||||
Формула (6.24) носит название интеграла Мора. |
|
|
|||||||||||||||||||||||
В случае расчёта бруса, имеющего несколько участков, формула |
|||||||||||||||||||||||||
(6.24) может быть представлена в следующем виде: |
|
|
|||||||||||||||||||||||
(i) = |
m |
li |
N 1iN ids+ |
li |
M 1iM ids |
|
li |
k |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
Q 1iQ ids |
|
||||||||||||||
δ K |
|
∑ |
|
∫ |
|
|
|
|
|
∫ |
|
|
|
|
|
+ |
∫ |
ci |
|
|
, (6.25) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
i 1 |
0 |
|
E iFi |
|
|
0 |
|
E iJxi |
|
|
|
0 |
|
|
|
G iFi |
|
|
|||||
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где m - количество участков бруса.
Вклад каждого из интегралов в формулу (6.24) различный, что обычно учитывается при расчёте конкретного бруса. Для бруса при растяжении-сжатии учитывается только первый интеграл. При плос-

ком изгибе прямолинейного бруса обычно учитывается только второй интеграл:
δ |
l |
M 1M dz |
|
|
|
(Ki) = ∫ |
. |
(6.26) |
|||
|
|||||
|
0 |
E Jx |
|
||
Определение перемещений по методу единичной нагрузки проводится в следующем порядке.
1. Брус разбивается на участки в соответствии с действующей нагрузкой и характером изменения жесткости.
2.На каждом участке для грузового состояния составляются выражения для N, Q, M в произвольном сечении бруса.
3.Рассматривается единичное состояние бруса, определяемого действием соответствующей единичной нагрузки: в направлении искомого перемещения при определении линейного перемещения при-
кладывается сила P = 1, при определении углового перемещения момент M = 1.
4.На каждом участке бруса для единичного состояния составляются выражения для N1, M 1, Q1 в произвольном сечении бруса.
5.Вычисляется перемещение по формуле (6.24) (или (6.25),
(6.26).
Положительное значение показывает, что перемещение происходит по направлению приложенной единичной нагрузки, отрицательное - в направлении, противоположном приложенной единичной нагрузки.
6.7.3. Способ Верещагина
Использование формул (6.24) - (6.26) связано с необходимостью вычисления интегралов, иногда - путем численного интегрирования. Существуют различные способы, облегчающие вычисление этих ин-
тегралов. Один из них, графоаналитический способ А.К. Верещагина, применяется для прямолинейного бруса.
Рассмотрим прямолинейную балку постоянной жесткости (EJx=const), и формулу (6.26) представим в виде
δ |
= |
1 |
l |
|
|
∫ M 1M dz. |
(6.27) |
||||
EJx |
|||||
|
|
0 |
|
||
|
|
|
|
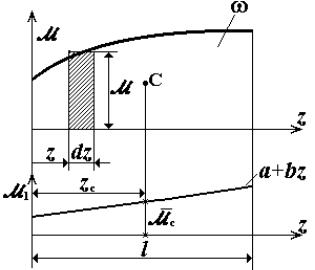
Для прямолинейной балки выражение для изгибающего момента M 1 от единичной нагрузки является линейной функцией:
|
|
|
|
|
|
|
|
|
M 1 = a + b z. |
(6.28) |
||||||
|
|
|
|
|
|
|
|
Выражение |
для изгибающего |
|||||||
|
|
|
|
|
|
|
|
момента |
M |
грузового состоя- |
||||||
|
|
|
|
|
|
|
|
ния может быть произвольной |
||||||||
|
|
|
|
|
|
|
|
функцией (рис. 6.18). После |
||||||||
|
|
|
|
|
|
|
|
подстановки |
выражения (6.28) |
|||||||
|
|
|
|
|
|
|
|
в формулу (6.27) в результате |
||||||||
|
|
|
|
|
|
|
|
преобразований получим: |
||||||||
|
|
|
|
|
|
|
|
δ = |
|
1 |
|
l |
|
|||
|
|
|
|
|
|
|
|
|
|
∫ (a+ bz)M dz= |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
EJx 0 |
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
l |
l |
||
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
∫ |
|||
|
|
|
|
Рис. 6.18 |
|
|
= |
|
|
(a M dz+ |
b zM dz). |
|||||
|
|
|
|
|
|
|
EJx |
0 |
0 |
|||||||
|
Введём обозначения (согласно геометрическому смыслу слагае- |
|||||||||||||||
мых): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
l |
|
∫ dω = ωω - площадь грузовой эпюры M |
(см. рис.6.18); |
|||||||||||||
∫ M dz = |
||||||||||||||||
0 |
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
||
l |
zM dz= |
|
|
zdω = z ω= |
S |
- |
статический момент площади эпюры |
|||||||||
∫ |
∫ |
|||||||||||||||
|
|
c |
|
M |
|
|
|
|
|
|
|
|
||||
0 |
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
||
M. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Тогда получим: |
|
|
ω (a+ bzc). |
|
|
|
|
|
|||||||
|
δ = |
|
1 |
(aωω++ bzcω )== |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
EJx |
|
|
EJx |
|
|
|
|
|
||||
Сомножитель в скобках согласно выражения (6.28) является значением момента M 1 в сечении z = zc (см. рис. 6.18). Обозначив η = M 1(zc) = a + bzc, формула для определения перемещений по способу Верещагина примет вид:
δ = ω η . |
(6.29) |
EJx |
|
Таким образом, вычисление перемещений по способу Верещаги- |
|
на сводится к перемножению площади (ω) грузовой эпюры M на ор- |
|
динату (η) единичной эпюры M 1 под центром площади грузовой |
|
эпюры. |
|
Следует обратить внимание, что эпюры M 1 и M |
для вычисления |
перемещений по формуле (6.29) должны удовлетворять определённым условиям:
1) грузовая эпюра M непрерывна и сохраняет знак на всем участке интегрирования;
2) площадь и положение центра площади грузовой эпюры M известны или легко определяются;
3) единичная эпюра M 1 является линейной (а не кусочнолинейной).
В том случае, если эпюры M и M 1 не удовлетворяют указанным условиям, грузовая эпюра разбивается на n простых фигур, чтобы удовлетворялись эти условия, и перемещение вычисляется по формуле:
δ = |
1 |
∑n ωω iη i. |
(6.30) |
|
|||
|
E Jx i= 1 |
|
|
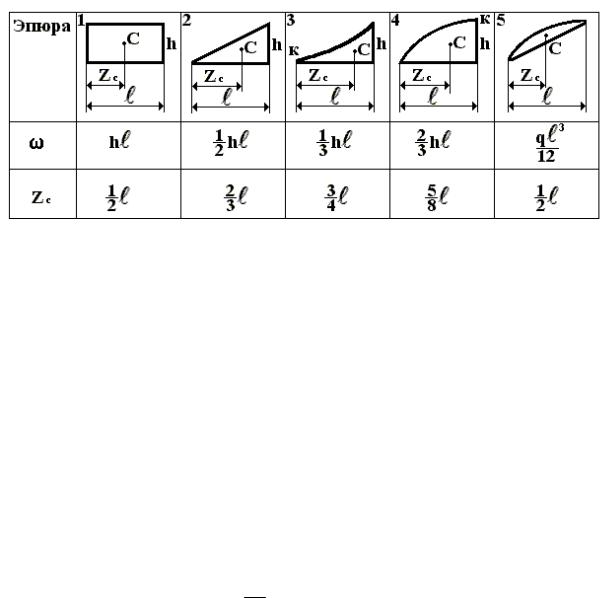
Вспомогательнаяинформациядлянекоторыхфигурприведена в табл. 6.1. Таблица 6.1
Фигуры 3 - 5 получаются для эпюры M , ограниченной квадратичной параболой (при действии распределенной нагрузки q = const),
причем для фигур 3, 4 (параболические треугольники) т.К должна быть точкой экстремума (min или max).
Способ Верещагина применим для вычисления любого из интегралов (6.24) с использованием соответствующих эпюр и жесткостей. Отметим ограничение и дополнительные особенности применения способа Верещагина (на примере формулы (6.29) для балки).
1. Способ Верещагина применим только для прямолинейного бруса.
2. Ступенчатый брус следует разбивать на участки постоянной жёсткости; тогда расчётная формула примет вид:
δ |
n |
ω η |
|
|
= ∑ |
i i |
. |
(6.31) |
|
|
||||
|
i= 1 |
E Jxi |
|
|
3. Для бруса переменной жесткости EJx(z) можно построить приведённую грузовую эпюру Ì = Ì /ÅJx; тогда формула (6.30) преобразуется к виду:
