Решение уравнений вида
Теорема (о корне).
Пусть функция f – возрастает (или убывает) на промежутке I, число а – любое из значений, принимаемых f на этом промежутке. Тогда уравнение f(x)=а имеет единственный корень в промежутке I.
Функция тангенс
возрастает на интервале
и принимает все значения из
.
Следовательно, по теореме о корне для
любого числа а, в интервале
существует единственный корень b
уравнения tgx=a.
Это число b называют
арктангенсом числа а и обозначают
arctg a.
О. Арктангенсом числа а называется такое число из интервала, , тангенс которого равен а.
При любом а
на интервале
имеется ровно одно число х, такое,
что tg x=a,
- это
.
Поэтому уравнение
tg x=a
имеет на интервале
длиной
единственный корень. Функция тангенс
имеет период .
Следовательно, все остальные корни
уравнения отличаются от найденного на
n
(
),
т.е.
.
Р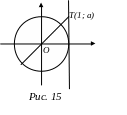
ешение
уравнения tg x=а
удобно проиллюстрировать с помощью
линии тангенсов (см. рис.15).
Для любого числа а на линии тангенсов
есть лишь одна точка с ординатой а
- это точка
.
Прямая ОТ пересекается с единичной
окружностью в двух точках; при этом
интервалу
соответствует точка
правой полуокружности, такая, что
.
Решение уравнений вида
Теорема (о корне).
Пусть функция f – возрастает (или убывает) на промежутке I, число а – любое из значений, принимаемых f на этом промежутке. Тогда уравнение f(x)=а имеет единственный корень в промежутке I.
Функция котангенс
убывает на интервале
и принимает все значения из
.
Следовательно, по теореме о корне, для
любого числа
а,
в интервале
существует единственный корень b
уравнения
.
Это число b называют
арктангенсом числа а и обозначают
arcсtg
a.
О. Арккотангенсом числа а называется такое число из интервала, , котангенс которого равен а.
При любом а
на интервале
имеется ровно одно число х, такое,
что
,
- это
.
П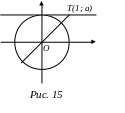
оэтому
уравнение
имеет на интервале
длиной
единственный корень. Функция тангенс
имеет период .
Следовательно, все остальные корни
уравнения отличаются от найденного на
,
т.е.
.
Решение уравнения
удобно проиллюстрировать с помощью
линии котангенсов (см. рис.15). Для любого
числа а на линии котангенсов есть
лишь одна точка с ординатой а - это
точка
.
Прямая ОТ пересекается с единичной
окружностью в двух точках; при этом
интервалу
соответствует точка
правой полуокружности, такая, что
.
Решение уравнений типа с помощью вспомогательного аргумента.
Рассмотрим
уравнение
,
где
.
Поделим обе части
уравнения на
,
т.к.
,
то
,
следовательно деление возможно.
Получим:
Рассмотрим сумму
квадратов:
,
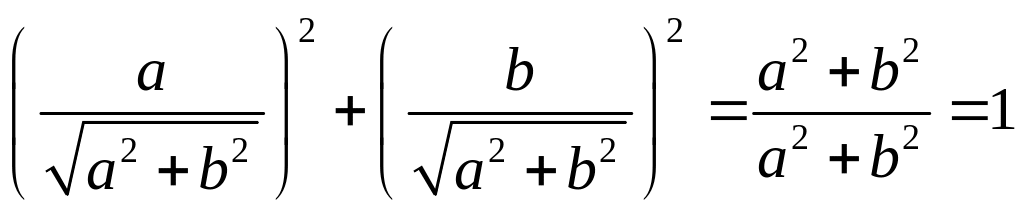Это означает, что
точка
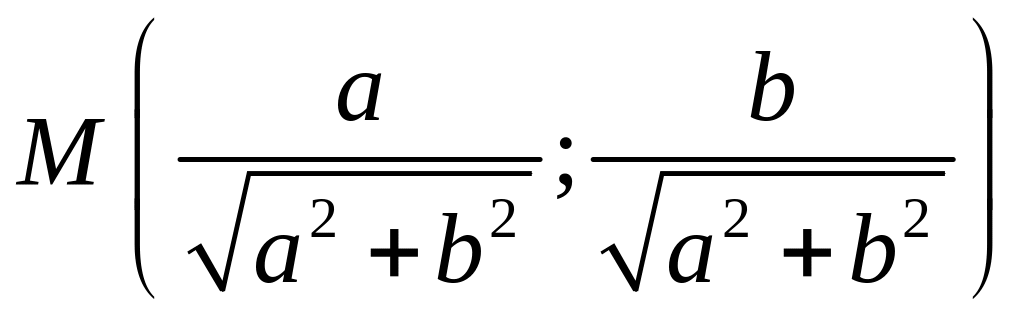лежит на единичной окружности, причем
координаты этой точки есть
и
или
и
для некоторых углов
и
.
Т.о., получим, что
,
а ,
,
причем,
.
Тогда, уравнение
принимает вид:
Тогда, если:
,
то уравнение
корней не имеет.
если:
,
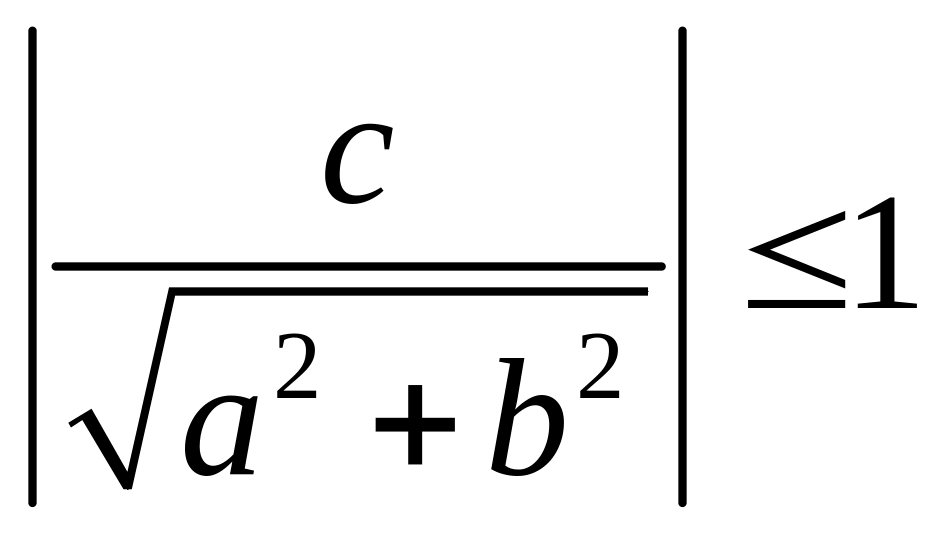то уравнение
имеет
корни:
,
отсюда
В случае
Тогда, если: , то уравнение корней не имеет.
если: , то уравнение имеет корни:
,
отсюда
