23. Тригонометрические функции двойного и половинного аргумента

Формулы сложения позволяют выразить , и через тригонометрические функции угла .

Рассмотрим формулы:

Положим в этих формулах равным . Получим:

Полученные формулы: называют формулами двойного угла.

Замечание. Воспользовавшись основным тригонометрическим тождеством, формулу косинуса двойного угла можно переписать в виде

.

Из формул двойного аргумента легко выводятся формулы половинного аргумента:

,

и

24. 

Рассмотрим тригонометрическую окружность. Повернем радиус , равный , около точки на угол и на угол . Получим радиусы и .

Найдем скалярное произведение векторов и

Пусть координаты точки равны , координаты точки равны . Эти же координаты имеют соответственно и векторы и .

По определению скалярного произведения векторов:

Выразим скалярное произведение и через тригонометрические функции углов и . Из определения косинуса и синуса следует, что

Подставив значения в правую часть равенства , получим

С другой стороны, по теореме о скалярном произведении векторов, имеем:

.

Угол BOC между векторами и может быть равен или , либо может отличаться от этих значений на целое число оборотов.

В любом из этих случаев, так как

Поэтому

Из равенств и следует:

,

Поделив обе части равенства на , получаем

С помощью формулы легко получить следующую формулу

Так как

Поделим числитель и знаменатель на , получим

Поделим числитель и знаменатель на , получим

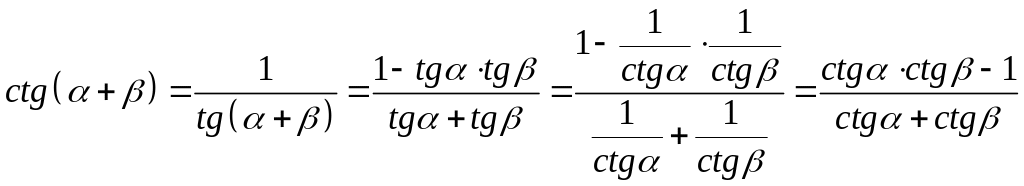
Аналогично для (проведите доказательство самостоятельно)

25. Преобразование суммы (разности) в произведение

Сумму и разность синусов или косинусов можно представить в виде произведения тригонометрических функций.

Чтобы представить в виде произведения сумму , положим и и воспользуемся формулами синуса суммы и синуса разности. Получим:

Решая систему , получаем, что и , таким образом.

Аналогично, можно вывести формулы разности синусов, суммы и разности косинусов.

26. Преобразование произведения в сумму.

Произведение ; ; можно представить в виде суммы тригонометрических функций.

Положим и ,

отсюда, решив систему: , получаем, и

Воспользуемся формулами преобразования суммы в произведение:

27. Обратные тригонометрические функции. (Теорема о корне и теорема об обратной функции)

Теорема о корне:

Пусть функция возрастает (убывает) на промежутке , число – любое из значений, принимаемых функцией на этом промежутке. Тогда уравнение имеет единственный корень в промежутке .

Теорема об обратной функции:

Если функция возрастает (убывает) на промежутке , то она обратима и обратная к ней функция , определённая на множестве значений функции , так же является возрастающей (убывающей).