2.4.3 Решение нелинейных узловых уравнений методом Ньютона.

Его основное преимущество — быстрая сходимость, однако он более трудоёмок на каждой итерации.

Для реализации решения узловых уравнений методом Ньютона, уравнения (39) представим в виде (для четырех узлов)

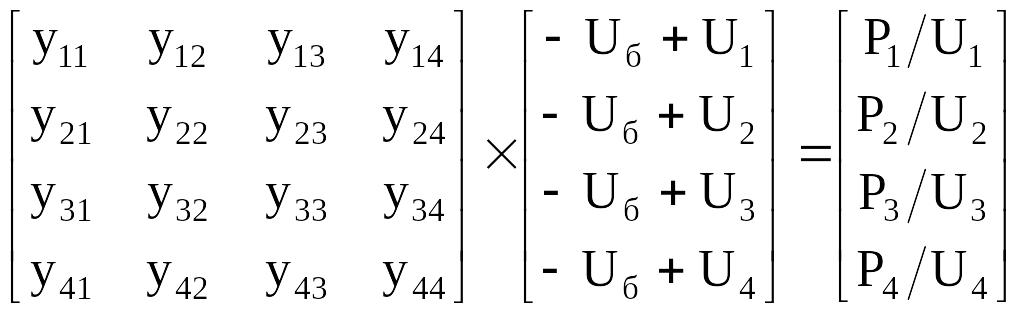 (146)

Перемножив, получим:

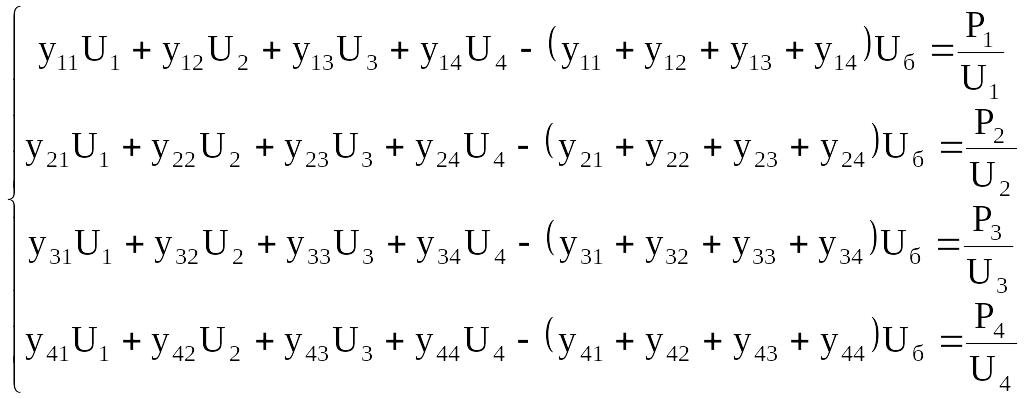(147)

Используем вектор-функцию W(U):

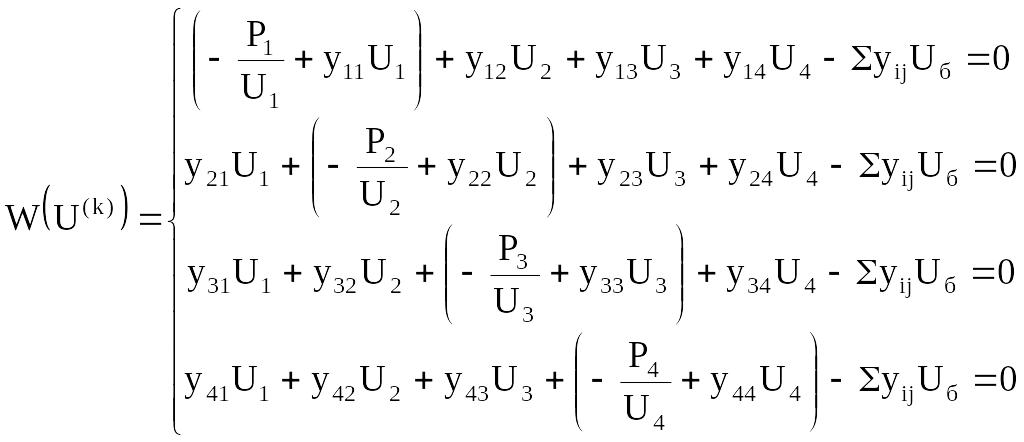(148)

Составляем матрицу Якоби:

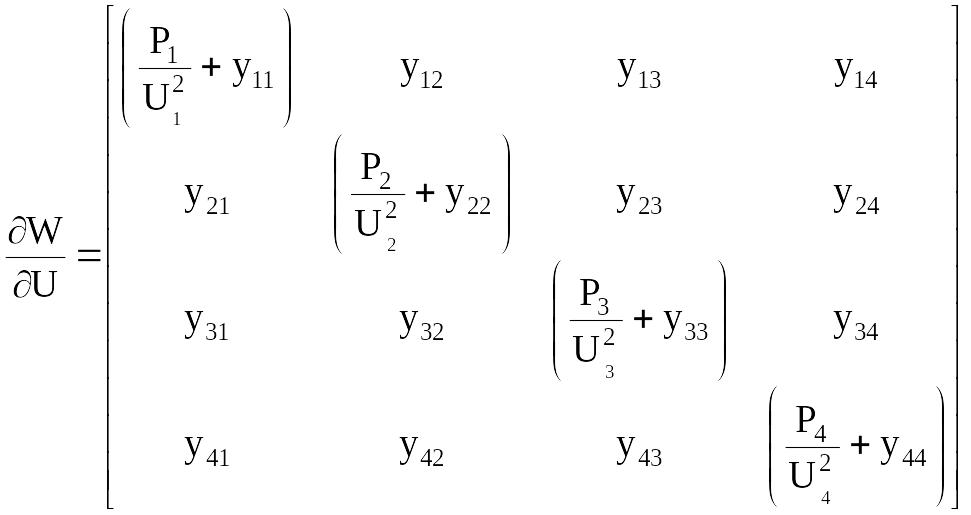, (149)

тогда итерационная формула запишется в виде:

, (150)

где

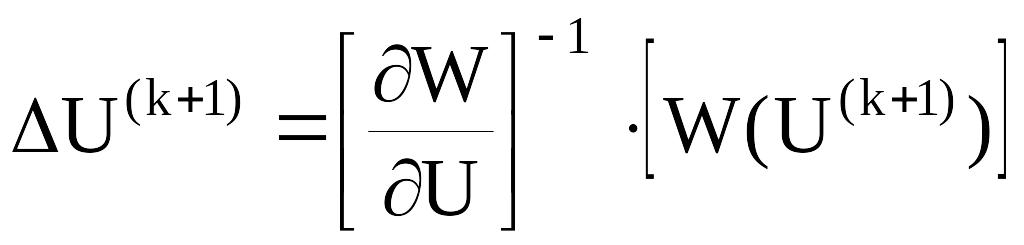. (151)

Точность проверяется следующим образом:

(152)

После определения узловых напряжений выполняется расчет режима электрической сети.

1. Определяются падения напряжение в узлах относительно напряжения в балансирующем узле:

, (153)

где

— напряжения в узлах;

n — единичная матрица-столбец.

2. Определяются токи ветвей:

, (154)

где

— диагональная матрица проводимостей ветвей;

— транспонированная матрица инциденций.

3. Определяются падения напряжения на ветвях схемы:

(155)

4. Определяются потоки мощности в ветвях:

, (156)

где — номинальное напряжение.

5. Определяются потери мощности в ветвях:

. (157)

6. Определяются суммарные потери мощности в сети:

. (158)

7. Определяются расчетные токи узлов:

. (159)

8. Определяются расчетные мощности в узлах:

, (160)

где — диагональная матрица напряжений в узлах.

9. Для каждого узла определяется небаланс по мощности:

, (161)

и в %:

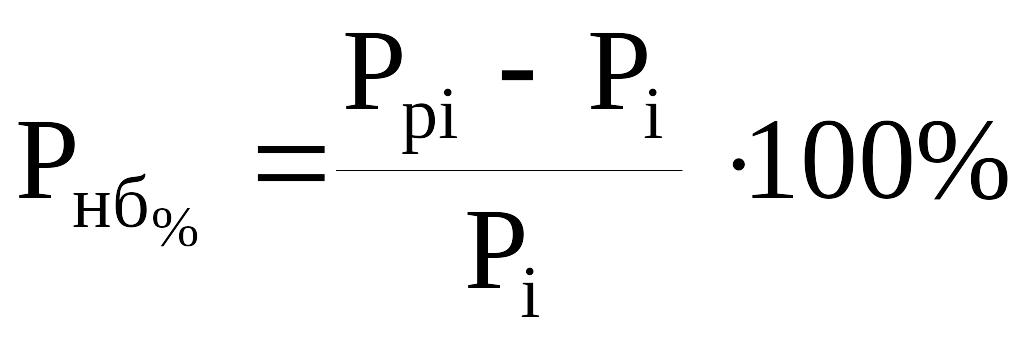, (162)

где

— рассчитанная мощность,

— заданная мощность.

Вопросы для самопроверки

1. В чем сходство и различие методов простой и ускоренной итерации?

2. Объясните принцип решения системы нелинейных уравнений узловых напряжений методом простой итерации.

3. Объясните принцип решения системы нелинейных уравнений узловых напряжений методом ускоренной итерации.

4. Объясните принцип решения системы нелинейных уравнений узловых напряжений методом Ньютона.

5. В чём отличие метода касательных от метода секущих при решении системы уравнений методом Ньютона?

6. Какой из рассмотренных в работе методов обеспечивает большую скорость сходимости итерационного процесса?

7. Что влияет на сходимость итерационного процесса?

III. Задание на курсовую работу

1. Тема работы: Применение матричных методов для анализа установившихся режимов электрических систем

2. Исходные данные к курсовой работе: Схема и параметры электрической сети, нагрузки узловых точек (определяются по методике, изложенной в Таблице 1)

Таблица 1. К определению исходных данных для вариантов задания

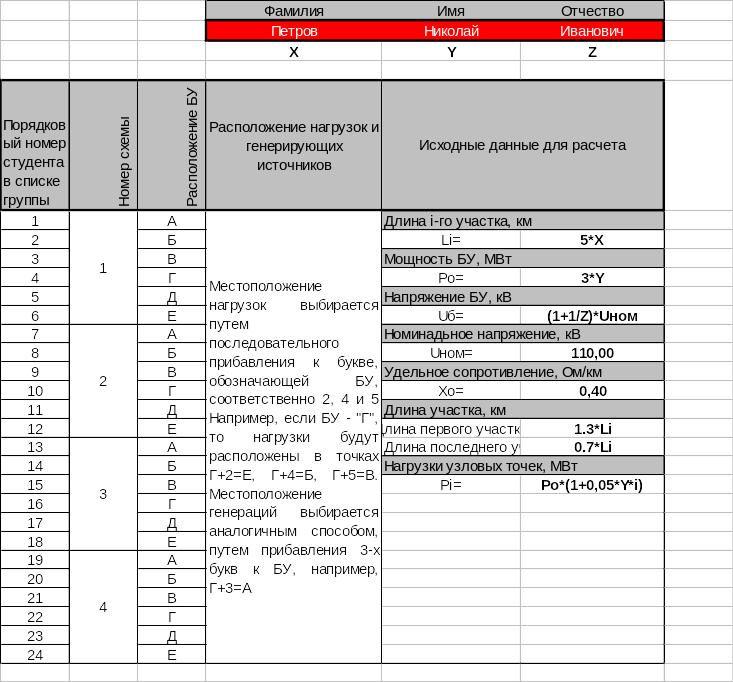
Схемы сети:

Д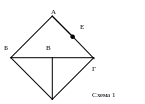

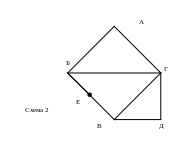
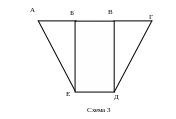
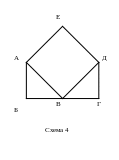
А

Б

В

Г

Е

Д

Схема 5

Пример определения параметров сети, согласно заданному варианту для Петрова Николая Ивановича, 21-го в списке группы (по методике, разработанной с участием студента Кабанова П.А.):

1. Схема сети рис.4

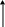
Балансирующий узел размещен в т. В

2. Нагрузки: В+2=Д Генерирующий источник: В+3=Е

В+4=A

В+5=Б

3. Базовая длина участка (Петров – 6 букв, Николай – 7 букв, Иванович – 8 букв):

Li = 5 · X = 5 · 6 = 30 км

Po = 3 · Y = 3 · 7 = 21 МВт

U_бу = (1 + 1/Z) U_ном = (1 + 1/8) 110 = 1,125 · 110 = 123,75 В

4. Согласно указаниям в Таблице 1, рассчитываем длины линий и нагрузки в узлах сети:

L₁ = 1,3 · 30 = 39 км

L_посл = 0,7 · 30 = 21 км

Нагрузки узловых точек:

Pi = Po (1 + 0,05 · Y · i)

P₁ = 21 (1 + 0,05 · 7 · 1) = 28,35 МВт

P₂ = 21 (1 + 0,05 · 7 · 2) = 35,7 МВт

P₃ = 21 (1 + 0,05 · 7 · 3) = 43,05 МВт

P₄ = 21 (1 + 0,05 · 7 · 4) = 50,4 МВт

P₅ = 21 (1 + 0,05 · 7 · 5) = 57,75 МВт

В результате получим вектор-столбец задающих мощностей в узлах сети:

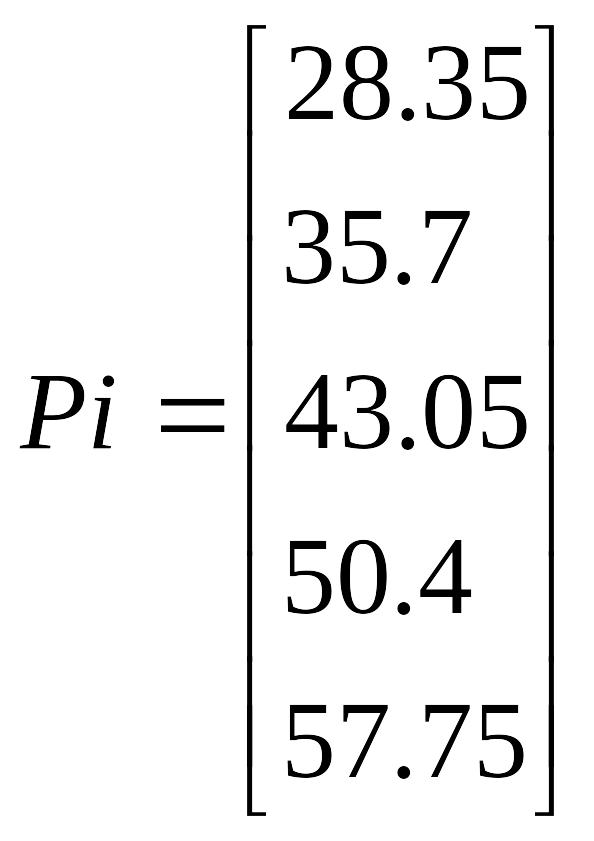
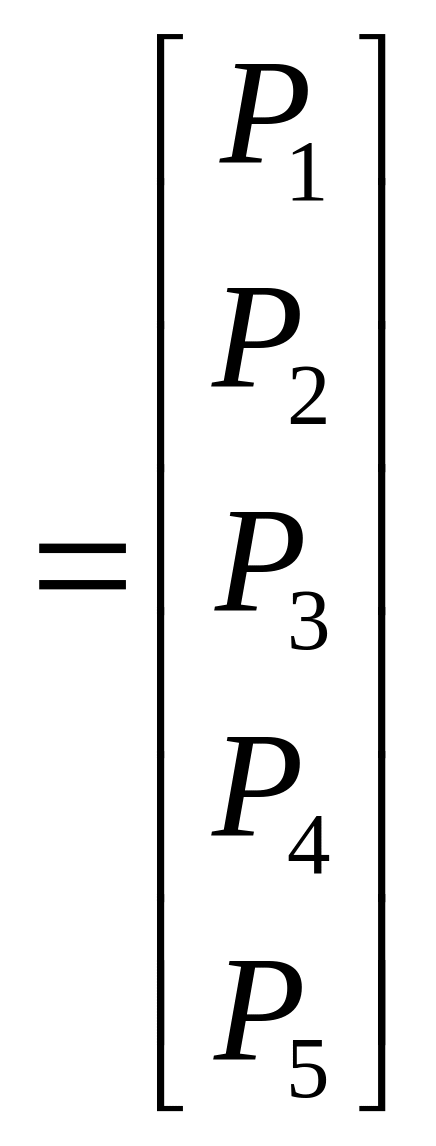
Заметим, что пока схема не пронумерована, нам не известно, какие номера получат узлы сети А-Е, какая нагрузка окажется в них приложена и какова мощность второго источника питания.

Эта методика определения исходных данных для расчета предназначена лишь для самостоятельного формирования случайным образом неповторяющихся сочетаний параметров схем и режимов.

В реальных условиях мощности нагрузки узлов сети и длины участков соответствуют объектам на местности и географической карте.