4. Картины скоростей и частот вращения

Кинематическое исследование спроектированного планетарного редуктора удобно производить графически. Представление о распре­делении скоростей точек его звеньев можно получить, построив кар­тину скоростей.

Вектор скорости точки А колеса 1 (рис. 5) изображается в виде отрезка

где масштабный коэффициент картины скоростей, мс^-1/мм;

; , C - угловая скорость 1-го колеса, /I/ об/мин - его частота вращения.

Определение скоростей точек радиальной прямой колеса оп­ределится наклонной прямой ОА', проходящей через точки О и А'. Прямая распределения скоростей точек блока сателлитов 2,2’пройдет через точки А' и P, где Р - мгновенный центр вращения блока. Отрезок ВВ' пропорционален скорости точки В - оси сателлитов. Прямая распределения скоростей водила В’O проходит через точку В’ и O, находящуюся на центральной оси враще­ния.

Рис. 5. Картины скоростей и частот вращения

Для получения наглядного представления о частотах вращения n (или угловых скоростях ω) звеньев редуктора строят карти­ну частот вращения. С этой целью, выбрав некоторую точку О’ за начало отсчета, по горизонтальной оси откладывают отрезок

пропорциональный известной величине частоты вращения n, (или ω₁); масштабный коэффициент картины частот вращения. Проведя из точки 1 прямую, параллель­ную закону распределения скоростей точек колеса 1 - ОА' до пе­ресечения с перпендикуляром к горизонтали в точке О', получат точку О”. Лучи, проведенные из О' параллельно наклонным прямым АР и OВ’, на пересечении с горизонтальной осью дают точки 2 и h; отрезки О'2 и О'h пропорциональны соответственно частотам вращения блока сателлитов 2, 2' и водила h:

Примечание. Отрезок О'2 отложен в сторону отрицательного направ­ления численной оси что означает, что блок сателлитов вращается в направлении, обратном направлению вращения колеса 1. Подобным образом строят картины скоростей и частот вращения для других типов планетарных редукторов. Так, на рис.6 они построены для редуктора сх.С при входном водиле h

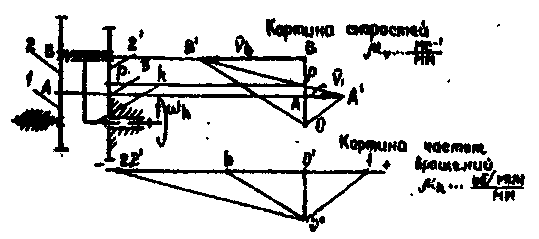
Рис.6. Картины скоростей и частот вращения для редуктора сх.С

1. Цель и задачи проектирования зубчатой передачи

Проектирование зубчатой передачи ставит целью определение ее размеров и качественных характеристик, зависящих от геометрии зацепления.

Правильно спроектированная передача позволяет добиться существенного повышения изгибной и контактной выносливости, уменьшения трения и изнашивания зубьев. При проектировании приходится решать и некоторые специальные задачи, например, вписывание в заданное межосевое расстояние.

Вычисленные в результате расчётов размеры передач нередко являются определяющими при проектировании различных узлов машины и существенно влияют на её габариты, а надежность и долговечность работы напрямую зависит от качества спроектированной передачи. Это тем более важно, что зубчатые механизмы являются наиболее распространенным видом механических передач и устанавливаются в большинстве современных машин.

Рис. 1. Схема механизмов машины:

I – двигатель, II – редуктор, III – рычажный механизм;

1, 2, 2′, 3 – Зубчатые колёса

2. Исходные данные и их анализ

Зубчатые механизмы в большинстве машин представленных в заданиях на курсовой проект, устанавливается между двигателем и рычажным механизмом (рис.1) и предназначены для передачи вращения от ротора двигателя к входному валу этого механизма со значениями частот вращения в пределах требуемого передаточного отношения:

где - частота вращения ротора двигателя, об/мин;

- частота вращения входного звена рычажного механизма, об/мин.

При заданной общей кинематической схеме зубчатых механизмов, куда входят рядовые зубчатые передачи, планетарные редукторы т.п. необходимо произвести разбивку общего передаточного отношения на частные значения, произведение которых равно этому общему

,

где - передаточное отношение зубчатого редуктора (обычно планетарного);

, - передаточные отношения рядовых зубчатых передач.

В одних заданиях на курсовой проект числа зубьев проектируемой зубчатой пары заданы, например и , в других же их предстоит определить через известное передаточное отношение , межосевое расстояние a_w и модуль m.

В этом случае с округлением до ближайшего целого числа, , которое также округляется.

Если задано суммарное число зубьев , то

.

Примечание. Нужно проверить, чтобы после округления и было выдержано условие

.

В некоторых случаях числа зубьев колёс могут быть не заданы, как не задано межосевое расстояние и передаточное отношение. В этом случае рекомендуется выбрать в интервале 11…15, а , где должно быть , в редких случаях до 6.

Помимо чисел зубьев и модуля заданными являются параметры инструментов реечного типа – гребёнки: - угол профиля зуба инструмента; - коэффициент высоты головки зуба инструмента; - коэффициент радиального зазора инструмента.