3. Синтез планетарных зубчатых редукторов

При синтезе нужно выбрать схему механизма. Предпочтительней те редукторы, которые позволяют получить высокий к.п.д., малые габариты и вес. После этого производят определение чисел зубьев колес, так чтобы обеспечить заданное передаточное отношение , условия соосности, соседства, равных углов между сателлитами (ус­ловие сборки) и правильного зацепления.

Обеспечение заданного передаточ­ного отношения (1-е условие); с целью упрощения под­бора чисел зубьев колес допускается, где это возможно, отклоне­ние U до 5 %.

Условие соосности (2-е условие) предполага­ет, что при расположении осей колес I, 3 и водила h на одной прямой (рис. За,б), должно быть обеспечено зацепление са­теллитов с центральными колесами. Для этого необходимо:

1. В сх. А выдержать равенство

r₁+r₂ =r₃-r₂=r_h ( 3 )

и учитывая, что колеса нулевые, их радиусы:

где m - модуль зацепления, мм; - число зубьев i-го колеса; условие соосности (3) можно записать в виде

или (5)

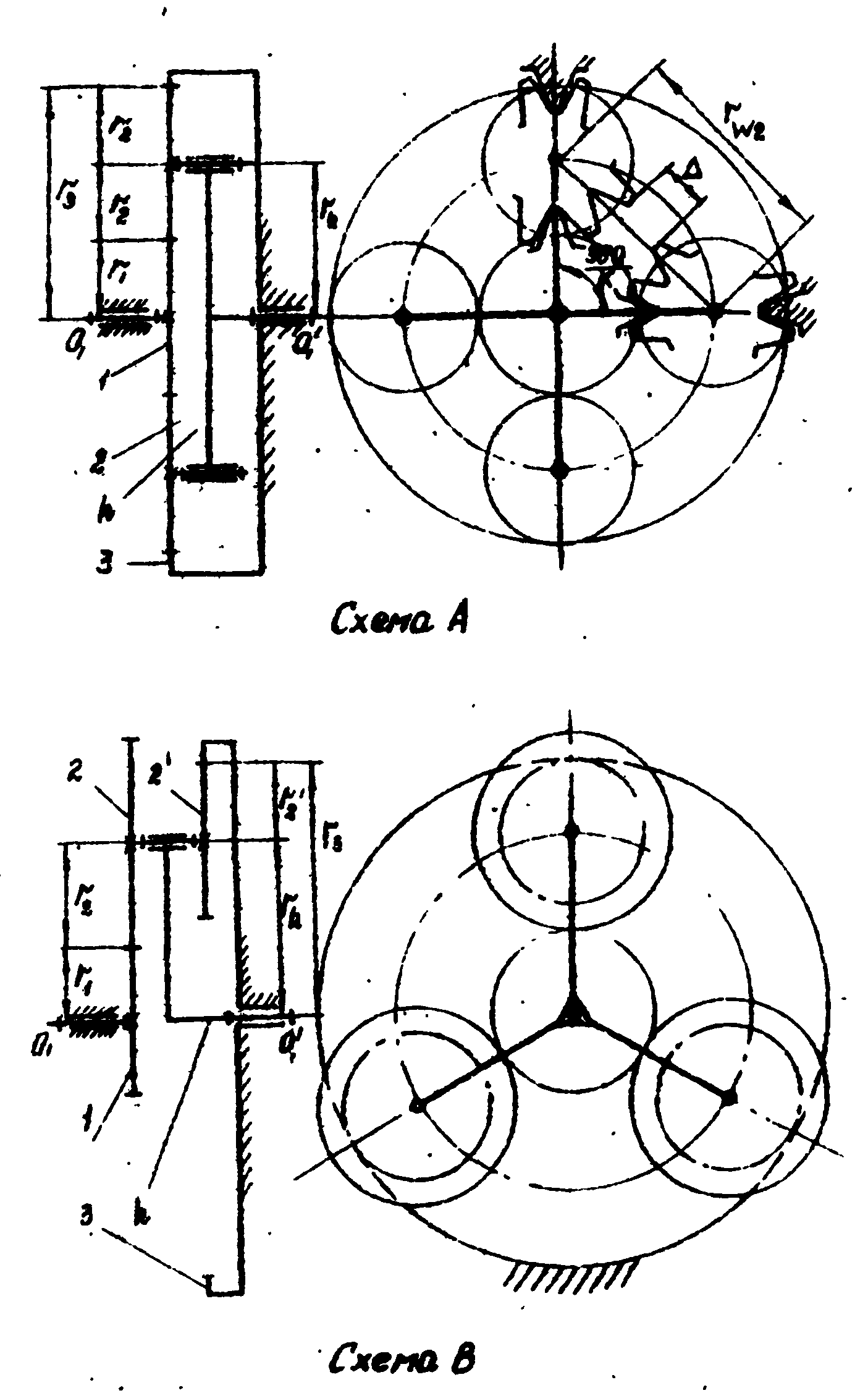
Рис. За. Схема планетарных редукторов А и В

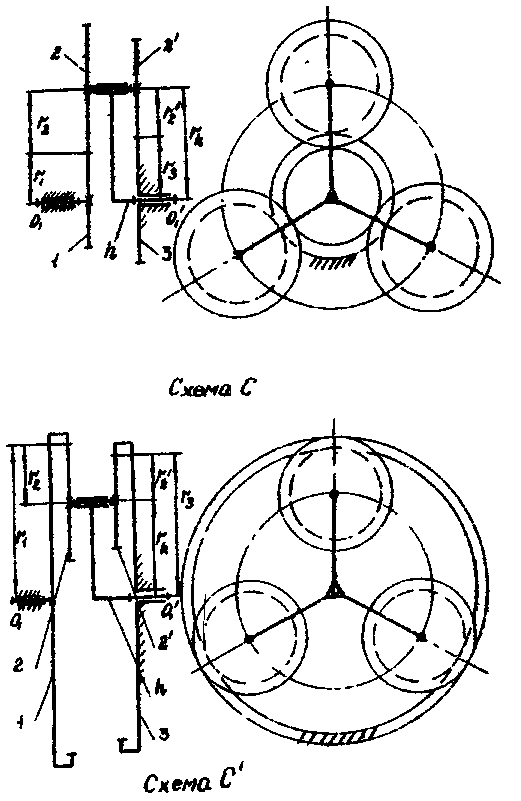
Риг. 3б. Схемы планетарных редукторов С и С′

2. В сх.В (6)

3. В сх.С (7)

4. В сх.С’ (8)

Примечание. В случае, если в сх.В, С и С’ модули ступеней пере­дачи 1, 2 и 2', 3 разные (соответственно и ), нужно ввести сомножитель , и тогда для сх. В, напри­мер, условие (6) примет вид

(6’)

Условие соседства (3-е условие) требует, чтобы соседние сателлиты не задевали своими зубьями друг друга, для чего должно бить обеспечено неравенство (рис. 3, а)

,

где - радиус окружности вершин зубьев сателлита. Расчетные Формулы для сх.А, В, С имеют вид

(9)

и для сх.С’

(10)

Здесь К - число сателлитов (блоков сателлитов); обычно заданы в исходных данных, но могут быть и выбраны в зависимости от ; - стандартное значение коэффициента высоты головки зуба инструмента, которым нарезано данное колесо.

Условие равных углов между (1-е условие) сателлитами (условие сборки) учитывает необходи­мость одновременного зацепления всех сателлитов с центральными колесами при симметричном расположении сателлитов. Расчетная формула

(11)

где Р = О, I, 2, 3, 4, ... ; С любое целое число.

Примечание. Вывод формулы [2 , стр. 423].

Условие правильного зацепления (5-е усло­вие): чтобы избежать заклинивания передач внутреннего зацепления, необходимо выбирать каждого колеса больше допустимого .

При ;

при ,

где - коэффициент высоты головки зуба инструмента, которым нарезается колесо с внутренними зубьями; - минималь­ное число зубьев того колеса с внешними зубьями, которое входит в зацепление с колесом, имеющим .

Кроме того нужно, чтобы при и при , .

Задача подбора чисел зубьев сводится к совместному решению рассмотренных условий. Методов решения существует несколько:

1) с помощью генерального уравнения,

2) метод сомножителей,

3) метод О.Н.Левитской, и другие.

1. Метод генерального уравнения [3 , стр.32-35] состоит в решении общего уравнения, которое включает условия 1, 2, 4, 5 с последующей проверкой условия 3 по формуле (9), Метод может быть рекомендован для редуктора сх.А (рис. 3).

Общее уравнение

, (12)

где С - любое целое число.

Пример. Дано: m = 2 мм, K = 4, = 4.

Решение ,

Выбираем, возможно, меньшее число зубьев . - 20.

Равенство можно переписать так

.

Получаем. = = 20, = 60, С = 20 - целое число.

Примечание. Если выбрать < 20, то не обеспечивается условие (5).

Уточнение действительного передаточного отношения редуктора

Отклонение от теоретического значения,

Проверка условия соседства (9)

0,707 > 0,55, условие выполняется.

2. Метод сомножителей [2 , стр. 425-42].

Подбор чисел зубьев Z ведется по условиям 1, 2, 5, про­верка по условиям 3, 4. Метод может быть рекомендован для сх. В, С, C' .

Рассмотрим на примере схемы С (рис. 36).Передаточное отношение для неё выражается по одной из формул (2), откуда получаем

заменяется отношением сомножителей a, b, c, d, каждый из которых должен быть пропорционален соответствую­щему Z

Учитывая эту пропорциональность и введя сомножители и , уравнение соосности (7):

можно переписать так

(14)

Сравнивая (7) и (14), получим:

где - общий сомножитель - любое число.

Рассмотрим числовой пример. Дано: m = 2 мм, K = 3, = 5;

Представим в виде отношения сомножителей

тогда

Учитывая, что Z должны быть по возможности меньшими числами, примем = 5, и получим = 20, = 40, = 15,

Действительное передаточное отношение

Отклонение = 0.

Проверка условия соседстве по формуле (9)

0,866>0.7. Условие выполняется.

Условие сборки проверяем по формуле (2)

При этом получается трансцендентное число, значит, условие не выпол­няется. В таком случае нужно пересчитать числа зубьев, подбирая другие сомножители a, b, c, d. Но можно оставить и этот вариант, если оговорить, что один из блоков сателлитов при сборке следует установить со смешением на некоторый центральный угол от­носительно его симметричного положения. Расчет этого угла в курсовых проектах не предусмотрен.

В схеме С (и С') входным звеном нередко выбрано водило h. В этом случае исходным является . Для того, чтобы воспользоваться приведенными расчетами, нужно перейти сначала к

(16)

При расчете методом сомножителей схемы В нужно иметь ввиду отличия к сравнению со сх.С:

а) условие соосности и

(17)

б)

Для схемы С’:

а) условие соосности

и (18)

б) условие соседства - формуле (10).

3. Метод О.Н.Левитской [4, стр.11З-115].

При синтезе по этому методу выполняется условие, при котором размер опорного колеса будет минимальным при заданном значении и одинаковом модуле всех колес. Метод рекомендуется при расчете сх.В (рис. 3а).

Нужно принять = 18...20 и более, по мере необходи­мости.

По формуле

(19)

определяется , из уравнения соосности

Пример. Дано: т = 2 мм, = 9, K = 3.

Принимаем = 18; по формуле (19)

Действительное передаточное отношение

Проверка условия соседства по формуле (9)

0,866 > 0,704. Условие выполняется. Проверка условия сборки по формуле (11)

- целое число; р = 0. Условие выполняется.

После определения Z колес редуктора подсчитывают началь­ные радиусы колес по формуле (4) и вычерчивают в выбранном масш­табе две проекции его схемы.