4. Достатні ознаки збіжності числових рядів.

4.1 Порівняльна ознака.

Розглянемо два ряди з невід'ємними членами (1), та

(2)

Теорема 2 (Порівняльна ознака) Якщо при будь-якому , то із збіжності ряду (2) випливає збіжність ряду (1), а з розбіжності ряду (1) випливає розбіжність ряду (2).

Наслідок. Якщо ж ряд (1) розбіжний , то і ряд (2) також розбіжний.

Приклад.

Дослідити збіжність ряду .

Розглянемо ряд . Для будь-якого . Із розбіжності ряду з меншими членами випливає розбіжність ряду з більшими членами, тому ряд є розбіжним.

4.2 Ознака д'Aламбера

Теорема 3 (Ознака д'Aламбера) Якщо для ряду (1) існує границя

то при <1 -- ряд збігається, при >1 -- ряд розбігається, при =1 -- ознака відповіді не дає.

4.3 Радикальна ознака Коші.

Теорема 4 (Радикальна ознака Коші) Якщо для ряду (1) існує границя

то при <1 ряд збігається, при >1 ряд розбігається, при =1 ознака не дає відповіді на поставлене питання

5. Степеневі ряди.

ОЗ 3 Степеневим рядом називається функціональний ряд:

(3)

де – сталі, які називаються коефіцієнтами ряду. Степеневий ряд позначається символом:

(4)

Теорема 5 (Теорема Абеля) Якщо степеневий ряд (4) збігається при деякому значенні то він абсолютно збігається при будь-якому значенні , для якого .

ОЗ 4 Ряд з довільними членами

(5)

називається абсолютно збіжним, якщо збігається ряд, складений із абсолютних величини його членів:

(6)

Якщо ж ряд (5) збігається , а ряд (6) розбігається, то ряд (5) називається умовно збіжним.

Наслідок. Якщо ряд розбіжний при деякому значенні , то він розбіжний при всякому , для якого .

З теореми Абеля випливає, що є три можливості для збіжності степеневого ряду:

1. Степеневий ряд збігається лише в одній точці ;

2. Ряд збігається в інтервалі симетричному відносно точки ;

3. Ряд збігається на всій числовій осі.

6. Область збіжності степеневого ряду.

ОЗ 5 Інтервалом збіжності степеневого ряду називається інтервал , такий що для всякої точки , що лежить всередині цього інтервалу, ряд збігається, а для будь-якого , що не належить інтервалу, ряд розбігається. Число називається радіусом збіжності степеневого ряду.

В точках збіжність ряду встановлюється в кожному випадку окремо.

Як знайти радіус збіжності степеневого ряду:

Розглянемо ряд (3). Припустимо, що існує границя:

За ознакою Даламбера ряд збігається, якщо , тобто і розбігається, якщо .

Із означення інтервалу збіжності випливає, що:

Користуючись ознакою Коші, можна одержати ще одну формулу для находження радіуса збіжності:

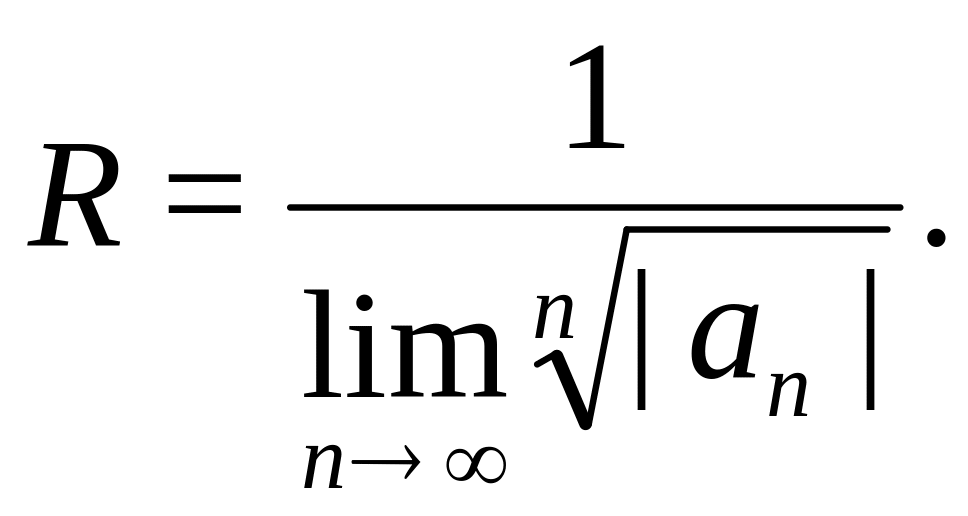
Степеневий ряд

(7)

можна отримати з ряду (3) за допомогою заміни .

7. Розклад деяких функцій в ряд Тейлора.

Нехай функція нескінченно диференційована в деякому околі точки , тоді ряд

(8)

має назву ряда Тейлора функції у точці , а при -- ряд Маклорена.

Розкладемо в ряд Маклорена елементарні функції.

Приклад. Розкласти в ряд Маклорена ф. .

Приклад. Розкласти в ряд Маклорена ф. .