2. Уравнения неразрывности, движения, энергии

2.1. Градиент скорости и связанные с ним кинематические тензоры

Градиент скорости является тензором второго ранга, который характеризует поле скоростей. В декартовом базисе его можно записать в виде:

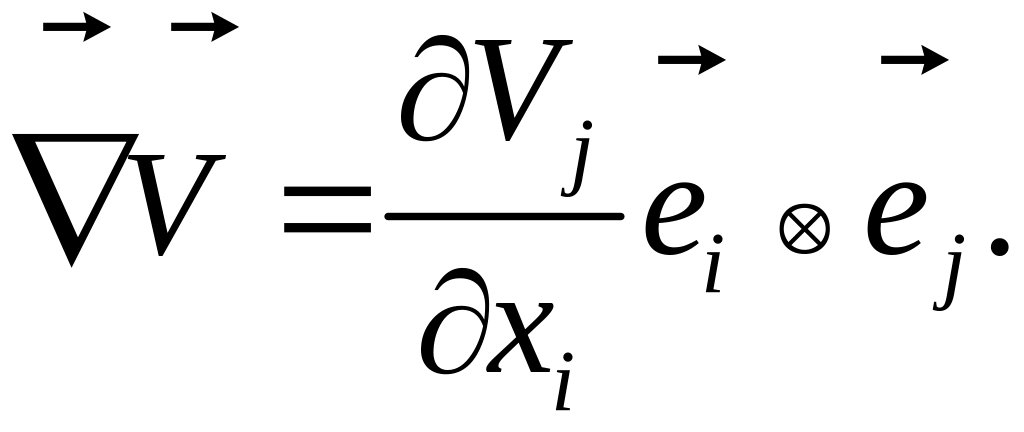
Т ранспонирование дает

Геометрический смысл тензора - это оператор, переводящий вектор в вектор :

Действительно:

Однако скалярное произведение не является дифференциалом . Действительно:

При этом нетрудно убедиться, что произведение в свою очередь является дифференциалом , так как произведение вектора на тензор второго ранга подчиняется правилу: отсюда

Иногда в литературе вместо оператора Гамильтона (набла) используют частную производную по радиус-вектору:

Тогда градиент скалярной функции записывают как , градиент вектор-функции (тензор второго ранга) как и т.д.

Симметричная часть есть тензор скоростей деформаций , а антисимметричная – тензор вращения :

Очевидно, что

В компонентном виде:

Здесь и далее, если не оговорено особо, следует читать как .

Скалярные произведения этих тензоров:

этот тензор является симметричным, как и этот:

Также симметричным является тензор

характеризующий вращательную часть производной Яуманна для тензора скоростей деформаций .

Заметим, что:

2.2. Операции с тензорами градиента скорости, скоростей деформации и тензора вращения, и их инварианты

Запишем в компонентном виде, в декартовом базисе скалярные произведения для градиентов скоростей:

Второй и третий из этих тензоров являются симметричными, а первый и четвертый – несимметричными. Соответствующие скалярные величины – двойные скалярные произведения:

Видно, что:

Для следов скалярных произведений:

откуда следует, что:

Инварианты тензоров

1) Для тензора градиентов скоростей:

его квадрат:

и его куб:

Соответствующие следы:

Тогда инварианты этого тензора:

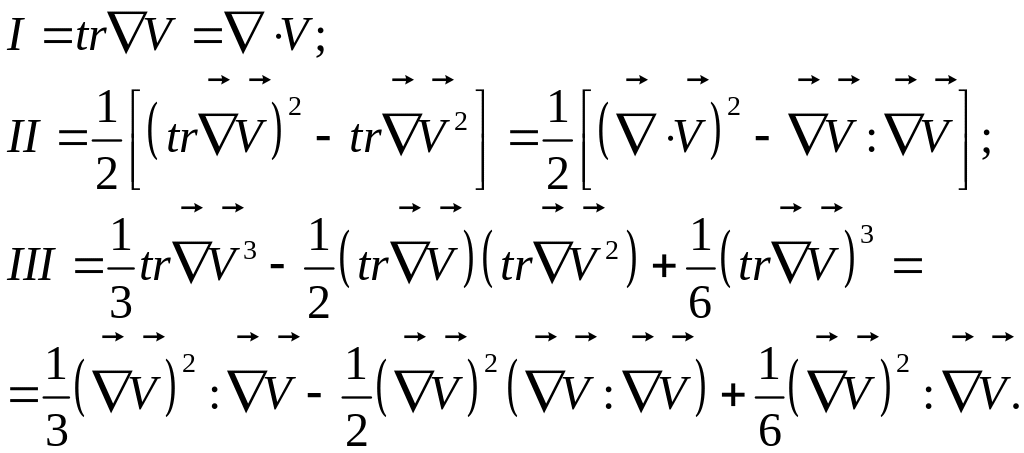
2) Для транспонированного тензора:

его квадрат и куб записываются так:

Их следы:

Тогда соответствующие инварианты:

3) Для тензора скоростей деформаций:

Квадрат и куб записываются как:

Их следы:

Инварианты тензора по найденным следам вычисляются по формулам:

2.2 Дифференциальные операторы для поля скоростей

Хорошо известно, что при использовании Эйлерового подхода к описанию движения жидкости появляется дополнительная компонента ускорения, обусловленная изменением пространственной конфигурации течения.

Конвективное ускорение можно записать в виде:

Как известно:

Этот вектор можно записать и по-другому, учитывая что

Отсюда следует еще одна формула для

Еще одно полезное соотношение:

Для поля скоростей кроме скалярного дифференциального оператора первого порядка , который дает конвективную производную, можно использовать и векторный дифференциальный оператор .

В компонентном виде его можно представить:

или, подробнее, в обычной форме записи для декартовой прямоугольной системы координат, это вектор с компонентами:

по осям , и , соответственно.

В предыдущем выражении для записи векторного произведения используется тензор Леви-Чевита (альтернирующий тензор):

Для скалярной функции величина является вектором:

Оператор , примененный к вектору, дает тензор второго ранга. Для поля скоростей имеем:

Матрица компонент этого тензора имеет вид:

Видно, что след этого несимметричного тензора:

где

Тот же самый результат дают скалярные функции:

Действительно:

Тензорным дифференциальным оператором второго порядка является оператор т.е. . В компонентном виде:

Матрица компонент этого симметричного тензора имеет вид:

Оператор Лапласа – скалярный дифференциальный оператор второго порядка есть след этого тензора:

Для двух векторов и их скалярное и векторное произведения могут быть записаны в тензорном виде через диады В компонентном виде тензор

матрица компонент этого несимметричного тензора имеет вид:

Видно, что след этого тензора есть скалярное произведение векторов:

Действительно:

Векторное произведение двух векторов и можно представить в виде:

т.е. в виде:

Действительно, левая часть этого равенства:

а правая:

Проекция этого вектора на ось имеет вид:

т.е. совпадает с проекцией на эту ось. Аналогичным образом можно увидеть совпадение и других двух проекций. Тем самым следует, что векторное произведение двух векторов есть двойное скалярное произведение антисимметричной части соответствующей диады, взятой с обратным знаком, и тензора Леви-Чивита.

Нетрудно убедиться в справедливости и такого равенства для векторного произведения векторов:

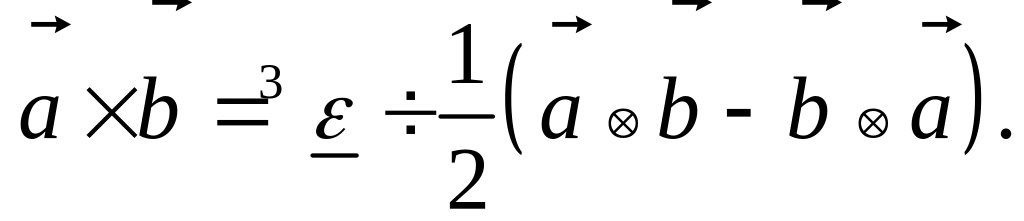
Для скалярных произведений вектора и тензора справедливы соотношения:

что следует из определения для операции транспонирования.

Очевидно:

Таким образом перестановка местами в скалярном произведении вектора и тензора приводит к появлению у тензора символа транспонирования.

Рассмотрим градиент скалярного произведения двух векторных функций и :

Тем самым получим формулу:

Применяя ее к величине , присутствующей во многих соотношениях гидродинамики, получаем:

Оператор конвективной производной, применимый к скалярным и векторным функциям, позволяет переходить к дивергентной форме записи:

Скалярное произведение:

дает антисимметричный тензор второго ранга. В компонентном виде это:

Матрица компонент этого тензора:

Тот же самый результат, но с обратным знаком, дает векторное произведение:

Таким образом:

Другие полезные формулы :

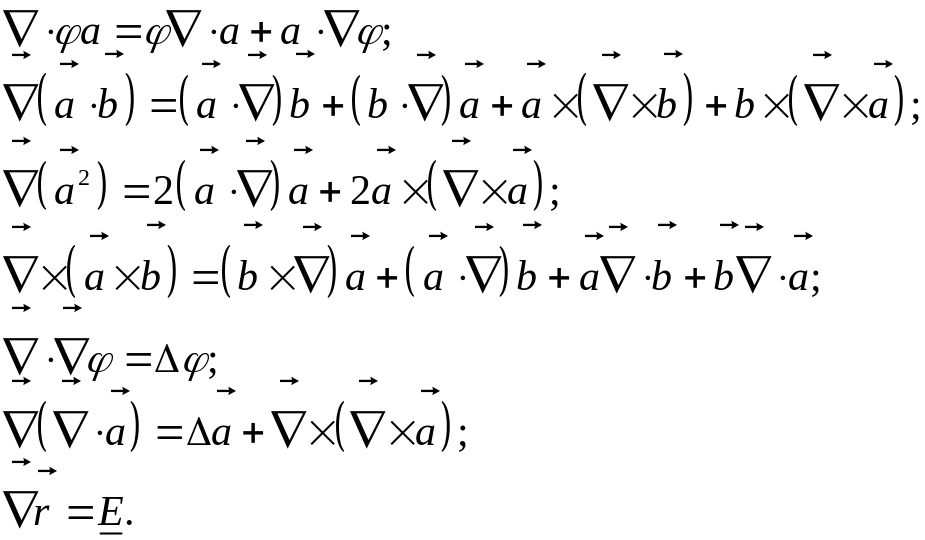
Двойное векторное произведение векторов есть разность двух векторов:

Для смешанного произведения векторов справедлива циклическая перестановка:

Единственный тензор и другие тензоры второго ранга, содержащие в матрице компонент единицы.

Как известно, единичный тензор (тензорная единица) – тензор второго ранга, который в декартовом прямоугольном базисе содержит в матрице компонент единицы, расположенные по главной диагонали:

где дельта Кронекера:

Матрица компонент имеет вид:

Этот тензор играет важную роль в тензорной алгебре – с его помощью вычисляют след тензора второго ранга, скалярное умножение тензора любого ранга на не меняет исходный тензор. Тензорная поверхность единичного тензора представляет собой сферу единичного радиуса. Любой шаровой тензор, характеризующий ту или иную физическую величину, записывается через тензор . Так, тензор напряжений идеальной жидкости представляют в виде:

где давлении. Это выражение можно трактовать как закон Паскаля в тензорном виде.

При записи физических соотношений иногда желательно иметь такой тензор второго ранга, у которого была лишь одна ненулевая компонента, расположенная к тому же не только на диагонали. Это нетрудно получить, используя дельты Кронекера. Например, тензор имеет матрицу:

Тензор характеризуется матрицей:

и т.д. При этом возможны различные комбинации. Например, тензор имеет матрицу компонент: