2.11. О вязкостях и

Для течения вязкой жидкости тензор напряжений Коши , который всегда симметричен по определению, обычно представляют в виде:

(1)

где - давление; - тензор вязких напряжений. Этот тензор равен нулю для идеальной жидкости, в отличие от жидкости, обладающей вязкостью. При этом, в ламинарном режиме является тензором чисто вязких напряжений, а при турбулентном течении он включает в себя, помимо вязких, еще и турбулентные напряжения.

В случае течения вязкой жидкости тензор напряжений линейно связан с тензором скоростей деформаций :

где двоеточие – символ двойного скалярного произведения; тензор - тензор материальных констант. Этот тензор четвертого ранга, имеющий 81 компоненту, переводит тензор в тензор . Для изотропной жидкости, число материальных констант становится равным не 81, а уменьшается до двух []. Эти две постоянные и называются постоянными Ламе и имеют смысл вязкостей, , при чем носит наименование динамической вязкости. В этом случае, соотношение (2) принимает вид:

(3)

где - след тензора (сумма его диагональных компонент в матрице компонент), который, как известно, определяется формулой:

(4)

т.е. имеет смысл дивергенции поля скоростей жидкости.

С учетом выражений (3) и (4), тензор напряжений в движущейся вязкой жидкости записывается в виде:

(5)

Величина характеризует скорость объемного расширения (сжатия) жидкости, ее физический смысл виден из формулы:

где - рассматриваемый объем жидкости.

Возьмем след тензорного равенства (5). Для левой части:

Величина , равная сумме диагональных компонент , равна следу правой части выражения (5), т.е. можно записать:

(6)

Отсюда, скорость объемного расширения (сжатия):

(7)

В равновесии, когда а так же при достижении покоя в жидкости, величина . Если же равновесия покоя нет, то .

Если в рассматриваемой точке внезапно возникнет давление , не равное давлению окружающей среды, , то величина будет равной и возникнет движение жидкости, скорость ее объемного расширения будет:

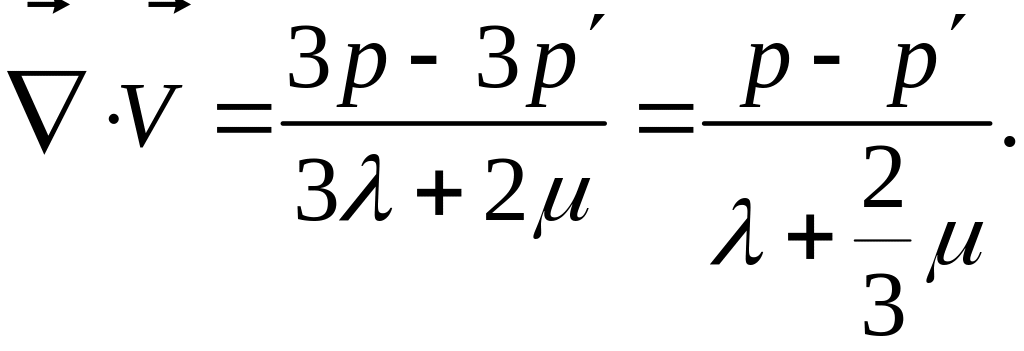
Величину называют объемной (второй) вязкостью и обозначают как :

(8)

Тогда предыдущая формула перепишется в виде:

Отсюда видно, что если , то величина и наоборот.

После истечения некоторого времени возмущение рассасывается, исчезает, давление , жидкость возвращается в исходное состояние, .

В гидродинамике называют жидкость стоксовой ньютоновской, если объемная вязкость

(9)

В этом случае , т.е. скорость изменения объема является бесконечно большой, возмущение распространяется бесконечно быстро. Модель стоксовой ньютоновской жидкости является наиболее используемой в современной гидродинамике вязкой жидкости [], для нее, согласно (8) и (9), имеем:

(10)

При этом выражение (6) дает:

Реологическим соотношением тогда будет, согласно формуле (5), следующее выражение:

(11)

или

(12)

После подстановки соотношения (11) в уравнение движения сплошной среды в напряжениях:

имеем векторное уравнение Навье-Стокса:

(13)

В более развернутой форме, после подстановки выражения для тензора скоростей деформаций имеем:

(14)

Это уравнение справедливо для общего случая движения жидкости – и когда жидкость сжимаема, и когда вязкость является переменной, . При этом второе и третье слагаемое правой части уравнения (14), градиент скалярной функции и дивергенция тензорной могут быть развернуты и дальше, пользуясь очевидными равенствами:

Если вязкость постоянна, , то уравнение (14) дает:

(15)

а если же к тому же жидкость и несжимаема, то имеем:

(16)

Уравнение Навье-Стокса (13) для общего случая движения жидкости может быть записано в дивергентном виде, раскрывая оператор материальной (эйлеровой) производной , а также представляя массовую силу в поле сил тяжести через ее потенциал , (если ось направлена вертикально вверх):

(17)

Для несжимаемой жидкости это уравнение упрощается :

(18)

В случае стационарного течения несжимаемой жидкости с постоянной вязкостью (случай становившегося течения жидкости с постоянными физическими свойствами) это уравнение принимает простой дивергентный вид:

(19)

Если объемная вязкость , т.е. ньютоновская жидкость не является стоксовой, то:

(20)

и вместо формулы (11) реологическим соотношением будет:

(21)

или, обозначая шаровую часть тензора напряжений через :

(22)

можно записать:

(23)

или

Взяв операцию получения следа для правой и левой частей этого выражения, получаем, как и в случае формулы (6):

(24)

или

т.е. имеем:

откуда скорость объемного расширения:

что совпадает с формулой (7).

Уравнение движения такой ньютоновской жидкости с объемной вязкостью будет:

(25)

где определено выражением (22).

В турбулентном режиме течения жидкости наиболее часто используется модель Буссинеска, согласно которой, наряду с вязкими напряжениями , определяемыми формулой (3), присутствуют еще и дополнительные, рейнольдсовы напряжения, которые для несжимаемой вязкой жидкости определяются тензором:

(26)

Здесь штрихи символизируют пульсации вектора скорости, длинная черта сверху – символ осреднения по Рейнольдсу [].

Замечание. Кроме осреднения по Рейнольдсу в теории турбулентности используют и осреднение по Фавру [], символом осреднения здесь является волнистая черта, а символами пульсаций – два штриха. Тогда, по Фавру, напряжение Рейнольдса определяется как:

Согласно модели Буссинеска для несжимаемой жидкости:

(27)

где - кинетическая энергия пульсаций, 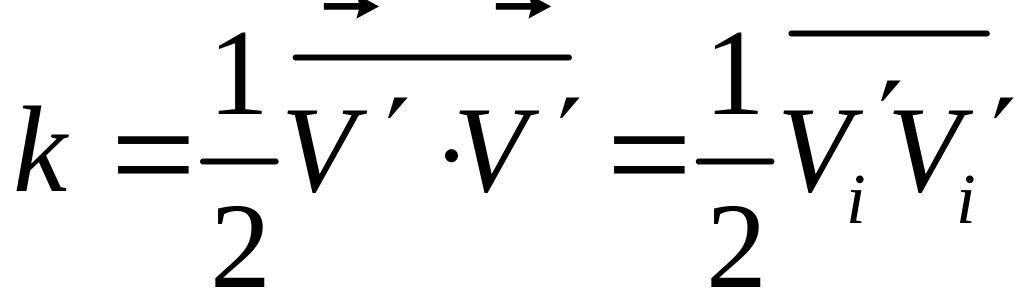; - турбулентная вязкость, которая зависит от поля скоростей; - тензор (осредненный) скоростей деформаций, , где скорости понимаются осредненными по Рейнольдсу.

В современных пакетах прикладных программ (FLUENT, ANSYS) тензор напряжений Рейнольдса записывают в несколько другом, отличном от (27) виде, пытаясь распространить модель Буссинеска и на случай движения сжимаемой жидкости. Тогда []:

(28)

След этого тензорного выражения показывает справедливость этого равенства:

Полный тензор напряжений , включает в себя член с давлением , вязкостное слагаемое и турбулентные напряжения Рейнольдса, т.е. этот тензор, в отличие от представления (1) имеет структуру:

(29)

С учетом соотношений (11) и (28), реологическим соотношениям для этого тензора будет в случае стоксовой жидкости, когда :

(30)

Введем понятие эффективной вязкости:

Тогда можно записать:

(31)

где

(32)

Операция взятия следа от правой и левой частей (31) дает, учитывая что содержит рейнольдсовы напряжения, для которых:

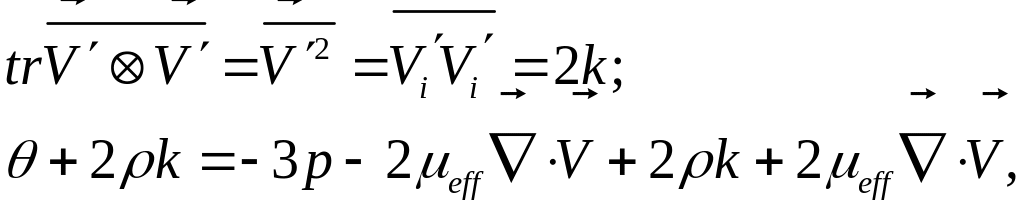
откуда следует, что , что и следовало ожидать для стоксовой жидкости.

Уравнение движения стоксовой ньютоновской жидкости в дивергентной форме будет:

(33)

Если же ньютоновская жидкость не является стоксовой, то и выражение сохраняет вид (31), но величина будет другой:

(34)

То же самое касается и уравнения движения жидкости с объемной вязкостью - оно сохраняет вид (33), однако величина определяется по соотношению (34). При этом операция взятия следа от правой и левой частей тензорного выражения (31) дает:

что приводит к соотношению

откуда скорость объемного расширения

(35)

что совпадает с выражением (7).

Замечание 1. Турбулентную вязкость , а следовательно и величину , а также кинетическую энергию пульсаций определяют по-разному, пользуясь разными моделями турбулентности [].

Замечание 2. Уравнение Навье-Стокса для тензора напряжений Рейнольдса , это напряжение присоединяют к вязким. Если же жидкость сжимаема, то возникают пульсации плотности – величина (кроме ), появляются помимо корреляций еще и другие, что усугубляет трудности в разрешении проблемы замыкания.