1.2. Векторы и тензоры. Базисные элементы декартовой прямоугольной системы координат

Рассмотрим трехмерное евклидово пространство. В нем можно выбрать базис – произвольную тройку некомпланарных векторов, соответствующих той или иной системе координат. Наиболее удобным и простым в использовании является базис декартовой прямоугольной системы координат , который и будем далее использовать. Этот базис является ортонормированным (ортогональным, т.е. базисные векторы взаимно перпендикулярны и нормированы – они имеют единичную длину). Удобство декартова прямоугольного базиса заключается в том, что векторы базиса не меняются при переходе от одной точки пространства к другой. Любой вектор в этом базисе может быть представлен в виде разложения по базису

(1.2.1)

где – проекции вектора на оси , соответственно, т.е.:

где точки являются символами скалярного произведения. На рис. 1.1 показан радиус – вектор произвольной точки с координатами , который в координатном виде записываются как

(1.2.2)

Очевидно, что координаты его суть проекции на оси, т.е.

Рис. 1.1. Декартова прямоугольная система координат.

В дальнейшем, для удобства, будем использовать индексную форму записи. Обозначим базисные векторы с помощью индексов 1, 2, 3. Тогда – первый базисный вектор, вторым будет , а третьим – . Соответственно компоненты радиус-вектора примут обозначения . Тогда вместо (1.2.2) можно записать:

(1.2.3)

а вместо (1.2.1):

(1.2.4)

Или, если использовать знак суммирования, эти выражения записываются в компактном виде следующим образом:

(1.2.5)

где индексы пробегают значения 1, 2, 3, т.е. по ним идет суммирование. Индексы могут быть обозначены и другими буквами, например 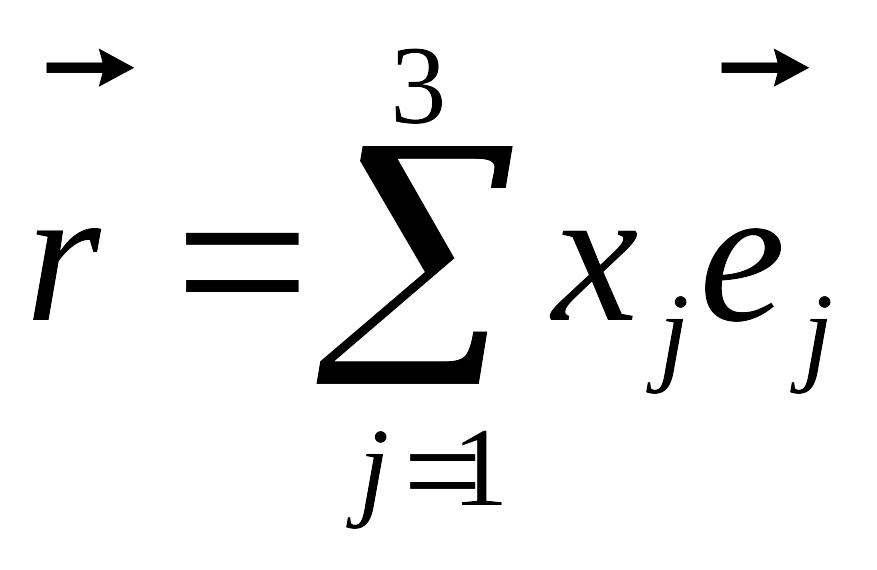, или 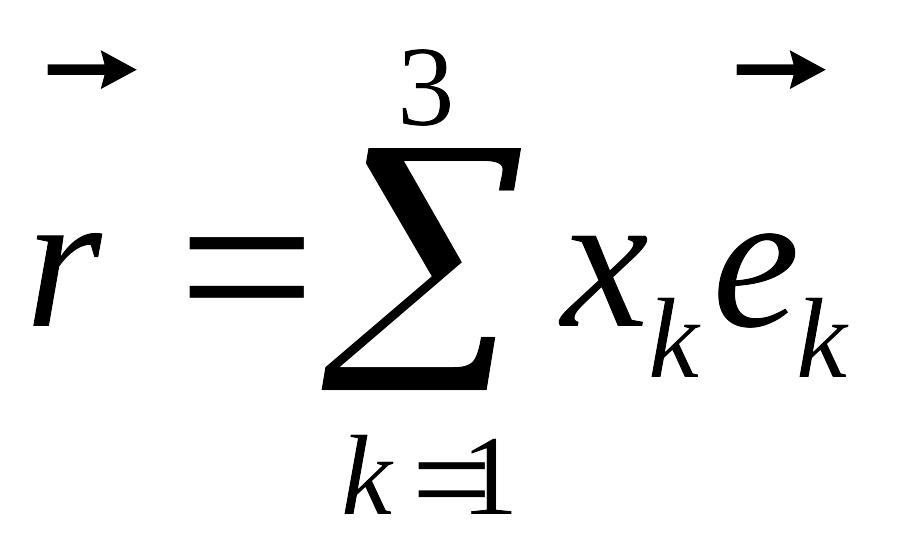и т.д.

По правилам индексных обозначений один и тот же индекс в каждом члене может встречаться или один, или два раза. Если индекс употреблен один раз, то подразумевается что он принимает одно из значений 1, 2, 3. Если же индекс употреблен дважды, как в выражениях (5), то используется правило суммирования:

Если в одночленном выражении один и тот же индекс используется дважды, то по нему происходит суммирование по значениям этого индекса 1, 2, 3. Индекс, по которому происходит суммирование, называется немым – его можно заменять на любой другой.

Используя правило суммирования, вместо выражений (1.2.5) можно записать:

(1.2.6)

или с другими немыми индексами:

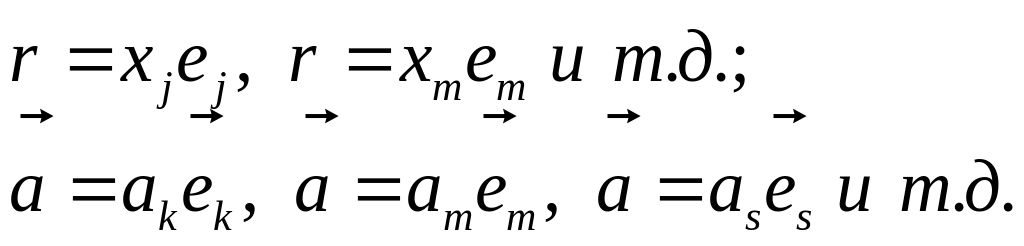
Вектор как геометрический объект трехмерного евклидова пространства представляет собой отрезок снабженный стрелкой. Абсолютную величину произвольного вектора обозначают просто . Сложение векторов подчиняется известному правилу параллелограмма (рис. 1.2 а):

В трехмерном евклидовом пространстве определена операция скалярного умножения векторов (точка символизирует эту операцию). Если вектор – еденичный, т.е. , то произведение есть проекция вектора на направление (рис. 1.2 б).

Рис. 1.2. Сложение и проектирование векторов

Для получения компонент вектора, как уже отмечалось, нужно ввести в рассмотрение базис . Для декартовой прямоугольной сстемы координат это ортонормированный базис. Это означает что скалярные произведения базисных векторов или 1, или 0 (так и т.д.). Отсюда следует, что эти произведения могут быть записаны через дельту Кронекера (1.1.1):

(1.2.7)

Тогда, имея базис , разложение вектора по базису будет:

(1.2.8)

где компоненты вектора вычисляются как результат проектирования на направления базисных векторов (т.е. как результат скалярного пороизведения вектора на базисный вектор ): . Действительно:

Но величина не равна нулю и равна единице тольео при . Следовательно,

Отсюда и следует:

(1.2.9)

т.е. для получения проекции вектора на направление базисного вектора нужно скалярно умножить этот вектор на базисный вектор.

Примеры: запишем в компонентном виде выражения и :

или, более подробно, в обычном виде:

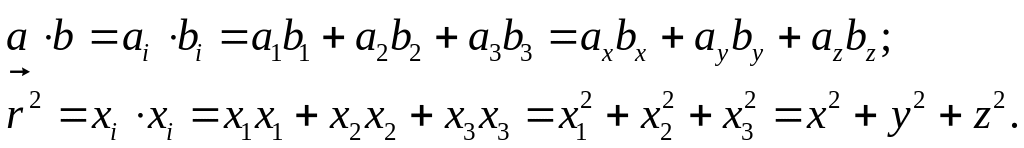
Примечание. Записывать в виде нельзя, т.к. в этом случае исчезает возможность применения правила суммирования по повторяющемуся индексу. В этом случае величина обозначает не сумму, а одно из трех значений – или , или , или .

В трехмерном евклидовом пространстве паре векторов и можно сопоставить:

– скалярное произведение (скаляр);

– векторное произведение (вектор);

– тензорное произведение (тензор второго ранга), – знак тензорного произведения.

Для скалярного произведения векторам и сопостовляется число:

или, если выбран базис:

Модуль вектора по определению

Используя погятие векторного произведения векторов можно паре векторов и сопоставить вектор

где – еденичный вектор, перпендикулярный плоскости векторов и и направленный для правоориентированного пространства так, что глядя с его конца мы видим поворот вектора к вектору по кратчайшему расстоянию против часовой стрелки (рис.1.3).

Рис.1.3. Векторное произведение.

Запись векторного произведения через компоненты в выбранном базисе затруднена. Действительно

но величину – векторное произведение базисных векторов – можно будет записать через базисные элементы только после введение в рассмотрение тензора третьего ранга – тензора Леви–Чивита.

Примечание. Иногда в литературе скалярное произведение векторов записывают, применяя круглые скобки – , а векторное – прямые .

Смешанное произведение трех векторов дает объем параллелепипеда, построенного на этих векторах:

Скалярное и векторное произведения можно менять местами. А так как векторное произведение выполняется первым, то скобки можно опустить и записать:

В литературе такое произведение часто обозначают просто как .

Наряду со скалярным произведением векторов и можно ввести в рассмотрение тензорное (диадное) произведение их: (диады и , вообще говоря, различны). В результате паре элементов исходного трехмерного евклидова пространства сопоставляется единственным образом некоторый элемент трехмерного тпространства . Это соответствие является биленейным:

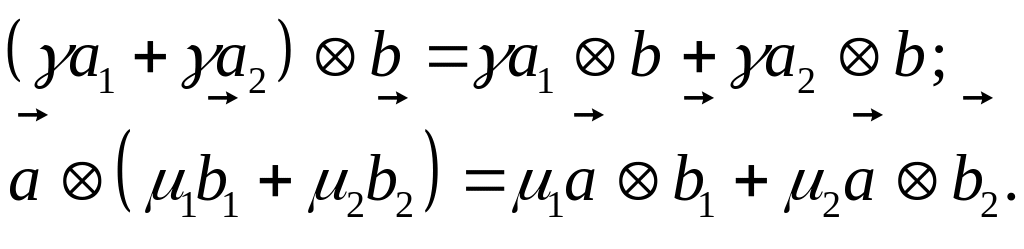
Базис нового (тензорного) пространства представляет собой тензорпные произведения (диады) элементов исходного базиса:

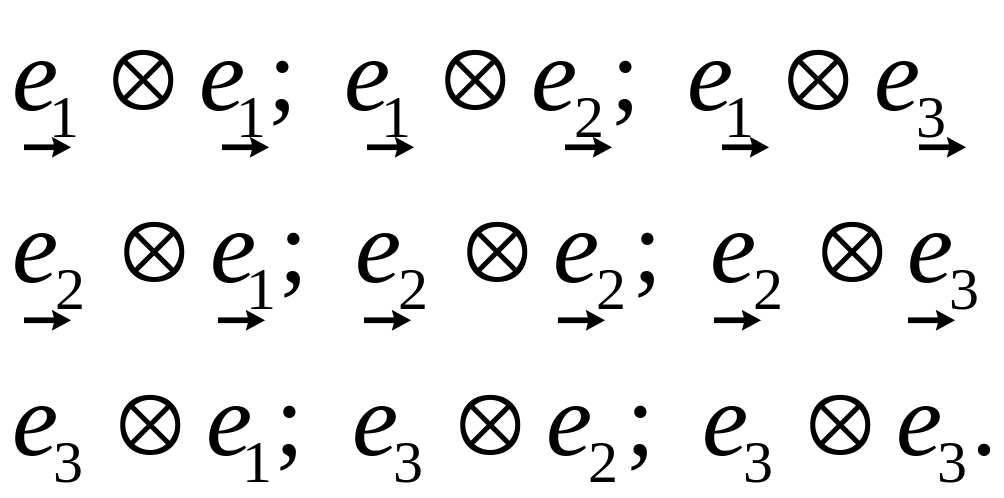
Элементы пространства называются тензорами второго ранга и представляют собой линейные комбинации относительно элементов тензорного базиса. Разложим тензор второго ранга по элементам этого базиса:

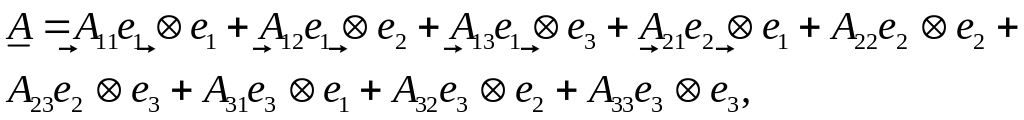(1.2.10)

или, в компактном виде, используя правило суммирования:

(1.2.11)

Замечание. Знак диадного произведения мложно опускать и записывать (можно и как б и как и т.д.).

Геометрический тензор второго ранга заключается в следующем – он переводит векторы в векторы (рис. 1.4).

Рис. 1.4. Смысл тензора – перевод вектор в вектор.

На вектор подействовали тензором и получили другой вектор – вектор . Аналитически это записывается следующим образом:

(1.2.12)

Покажем что это так, записывая левую часть в компонентном виде:

Но величина есть –тая величина компоненты некоторого вектора, который обозначим как , следовательно

Компоненты тензора находятся легко, если выбран базис . Тогда для представления тензора в компанентном виде как его компоненты могут быть найдены умноржением скалярно базисных векторов на слева и справа:

(1.2.13)

Действительно:

Здесь учтено, что дельты Кронекера и не равны нулю и равны единицам только при равенстве значений индексов, т.е. при и .

Каждому тензору второго ранга соответствует его матрица компонент:

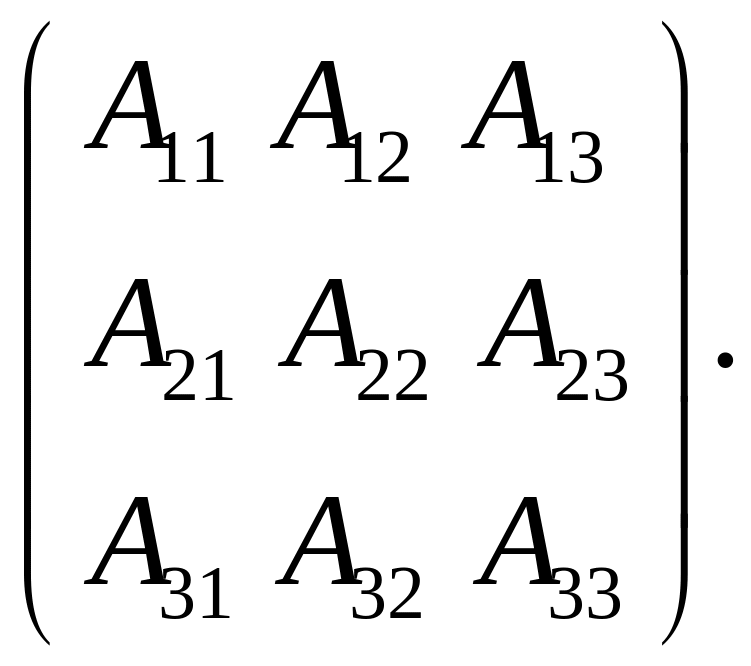(1.2.14)

Единичный тензор (тензорная единица) является тензором второго ранга, он имеет своими компонентами дельту Кронекера:

(1.2.15)

Он переводит вектор сам в себя, скалярное произведение произвольного тензора на единичный тензор не меняет этот тензор. Матрица компонент единичного тензора имеет вид:

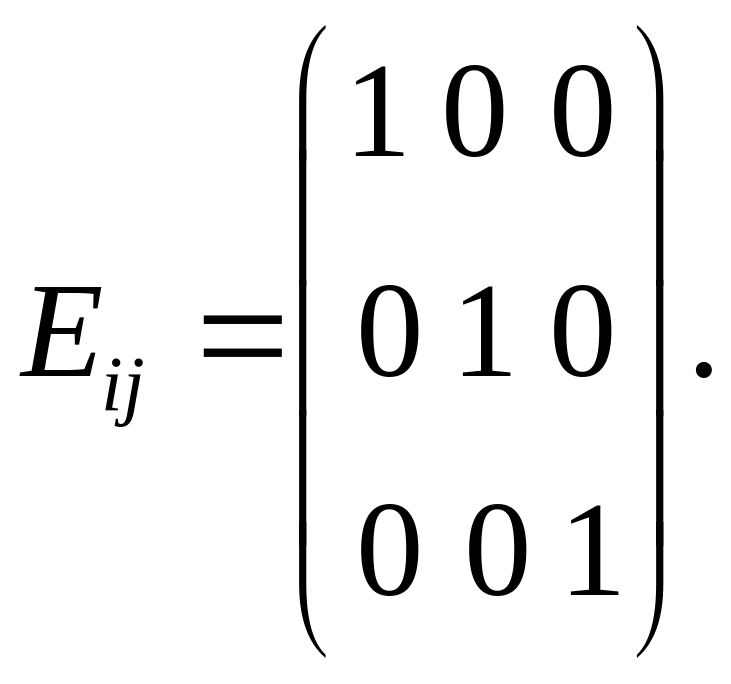(1.2.16)

Тензоры более высоких, нежели второго, рангов можно в компонентном виде записывать через базисные полиады. Так, тензор третьего ранга в качестве базисных элементов имеет базисные триады, тензоры четвертого ранга – базисные тетрады и т.д.:

(1.2.17)

(1.2.18)

Здесь слева у обозначения тензора помечен его ранг (не путать обозначения для тензора третьего ранга с – кубом тензора второго ранга). Видно, что тензор третьего ранга имеет 27 компонент, тензор четвертого ранга – 81 компоненту и т.д. Заметим, что в механике жидкости, тензоры ранга больше четырех не используются, они не имеют физического смысла.