2.8. Материальные производные в уравнениях переноса и их дивергентный вид.

Умноженную на плотность материальную (Эйлерову) производную любой физической величины (скалярной, векторной, тензорной) всегда можно представить в «дивергентном» виде:

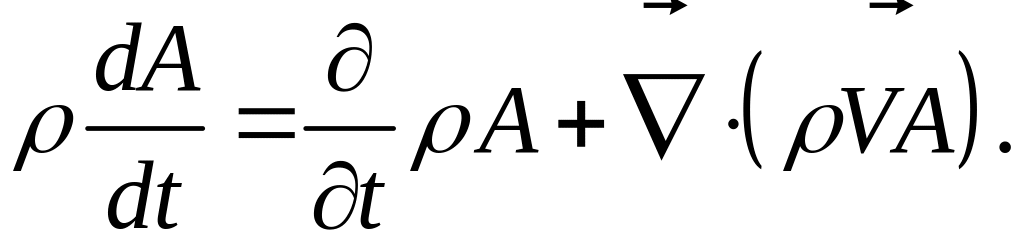
Это следует из уравнения неразрывности.

Примеры:

1) Величина является скалярной, например температурой Тогда

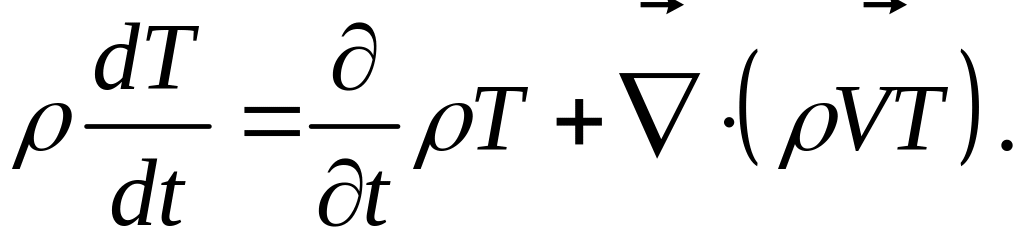
Докажем это равенство, расписывая в компонентном виде левую и правую части этого равенства. Для левой части имеем:

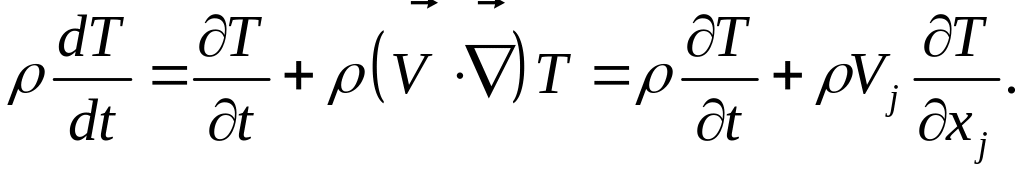
Для правой части:

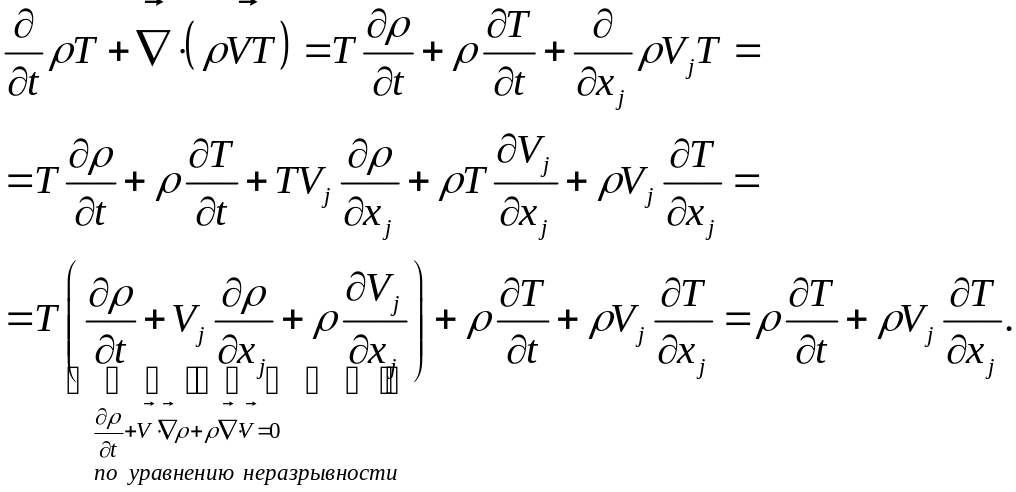
Поскольку выражение в скобках равно нулю (оно представляет собой запись равнения неразрывности), то равенство левой и правой частей очевидно.

2) Величина является векторной, например скоростью Тогда материальную производную (ускорение жидкой частицы, локальное и конвективное) можно представить в виде:

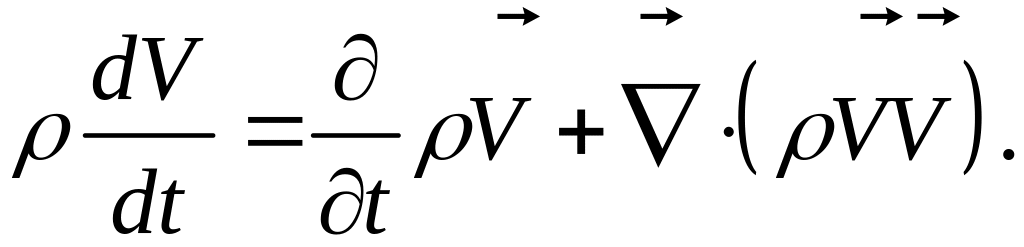
Здесь под знаком дивергенции находится тензор тензор потока импульса, знак тензорного умножения опущен, для простоты записи. докажем это тождество, используя на заключительном этапе выкладок уравнение неразрывности. Для этого распишем обе части тождества в компонентном виде. Левая часть:

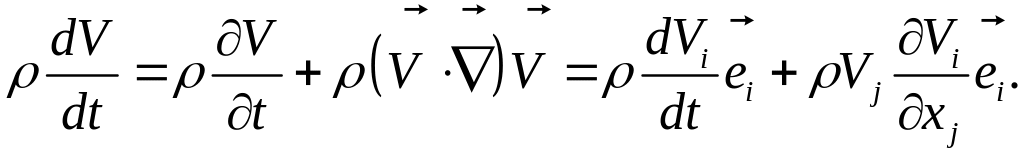
Правая часть, второе слагаемое:

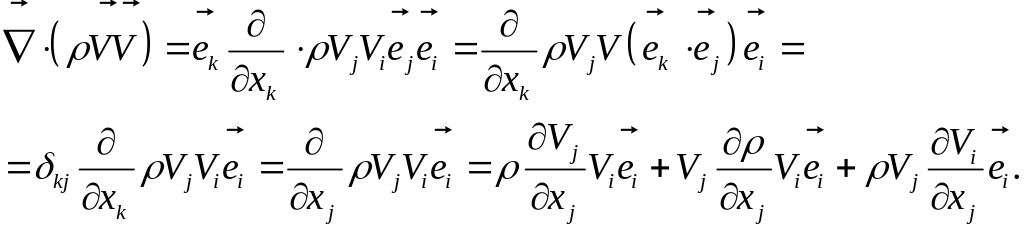
Первое слагаемое правой части:

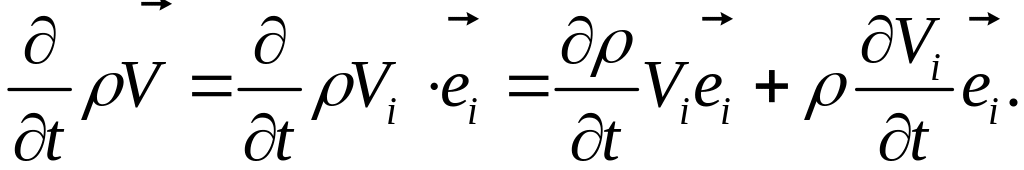
В целом, правая часть после группировки:

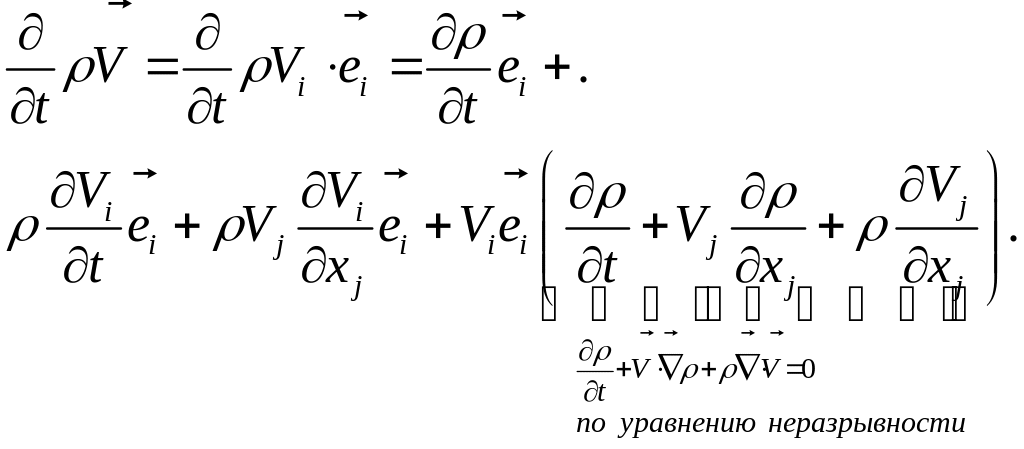
Поскольку выражение в скобках равно нулю по уравнению неразрывности, то тождество верно и для случая, если является векторной величиной.

3) Пусть величина является тензорной, например тензором напряжений Этот симметричный тензор второго ранга в декартовой прямоугольной системе координат представим в виде:

Докажем равенство:

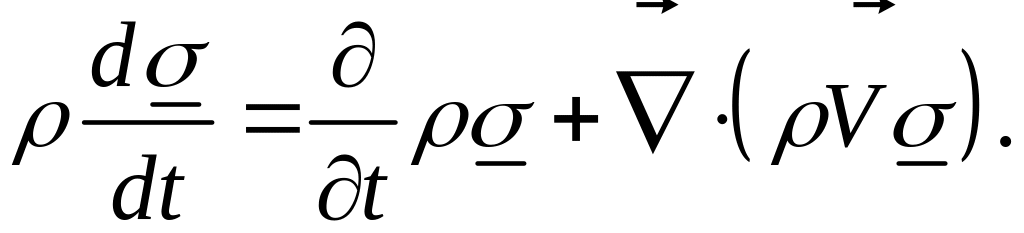
Запишем левую и правую части в компонентном виде. Левая часть, являющаяся, как и правая, тензорами второго ранга:

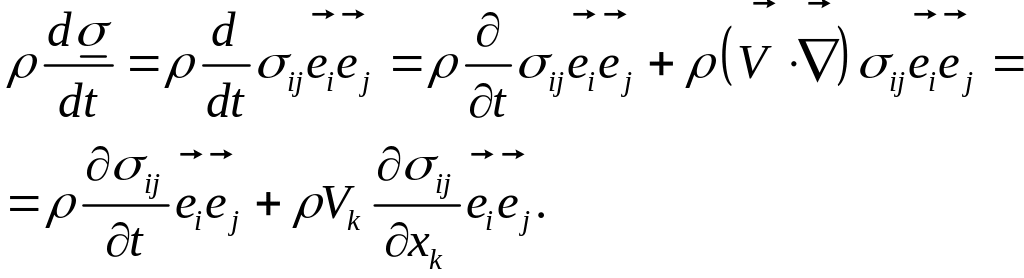
Правая часть:

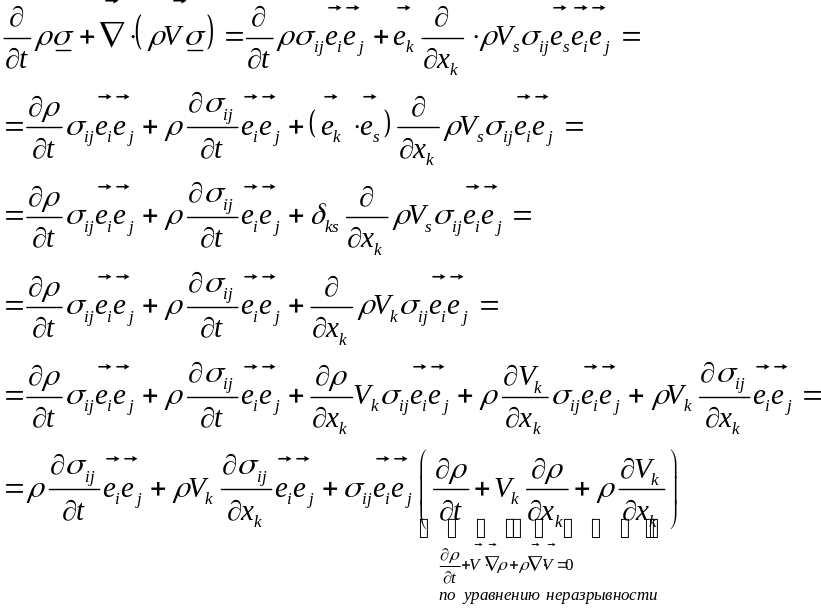
И здесь, для тензорной величины, видна справедливость тождества.

Замечание: Величина 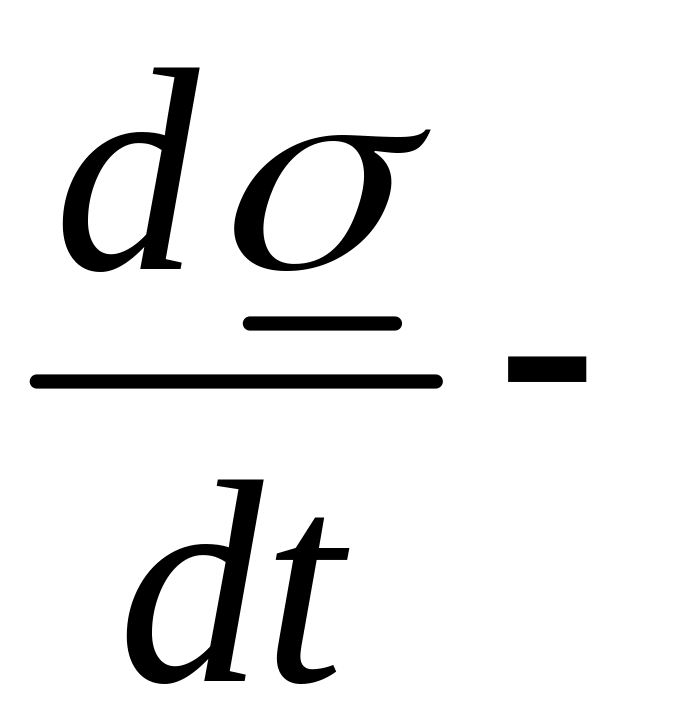материальная, Эйлерова производная, которая состоит из локальной и конвективной частей:

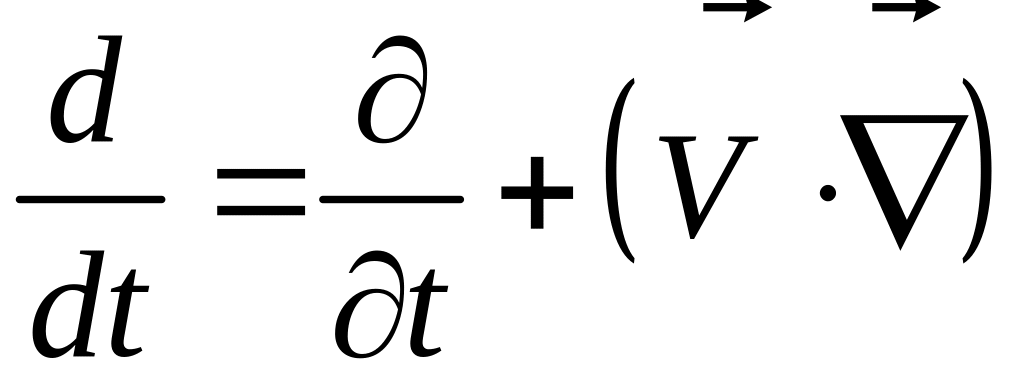
может, на первый взгляд, использоваться в моделях жидкости, при записи определяющего уравнения в виде дифференциального уравнения переноса []. Однако, внимательный анализ показывает, что Эйлерова производная тензора второго ранга не является инвариантной величиной []. Поэтому вместо производной в качестве материальной производной для тензора второго ранга выступает производная , содержащая, кроме локальной и конвективной, еще и вращательную часть.

Вращательную часть привести к дивергентному виду невозможно.

Материальная, конституитивная производная тензора второго ранга.

Как известно [], вид материальной производной зависит от ранга тензора. Это связано с необходимостью обеспечить нейтральность, относительно поворотов системы отсчета для производных тензоров. Материальная (Эйлерова) производная , содержащая локальную и конвективную части, после применения ее к скалярным и векторным функциям дает нейтральные объекты, но если эту производную применить к тензору второго ранга, то нейтральность нарушается, появляется некоторая добавка [], которую можно компенсировать, убрать, если к локальной и конвективной частям материальной производной добавить вращательную часть. Такая материальная производная называется конституитивной и обозначается как . Вид вращательной производной, добавляемой к , может быть разный, несколько отличающимся друг от друга.

Известны вращательные производные для произвольного тензора второго ранга :

-Яуманна, ее вид , где антисимметричный тензор вращения;

-Ривлина, ее вид

-Олройда, Седова и другие [].

Наиболее распространенной является вращательная производная Яуманна. Соответствующая материальная производная Яуманна, для произвольного тензора второго ранга имеет вид:

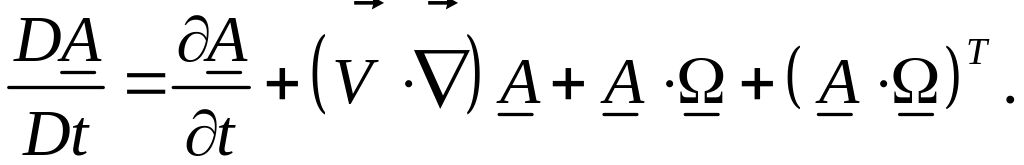
Материальная производная Ривлина записывается следующим образом:

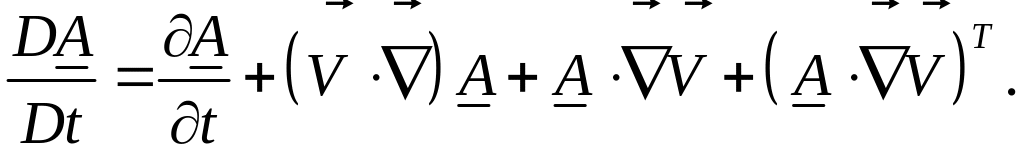
Видно, что производная Ривлина отличается от производной Яуманна добавкой , которая является нейтральной и не играет роли при исправлении не нейтральности .

Замечание: Вращательная производная симметричного тензора также является симметричным тензором. Для примера рассмотрим вращательную производную тензора скоростей и деформаций:

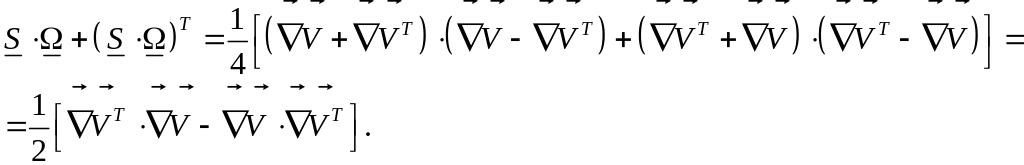
Получили симметричный тензор второго ранга.

Замечание: Конвективные производные физических величин можно привести к дивергентному виду. Вращательные производные тензорных величин к такому виду провести невозможно.

О дивергентном виде.

Часто требуется для проведения вычислительных процедур придать тому или иному слагаемому соответствующего уравнения дивергентный вид. Для градиента скалярной функции можно записать:

(1)

- для градиента вектор-функции

(2)

- для ротора вектор функции:

(3)

где тензор Леви-Чивита;

- для лапласиана функций:

(4)

Докажем эти соотношения. Для градиента скалярной функции рассмотрим дивергенцию тензора

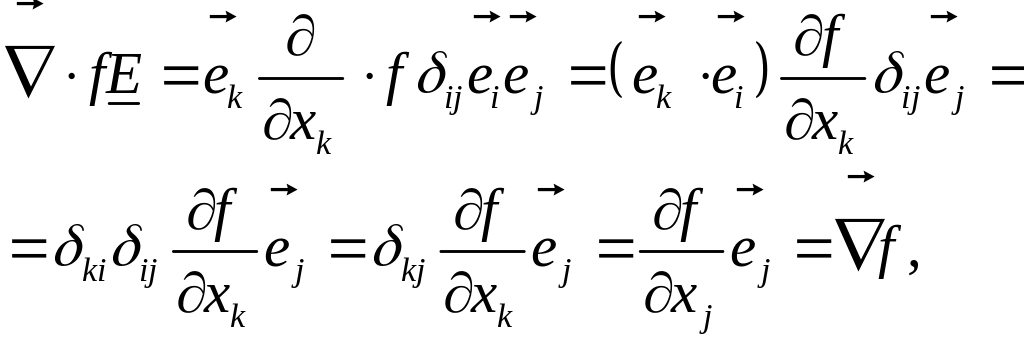
получили вектор-градиент скалярной функции.

Для соотношения (2) дивергенция тензора третьего ранга дает:

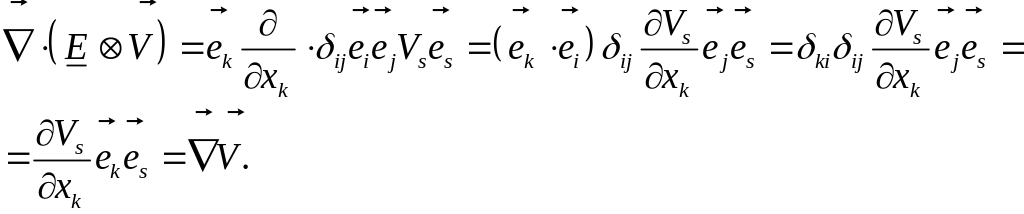
Получили тензор-градиент вектора.

Замечание: Совсем другой результат дает Действительно

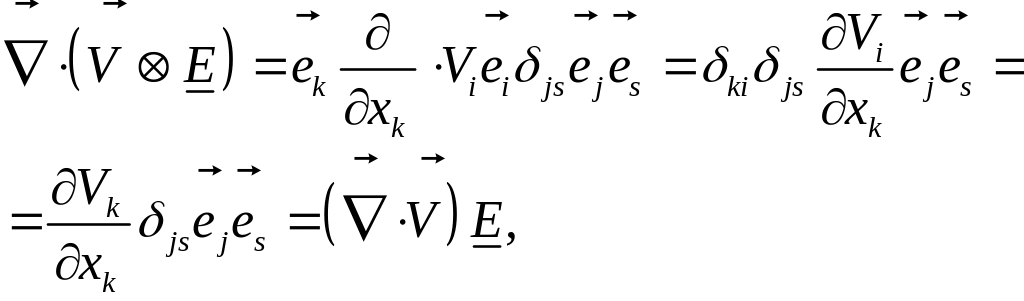
Получили шаровой тензор. Матрица компонент этого тензора

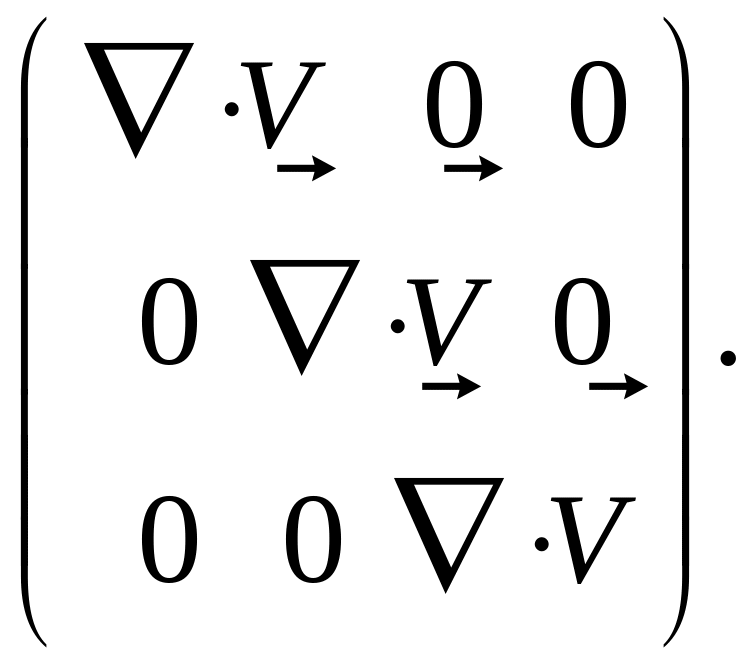
Для доказательства (верности/правильности?) соотношения (3) рассмотрим дивергенцию тензора второго ранга

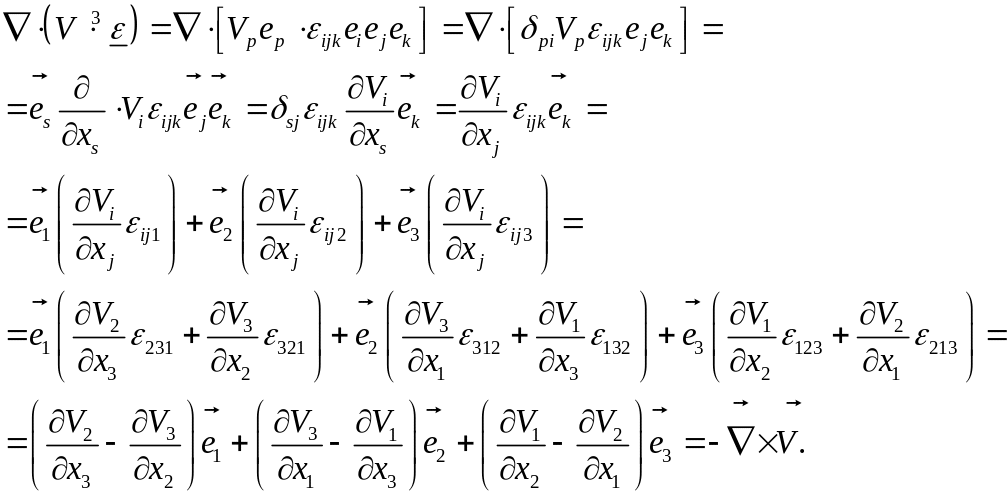
Любопытно заметить, что тот же результат дает

Формулы (4) не требуют громоздких доказательств:

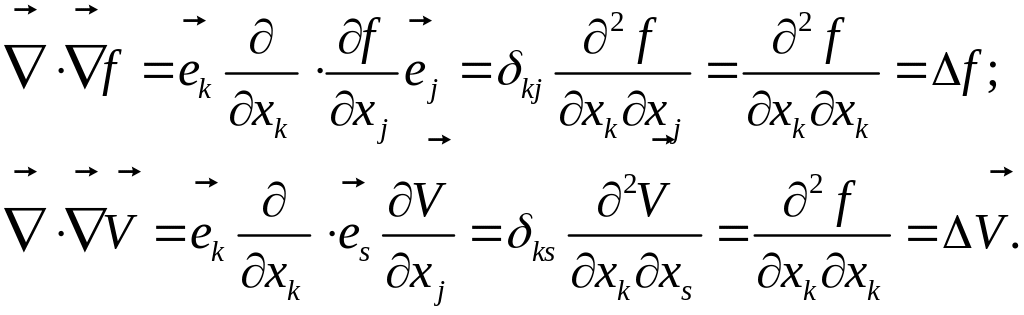
Пользуюсь этими соотношениями, многие формулы могут быть записаны в дивергентном виде. Например, известная [] формула для т.е.

может быть записана в виде:

(5)

Скалярной функции может быть сопоставлен вектор что очевидно из определения вектора . Этой функции может быть сопоставлен и те тензоры второго ранга:

- симметричные и

- антисимметричный

Их матрицы компонент, соответственно:

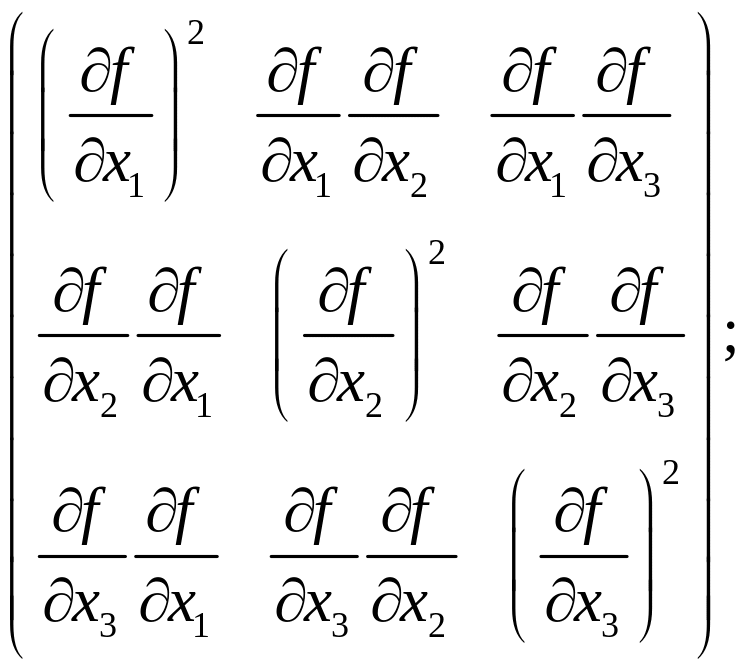
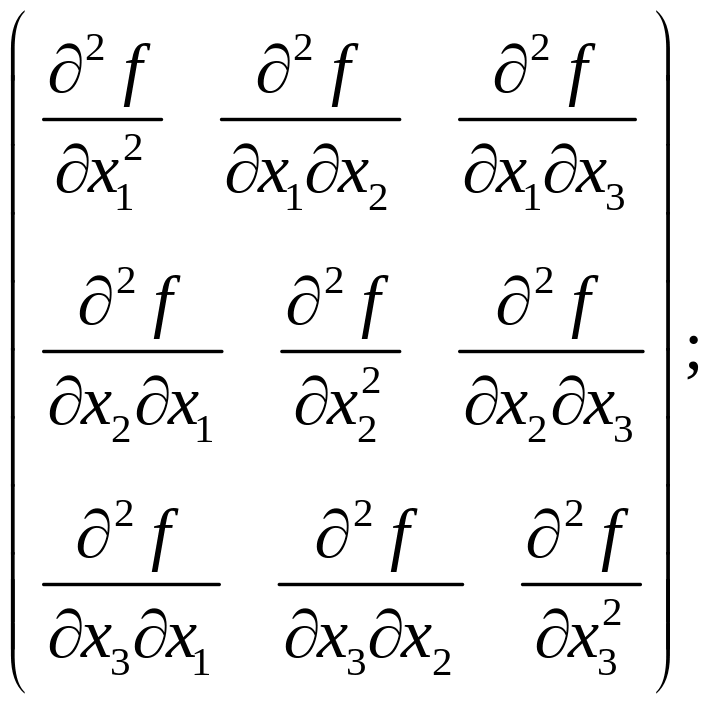
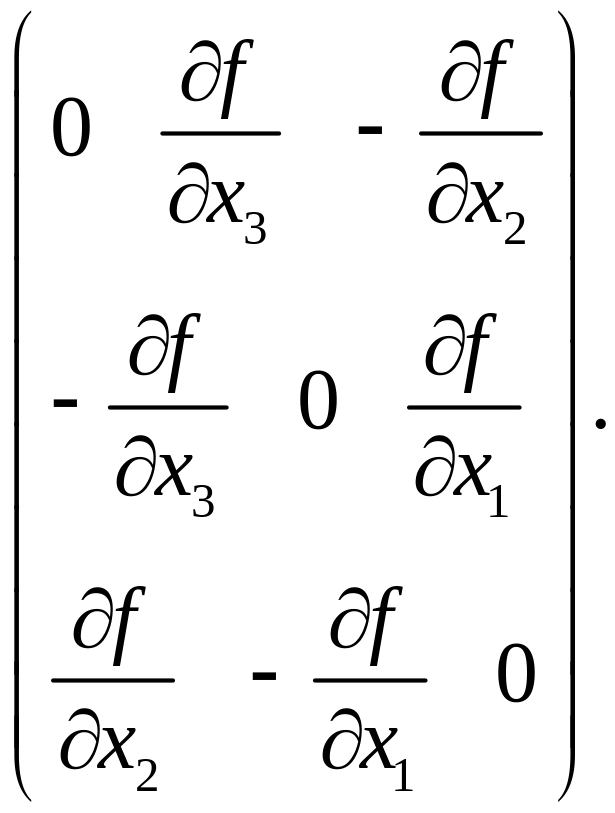
Также антисимметричным тензором второго ранга является и другая форма записи , его можно записывать как . Но эта форма записи уже не имеет дивергентного вида. Таким образом имеем:

(6)

Примечание: Интересно заметить, что:

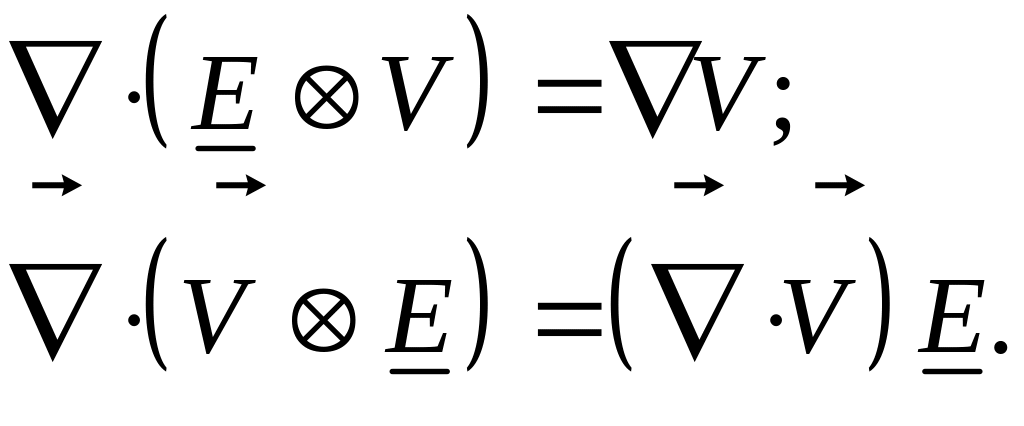
При выводе уравнения Бернулли в уравнении Эйлера для идеальной жидкости нужно представить член 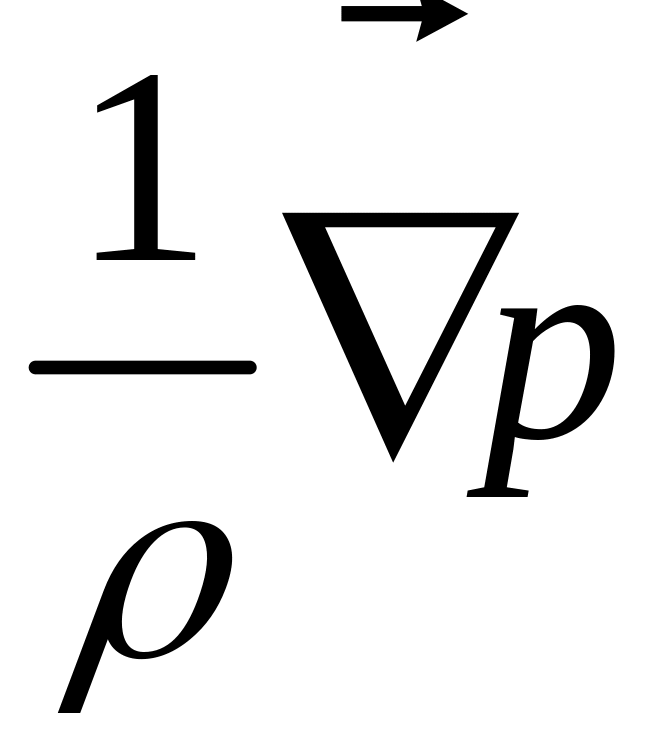в градиентной форме, в виде некоторого градиента. Если жидкость несжимаемая, то очевидно

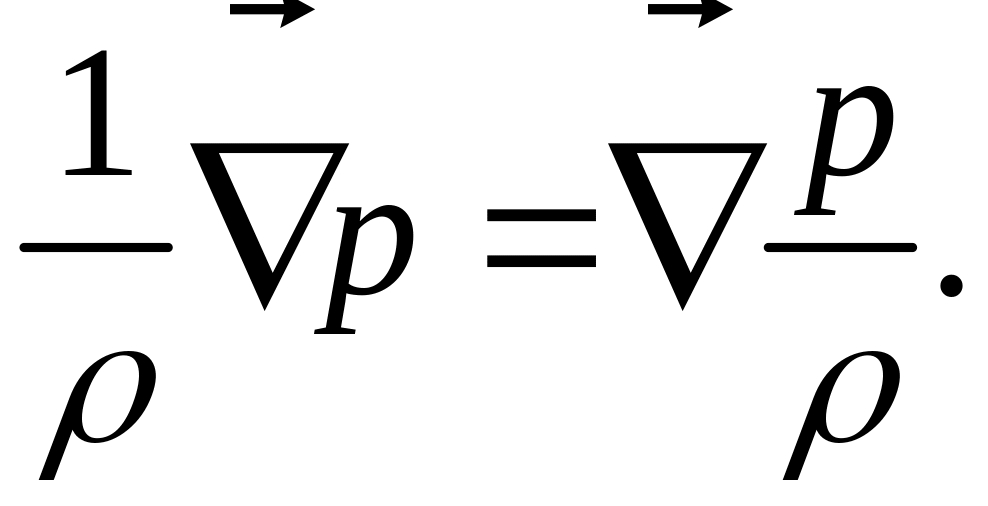(1)

Если же имеет место течение газа, который будем считать совершенным (т.е. подчиняющимся закону Менделеева-Клайперона, при чем показатель адиабаты ), то обычно вводят в рассмотрение, если движение баротропное, баротропную функцию (функцию давления):

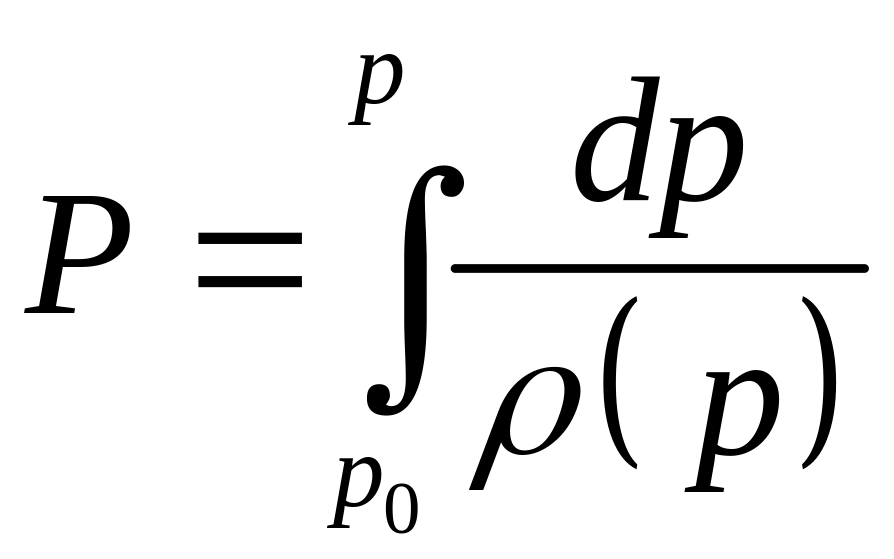(2)

и правую часть в выражении (1) записывают в виде

Однако слагаемое можно записать и по-другому, используя очевидное равенство:

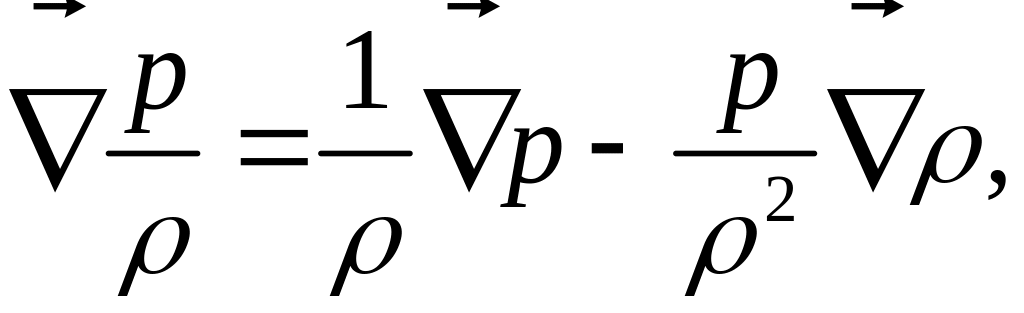
откуда следует:

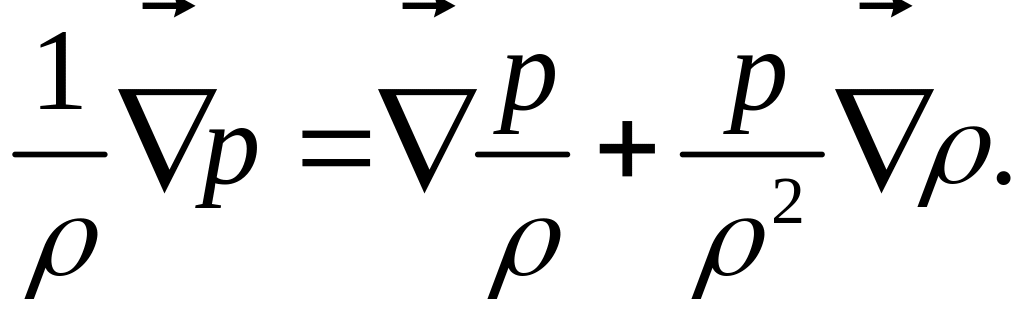(3)

Видно, что свойство сжимаемости приводит по сравнению с выражением (1) к добавочному слагаемому 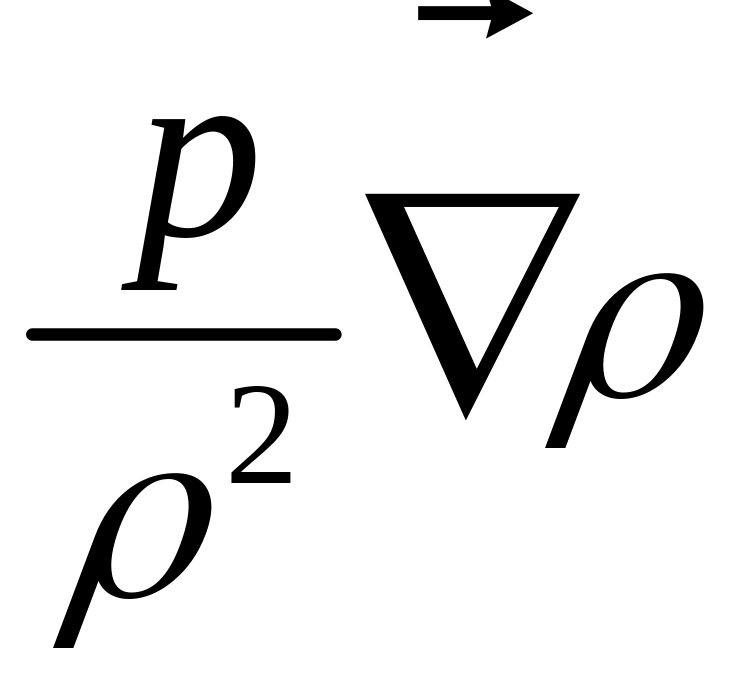, которое также можно привести к дивергентному виду.

При изотермическом движении совершенного газа:

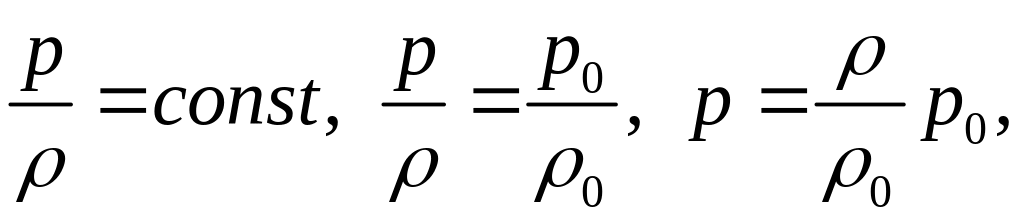
где параметры газа в некоторой фиксированной точке.

Тогда добавочное слагаемое:

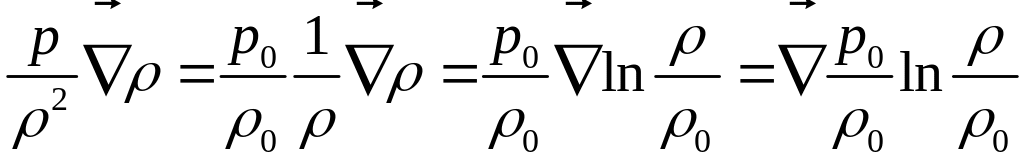
и формула (3) приобретает вид:

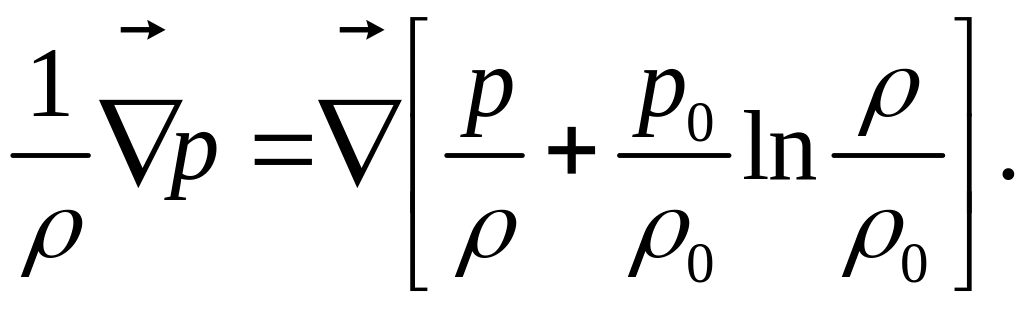(4)

Поскольку первое слагаемое в скобках является константой, то окончательно имеем:

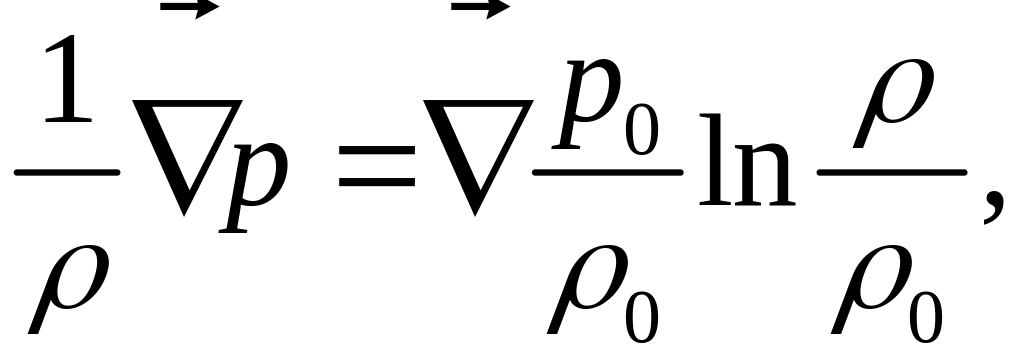(5)

или что тоже самое:

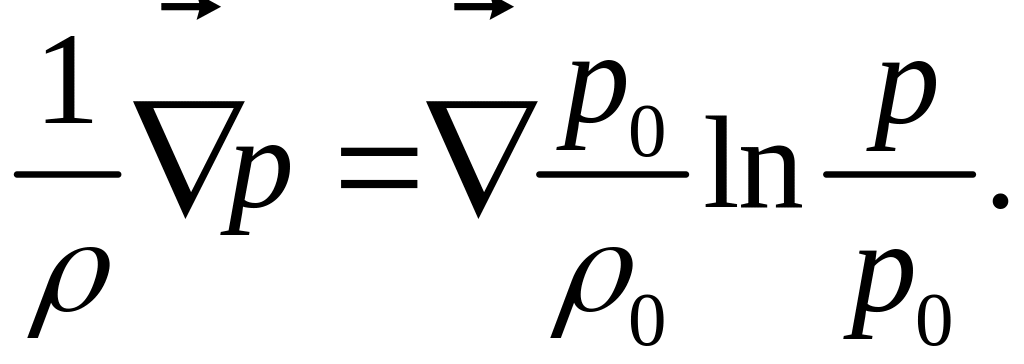(6)

В итоге уравнение Бернулли для изотермического течения идеального газа принимает вид:

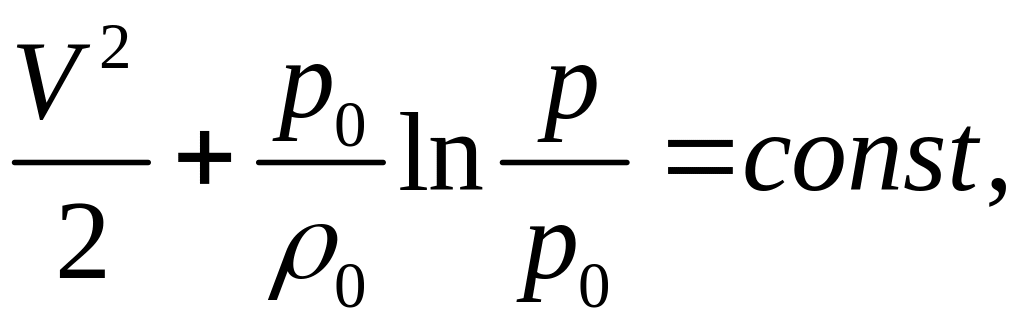(7)

или, учитывая что в фиксированной точке с параметрами на рассматриваемой линии тока скорость частицы газа равна :

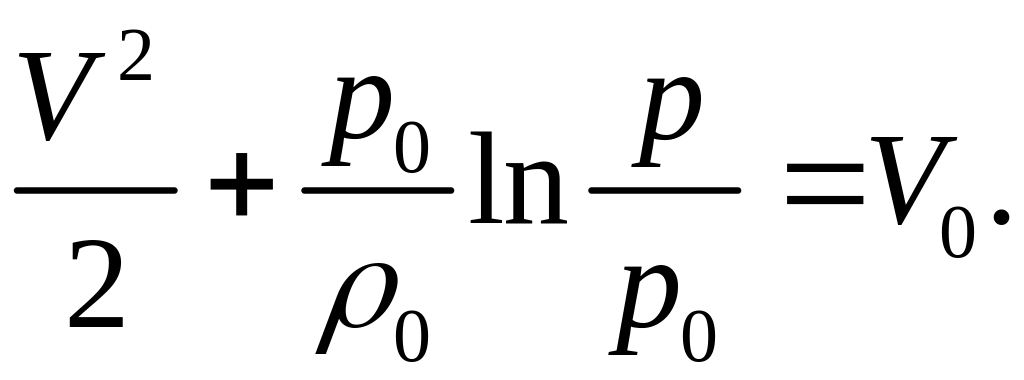
Для адиабатического движения совершенного газа, когда:

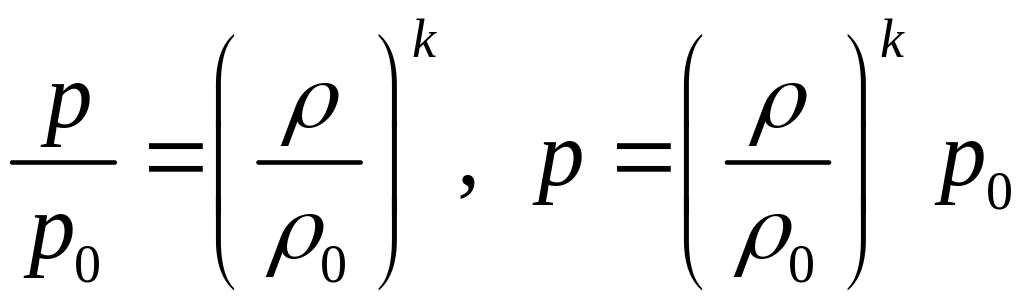
добавочное слагаемое в формуле (3) принимает вид:

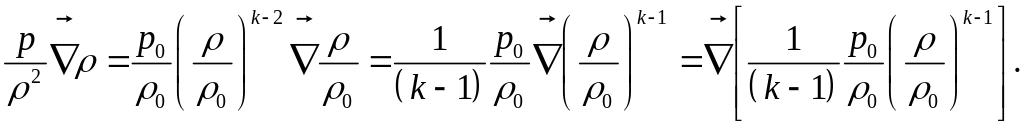(8)

Тогда формула (3) для этого случая течения приобретает вид:

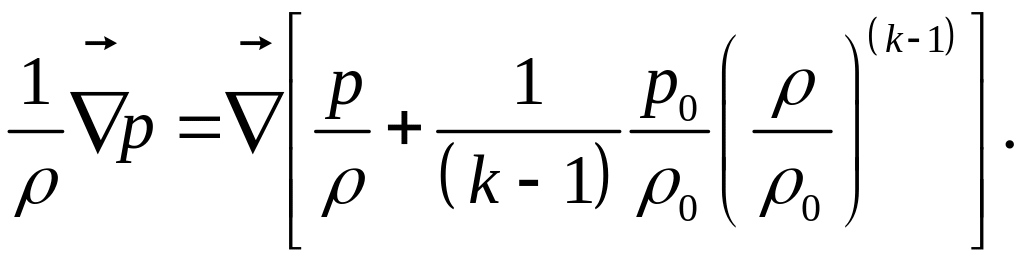(9)

Поскольку первое слагаемое в скобках можно представить в виде:

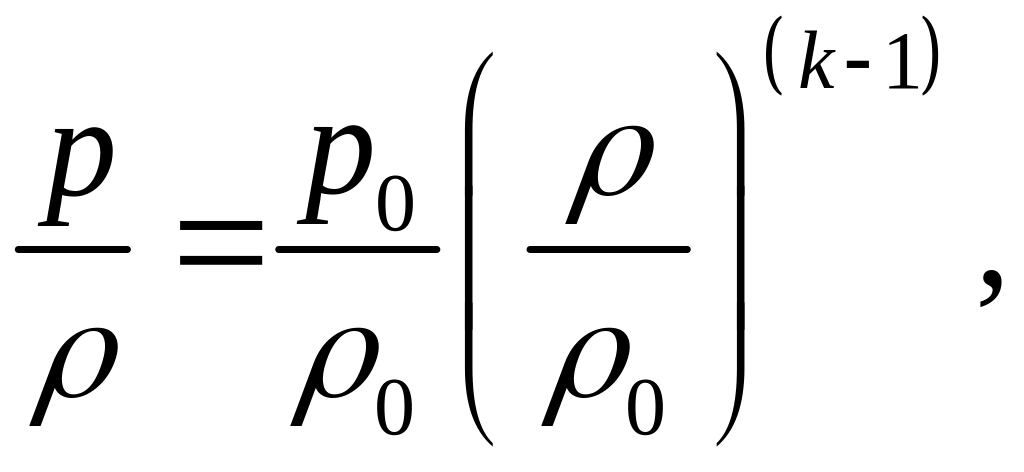
то формула (9) запишется как:

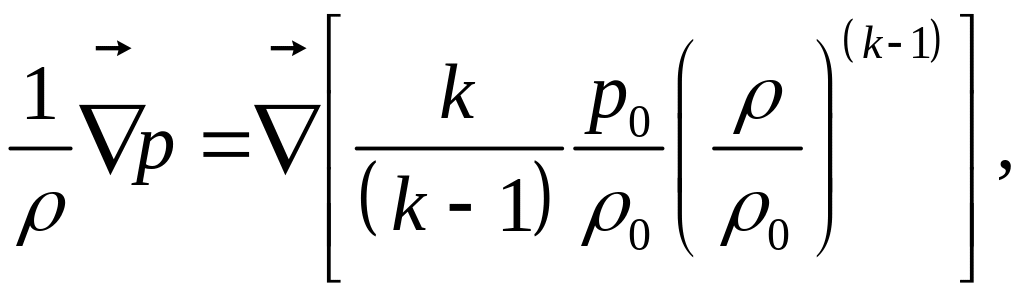
или, через изменения давления:

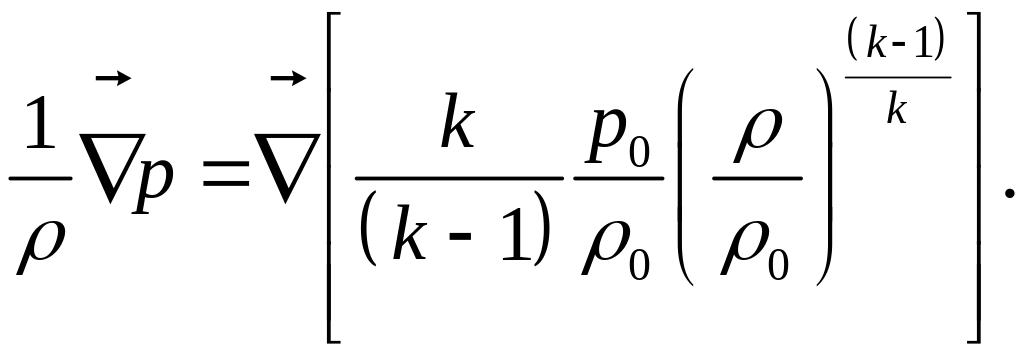
В итоге уравнение Бернулли для струйки совершенного газа при его адиабатическом движении имеет вид:

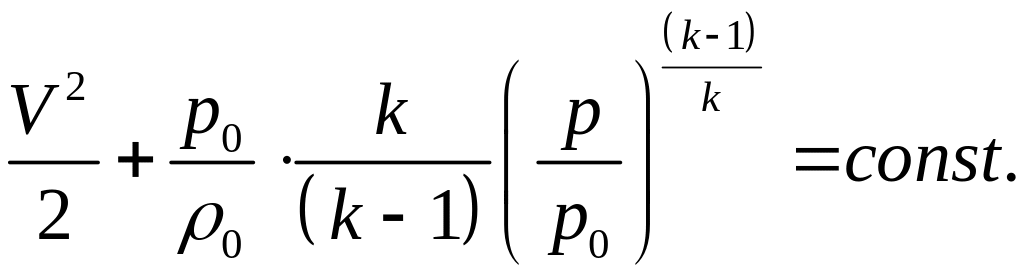(10)

Тогда, учитывая что в фиксированной точке на данной линии тока с параметрами скорость , уравнение (10) будет:

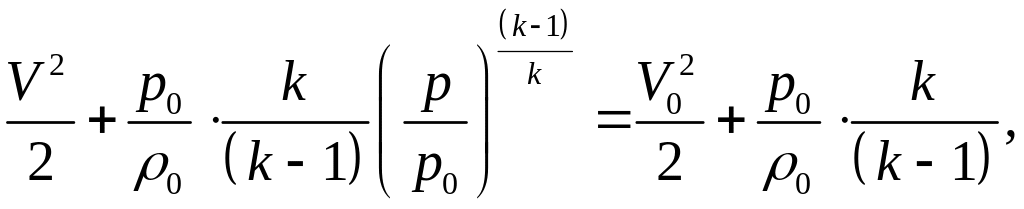
или, в несколько другом виде:

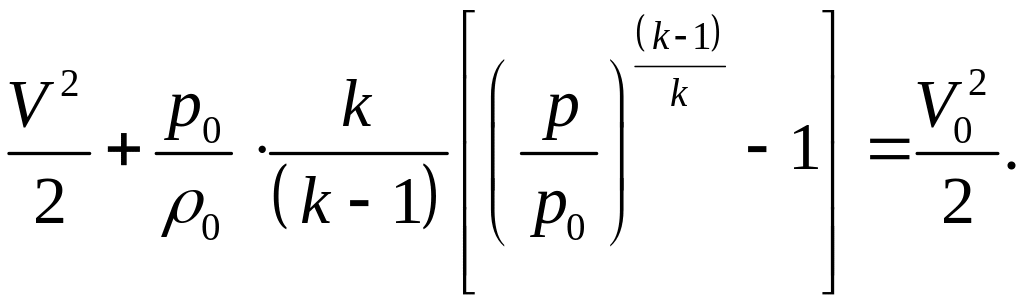(11)

Для задачи истечения газа из бесконечно большого объема, когда , имеем формулу Сен-Венана и Ванцеля:

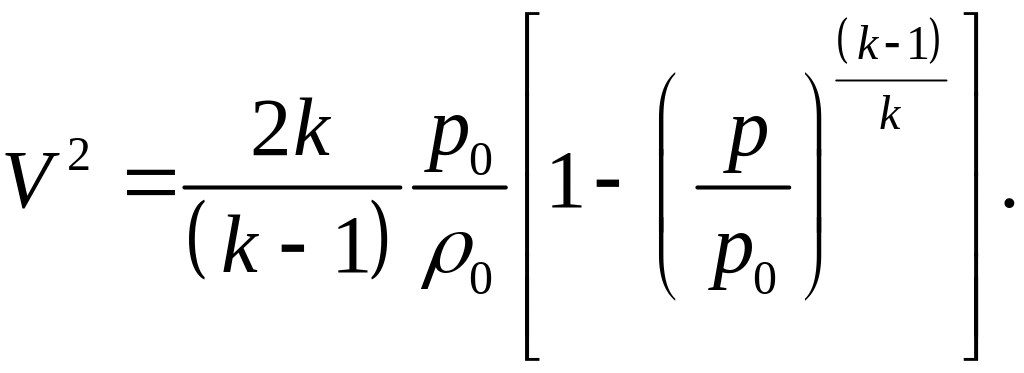(12)

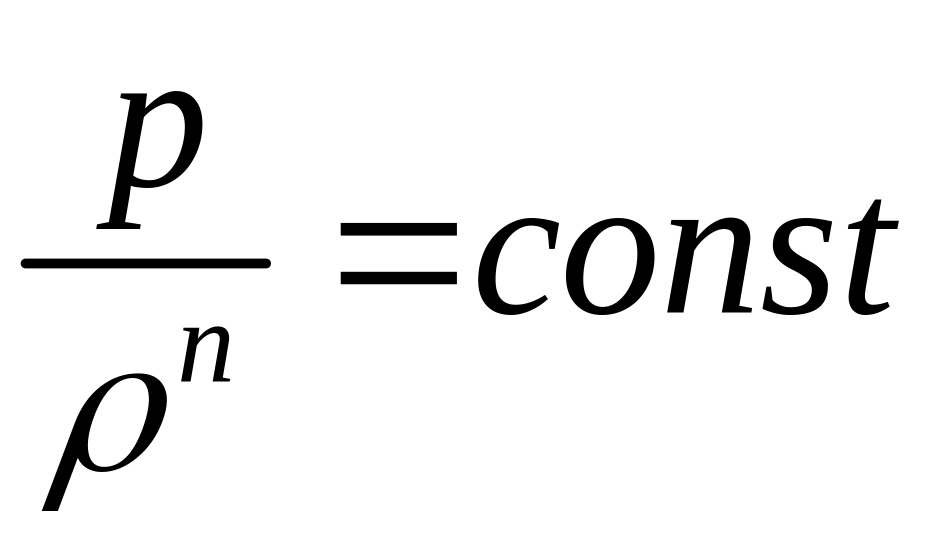Для политропного процесса с показателем политропы и уравнением имеют место формулы (8) – (12), в которых показатель адиабаты заменен на показатель политропы .