3.4. Общая схема исследования функции и построение ее графика

В различных учебниках рекомендуются общие схемы исследования функции, отличающиеся лишь в деталях. Можно предложить следующий план исследования.

1. Найти область определения функции.

2. Найти точки разрыва (если они есть) и определить их род.

3. Определить четность, нечетность, периодичность функции.

4. Найти точки экстремума и интервалы монотонности (эти два элемента поведения функции определяются, как правило, одновременно).

5. Найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.

6. Найти асимптоты графика функции.

7. Для получения графика функции в некоторых случаях полезно найти несколько точек (например, точки пересечения с осями координат), определить поведение функции при .

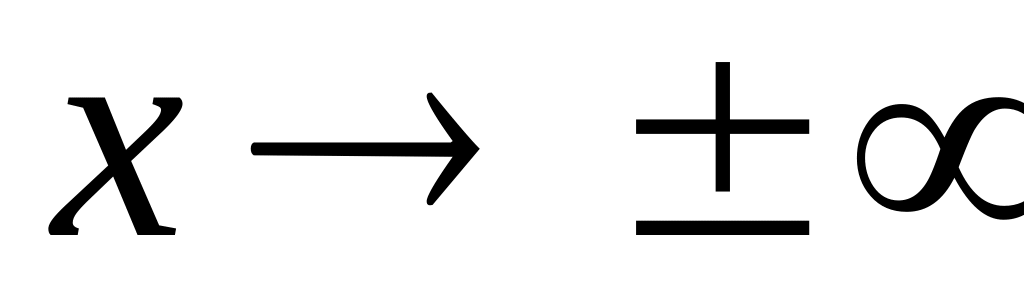На основании исследования функции нетрудно построить ее график. При его построении рекомендуется сначала нанести на координатную плоскость найденные точки графика и изобразить график в окрестности точек экстремума.

Пример. Исследовать функцию и построить ее график.

Решение.

1. Функция определена во всех точках, кроме 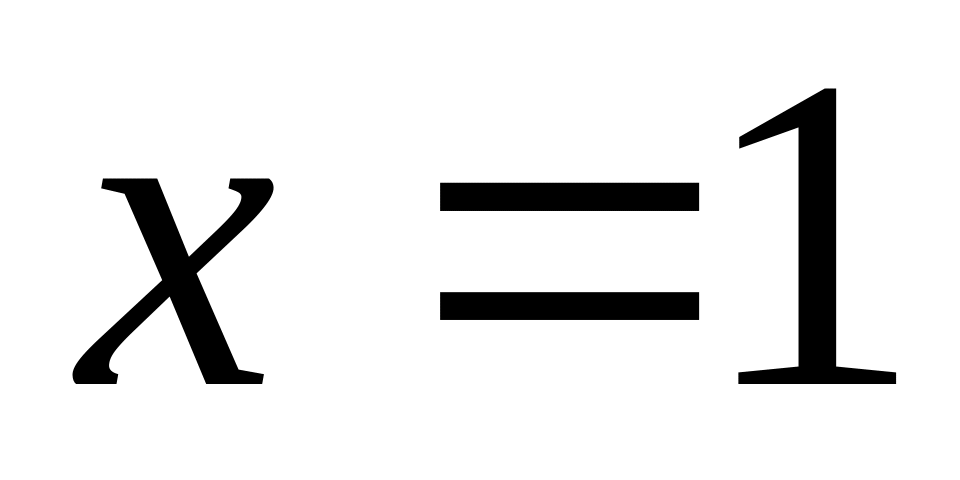, т.е. область определения составляет множество .

2. В точке функция разрывна. В остальных точках функция непрерывна.

3. Условия четности и нечетности не выполняются

,

.

Функция не является ни четной, ни нечетной. Это функция общего вида. Следовательно, график функции не симметричен ни относительно оси , ни относительно начала координат. Функция непериодическая (что очевидно).

4. Найдем экстремум функции и интервалы монотонности:

.

: ; .

Отсюда , .

Производная не существует в точке , но в этой точке не существует и сама функция.

Исследуем критические точки:

						+
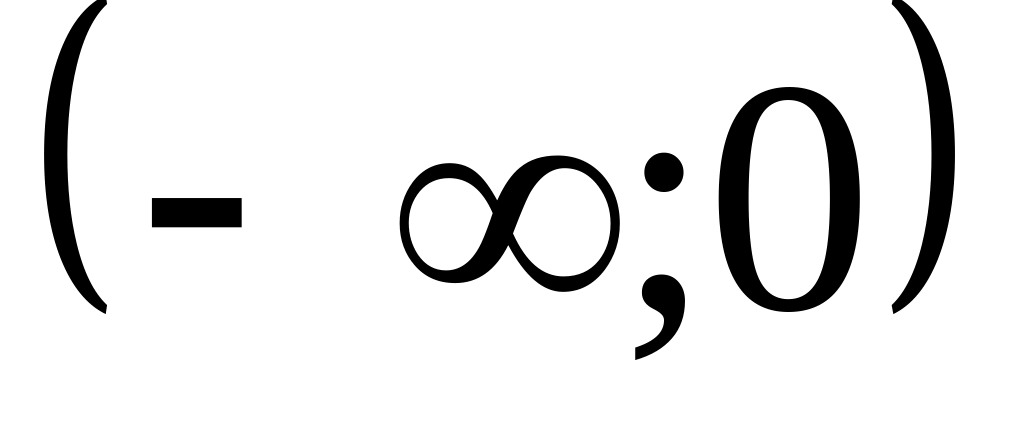
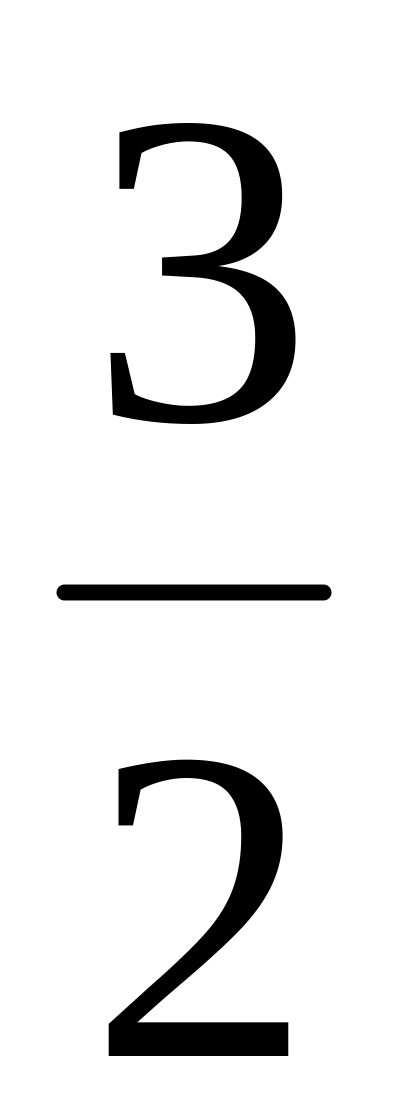
		нет экстр			min

Из таблицы находим интервалы монотонности функции: если функция убывает, если – функция возрастает. При .

5. Находим вторую производную

: ; , при любых значениях . Тогда решением является

				1
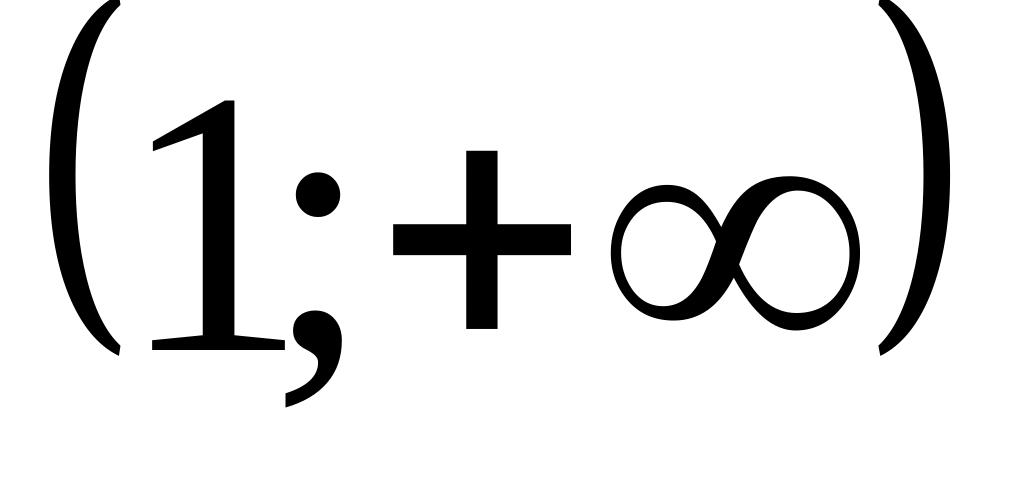
	+	перегиб		не существует	+
		0

График функции является вогнутым на интервалах и , выпуклым на интервале .

В точке функция имеет перегиб; .

6. Найдем асимптоты:

а) вертикальная ;

б) проверим наличие наклонных асимптот :

.

Отсюда следует, что наклонных асимптот нет.

7. График пересекает оси координат в точке . При .

Построим график (рис. 9).

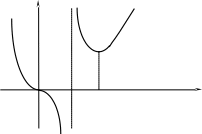
О 1 3/2

Рис. 9

4. Неопределенный интеграл