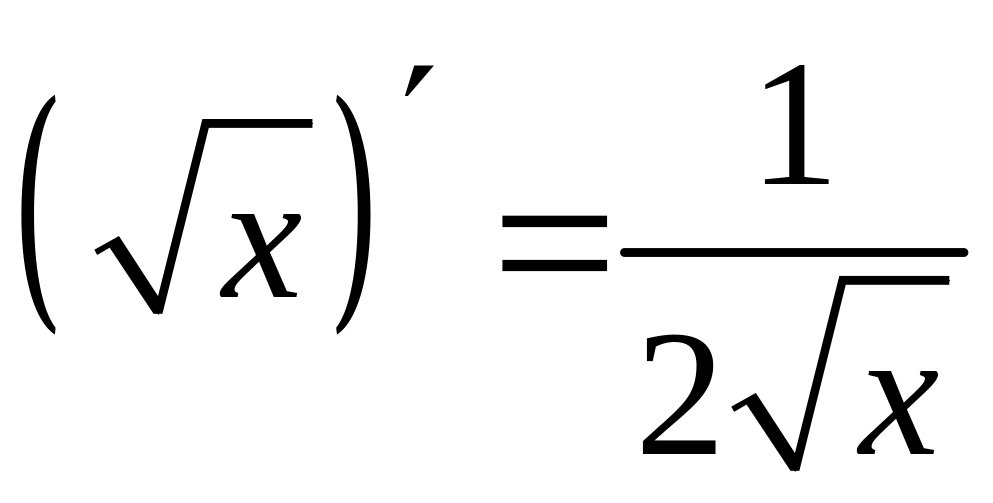- •Кафедра высшей и прикладной математики
- •1.1. Предел последовательности
- •1.2. Предел функции
- •Геометрическая интерпретация. Пусть дан график функции , имеющей предел при , равный (рис.2).
- •Бесконечно малые и бесконечно большие функции
- •Свойства пределов
- •1.3. Раскрытие неопределенностей
- •1.4. Первый замечательный предел
- •1.5. Второй замечательный предел
- •2.1. Понятие производной функции
- •Формулы дифференцирования
- •2.2. Производная сложной функции
- •Пример. Найти производную функции .
- •2.3. Дифференцирование неявной функции
- •Признаки возрастания и убывания функции
- •3.1. Экстремум функции
- •3.2. Точки перегиба График функции называется выпуклым на интервале , если он расположен ниже касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 а).
- •На интервале кривая выпукла , а на интервале – вогнута . Таким образом, при переходе через точку вторая производная меняет знак. Эта точка является точкой перегиба. Ее координаты .
- •3.3. Асимптоты
- •3.4. Общая схема исследования функции и построение ее графика
- •4.1. Первообразная функция и неопределенный интеграл
- •Основные свойства неопределенного интеграла
- •4.2. Непосредственное интегрирование
- •4.3. Интегрирование методом замены переменной (метод подстановки)
- •4.4. Интегрирование по частям
- •4.5. Интегрирование рациональных дробей
- •4.6. Интегрирование тригонометрических функций
- •5.1. Понятие определенного интеграла
- •Основные свойства определенного интеграла
- •5.2. Формула Ньютона-Лейбница
- •5.3. Методы интегрирования
- •7.1. Уравнение с разделяющимися переменными
- •7.2. Однородные дифференциальные уравнения первого порядка
- •7.3. Линейные дифференциальные уравнения
- •7.4. Дифференциальные уравнения второго порядка
- •7.5. Дифференциальные уравнения второго порядка с постоянными коэффициентами
- •8.1. Необходимый признак сходимости числового ряда
- •8.2. Достаточные признаки сходимости знакоположительных рядов
- •8.3. Знакочередующиеся ряды
- •Обобщенный признак Даламбера сходимости степенного ряда Для степенного ряда , где , составим предел модуля отношения последующего члена ряда к предыдущему
- •ЛиТература
1.4. Первый замечательный предел
Для
отыскание предела некоторых
тригонометрических функций применяется
правило: предел отношения синуса к
своему аргументу при
![]() равен единице
равен единице
![]() .
.
Часто
применяют формулу
![]() .
.
Пример. Найти
1)
![]() .
2)
.
2)
![]() .
.
Решение. На основании приведенного выше правила имеем:
1)
 .
.
2)
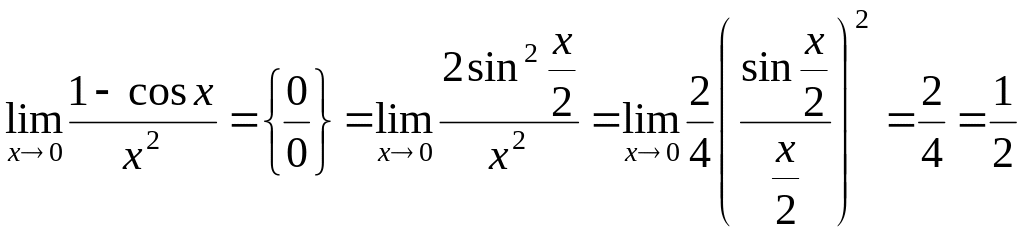 .
.
1.5. Второй замечательный предел
В
случае возникновения неопределенности
вида
![]() применяют второй замечательный предел:
применяют второй замечательный предел:

![]()
Число
![]()
![]() широко применяют в математике. В
частности, число
берут в качестве основания логарифма.
Такие логарифмы называют натуральными:
широко применяют в математике. В
частности, число
берут в качестве основания логарифма.
Такие логарифмы называют натуральными:
![]() .
.
Пример.
Вычислить
![]() .
.
Решение. Чтобы вычислить этот предел с помощью второго замечательного предела необходимо сначала выделить единицу
![]()
 .
.
2. Производная функции |
2.1. Понятие производной функции
Рассмотрим функцию
![]() .
На кривой
(рис. 3) возьмем произвольную точку
с
абсциссой
.
Придадим
приращение
.
На кривой
(рис. 3) возьмем произвольную точку
с
абсциссой
.
Придадим
приращение
![]() .
Новому значению
.
Новому значению
![]() соответствует точка
кривой. При этом функция получит
приращение
соответствует точка
кривой. При этом функция получит
приращение
![]() .
.
Рис. 3 |
Отношение
|
будет характеризовать
ту скорость, с которой меняется функция
в точке
.
Поэтому за мгновенную скорость изменения
функции в точке
![]() естественно принять
естественно принять
 .
.
Этот предел и называется производной.
Определение. |
Производной функции
|
Производная представляет собой скорость изменения функции в точке , т.е. скорость, с которой изменяется функция при переходе через точку. Таков наиболее общий смысл производной.
Геометрический смысл производной. Производная в точке равна тангенсу угла наклона касательной к кривой в точке , т.е. угловому коэффициенту касательной.
В теоретическом плане
подчеркнем, что существование предела,
которым выражается производная, надо
понимать в общем смысле существования
предела функции в точке. Это означает,
что
![]() должен существовать не только при
должен существовать не только при
![]() ,
но и при
,
но и при
![]() ,
причём оба предела должны совпадать. В
этом требовании и заключается условие
существования производной в точке
.
С геометрической точки зрения это
условие означает независимость
предельного положения секущей от выбора
точки справа или слева от точки
.
,
причём оба предела должны совпадать. В
этом требовании и заключается условие
существования производной в точке
.
С геометрической точки зрения это
условие означает независимость
предельного положения секущей от выбора
точки справа или слева от точки
.
Функция, имеющая производную, называется дифференцируемой.
Таблица производных