7.5. Дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейным однородным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
где
и
– постоянные величины.
Для нахождения общего решения однородного уравнения составляется характеристическое уравнение
.
Структура общего решения однородного уравнения зависит от характера корней:
если корни вещественные, различные, т.е.
,
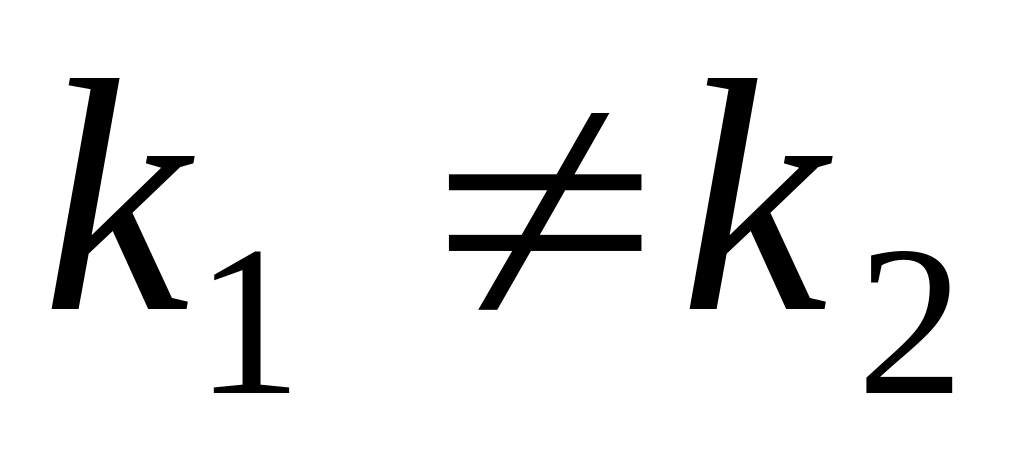то общее решение уравнения имеет вид:
если корни вещественные, кратные, т.е.
,
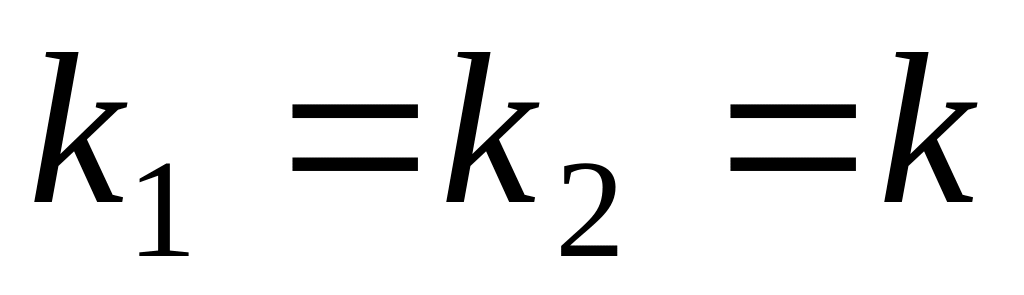то общее решение уравнения имеет вид:
если корни комплексные, т.е.
,
то общее решение уравнения имеет вид
Пример.
Решить уравнение
.
Решение.
Ему соответствует характеристическое
уравнение
,
корнями которого являются
.
Следовательно, общее решение однородного
уравнения имеет вид
.
Пример.
Решить уравнение
.
Решение.
Ему соответствует характеристическое
уравнение
.
Найдем его корни:
.
Корни вещественные
кратные, т.е.
,
Следовательно, общее решение уравнения
имеет вид:
.
Пример.
Решить уравнение
.
Решение.
Ему соответствует характеристическое
уравнение
.
Найдем его корни:
.
Действительная часть
,
мнимая часть
.
Следовательно, общее решение однородного
уравнения имеет вид
.
8. Числовые ряды |
Рядом называется сумма бесконечного множества слагаемых
являющихся членами бесконечной последовательности.
Числа
называются членами ряда.
Сумма первых членов ряда называется -ой частичной суммой.
.
Ряд называется
сходящимся, если последовательность
его частичных сумм при
имеет конечный предел:
Этот предел называется суммой сходящегося ряда.
Если
не существует или бесконечен, то ряд
называется расходящимся.
Пример. Написать -ый член ряда по данным первым его членам.
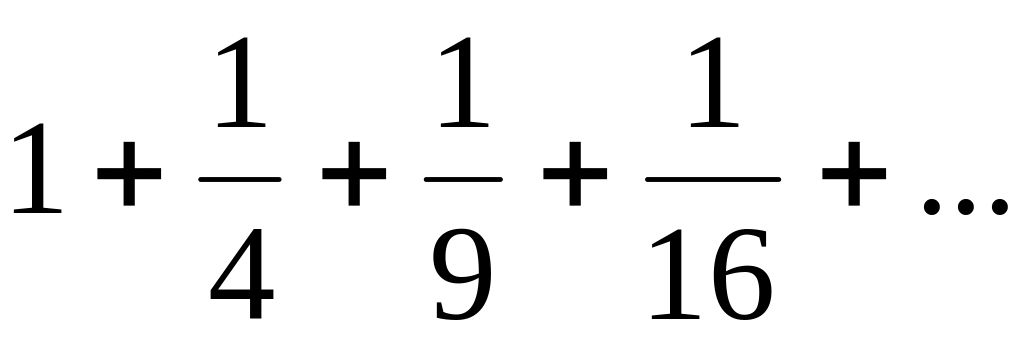Ответ:
.
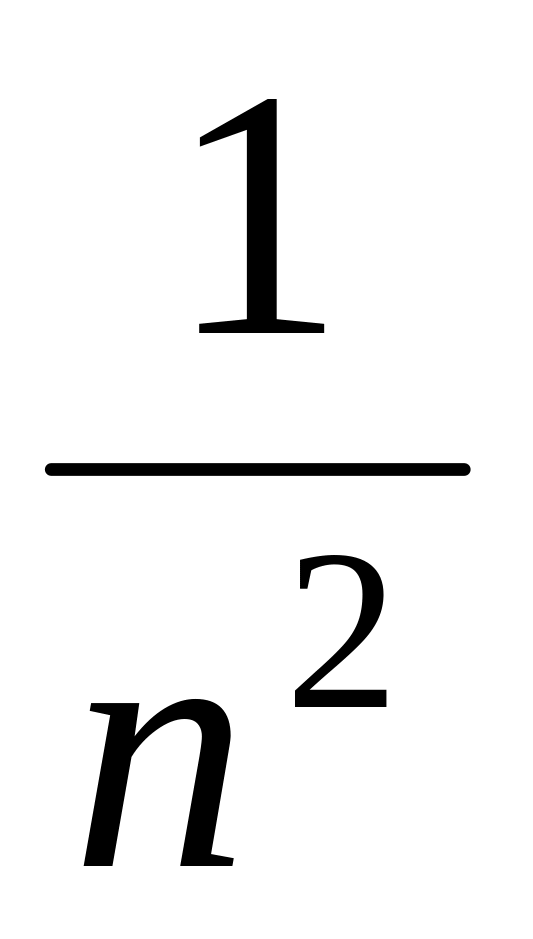Ответ:
.
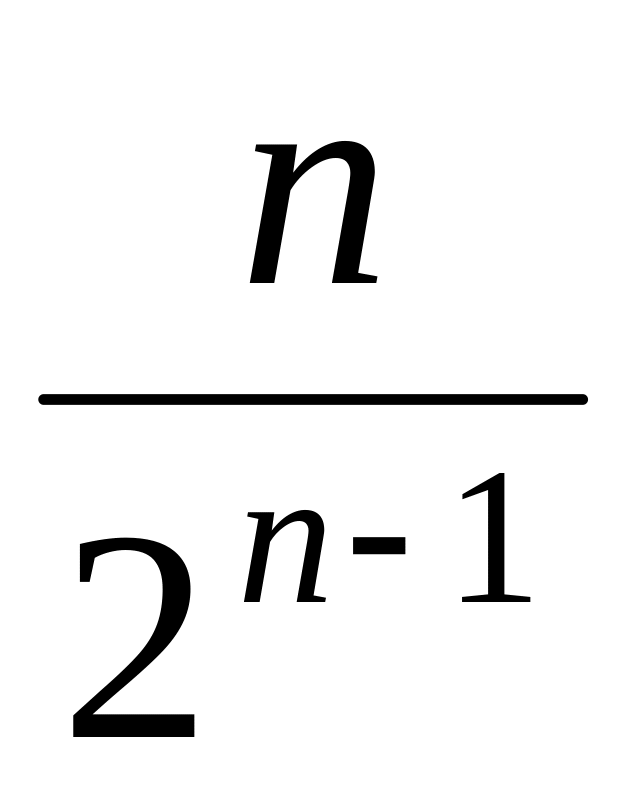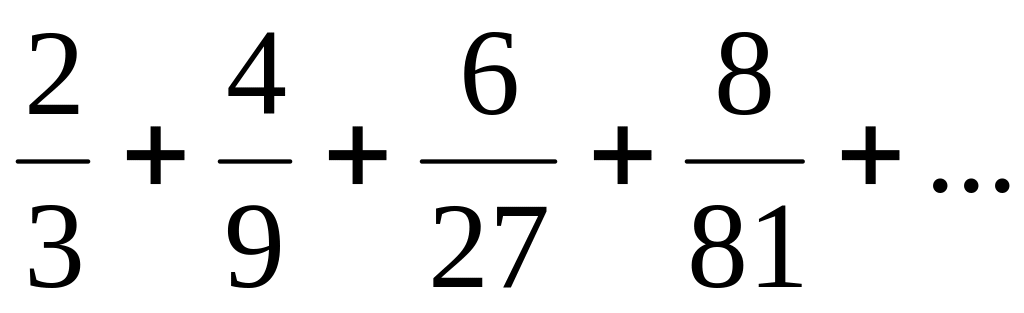Ответ:
.
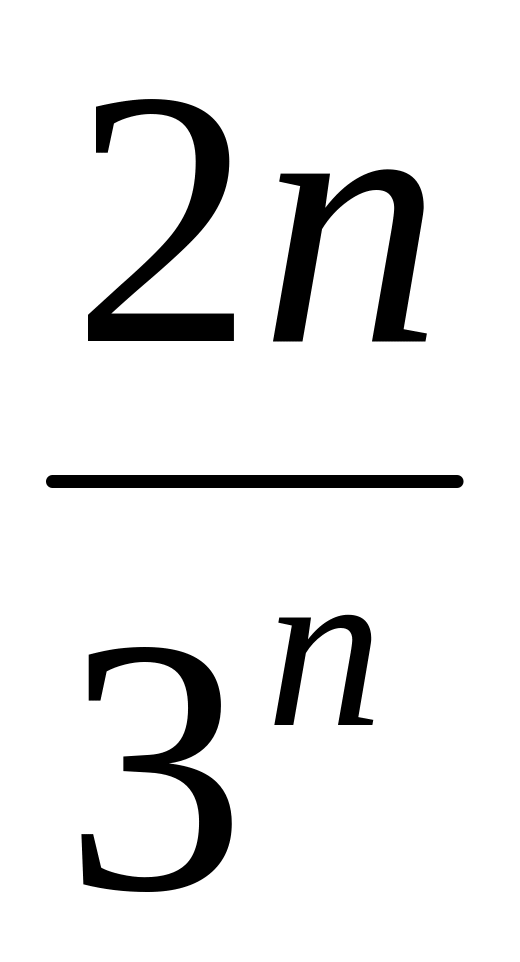8.1. Необходимый признак сходимости числового ряда
Если ряд
сходится, то его общий член
при
,
т.е.
.
! Этот общий признак не является достаточным, т.е. из того, что общий член стремиться к нулю при , нельзя сделать вывод о сходимости ряда. Но если общий член не стремится к нулю, то ряд расходится.
Пример.
Исследовать на сходимость ряд
Решение.
Проверим, выполняется ли необходимое
условие сходимости ряда, а именно
.
В наше случае
,
тогда
.
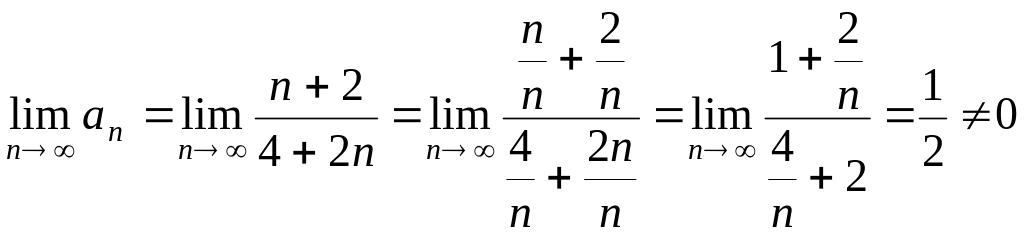Так как необходимое условие не выполняется, то этот ряд расходится.
Ряд, членами которого являются только положительные числа, называется знакоположительным.
8.2. Достаточные признаки сходимости знакоположительных рядов
Признак Даламбера. |
Если для положительного
ряда существует
|
,
то
при
ряд сходится,
при
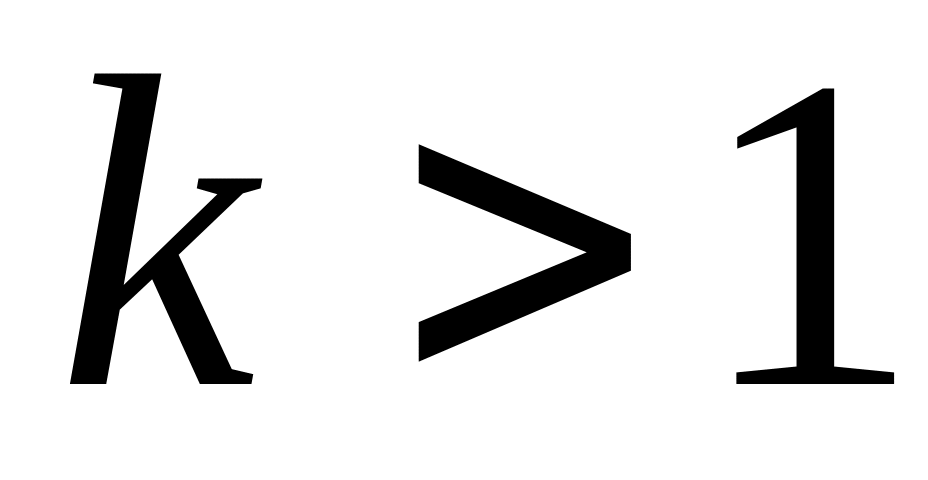ряд расходится,
при
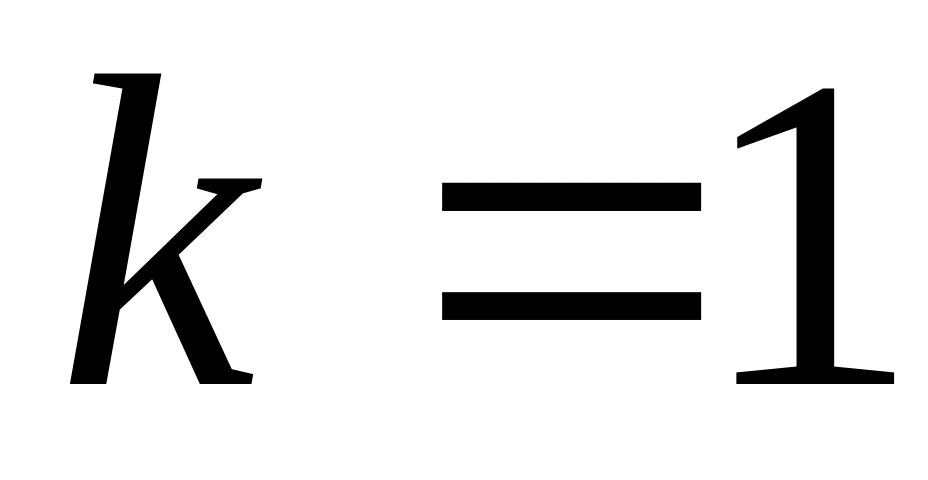о сходимости ряда сказать ничего нельзя,
т.е. надо применять другой признак.
Пример. Исследовать на сходимость ряд
Решение.
Находим
,
.
– ряд сходится.
Интегральный признак Коши. |
Ряд с положительными
членами
|
сходится или расходится одновременно
с несобственным интегралом
,
где – непрерывная, положительная, монотонная убывающая производящая функция.
Пример.
Исследовать
на сходимость гарнмонический ряд
.
Решение. Вычислим
.
Гармонический ряд расходится.
Пример. Исследовать на сходимость ряд
Решение.
Члены ряда можно рассматривать как
значения функции
при
Члены ряда убывают:
Вычислим
.
Несобственный интеграл сходится, значит сходится и данный ряд.
Радикальный признак Коши. |
Если для положительного
ряда существует
|
,
то
при ряд сходится,
при ряд расходится,
при о сходимости ряда сказать ничего нельзя.
(Этот признак применяется
лишь тогда, когда
извлекается).
Пример.
Исследовать на сходимость
Решение. Преобразуем выражение под знаком суммы.
Применяя радикальный признак Коши, имеем:
Таким образом, исходный ряд сходится.
Первый признак сравнения. |
Сравним ряд с положительными членами
с другим знакоположительным рядом
|
если ряд
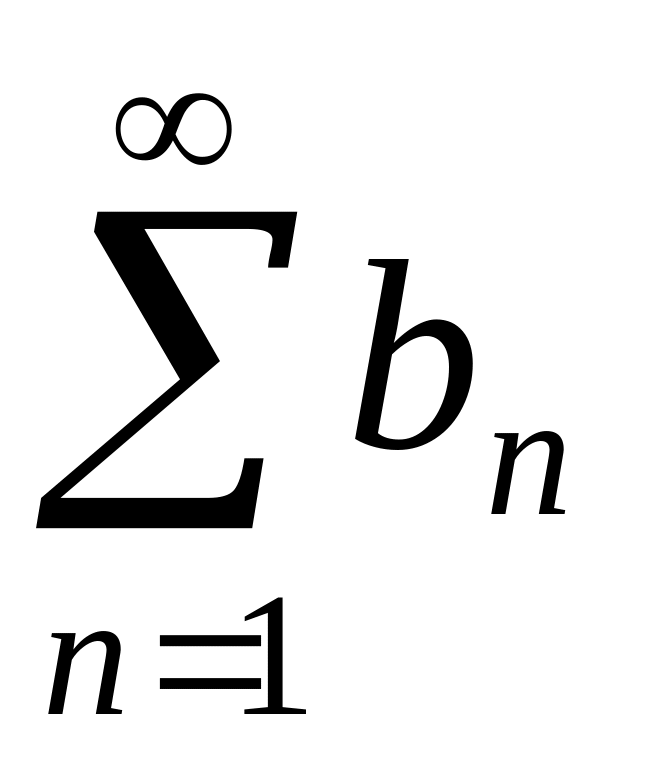сходится и начиная с некоторого члена
ряда выполняется неравенство
,
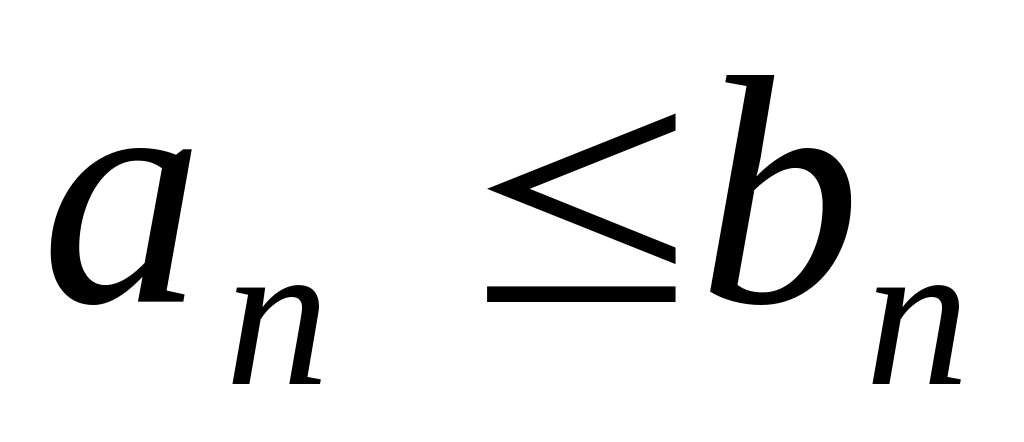то ряд
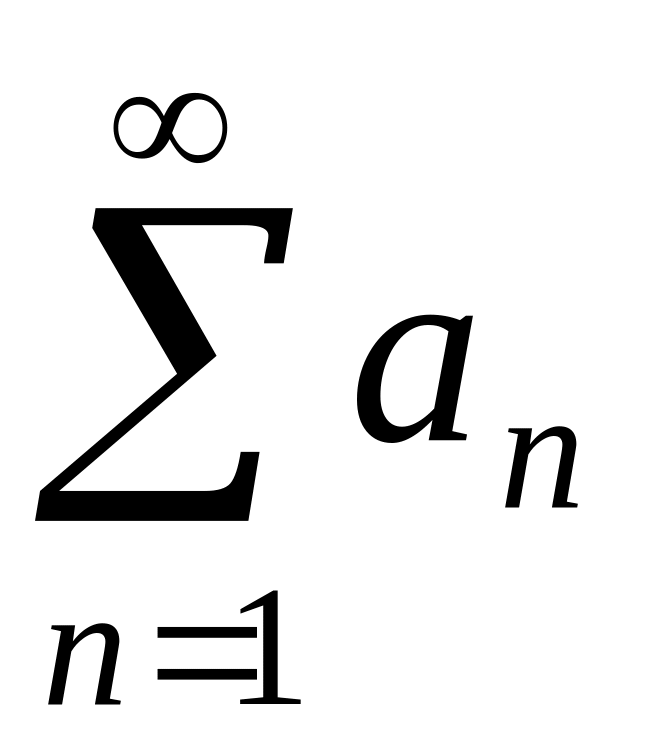также сходится;если ряд расходится и начиная с некоторого члена ряда выполняется неравенство
,
то и ряд
также расходится.
Пример. Исследовать
сходимость ряда
Решение. Сравним данный ряд с гармоническим рядом
Т.к. каждый член исходного ряда, начиная со второго, больше соответствующего члена гармонического ряда, а гармонический ряд является расходящимся (интегральный признак), то данный ряд тоже расходится.
Замечание.
Обобщенный гармонический ряд
при
сходится, при
расходится.
Второй признак сравнения. |
Даны два положительных ряда и . Если существует конечный предел отношения членов ряда при , отличный от нуля, то оба ряда сходятся, либо расходятся одновременно, т.е.
|
и
.
Пример.
Исследовать ряд на сходимость
.
Решение.
Сравним этот ряд со сходящимся рядом
(он сходится по интегральному признаку).
Проверим, существует конечный, отличный
от нуля предел
.
Таким образом, ряд является сходящимся.