4.6. Интегрирование тригонометрических функций

1. Интегралы вида , где 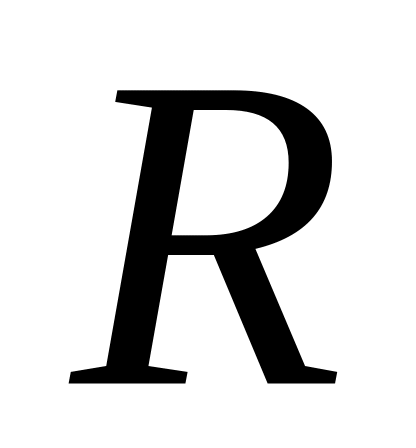- рациональная функция.

Интегралы указанного вида приводятся к интегралам от рациональных функций с помощью универсальной тригонометрической подстановки: . В результате этой подстановки имеем:

.

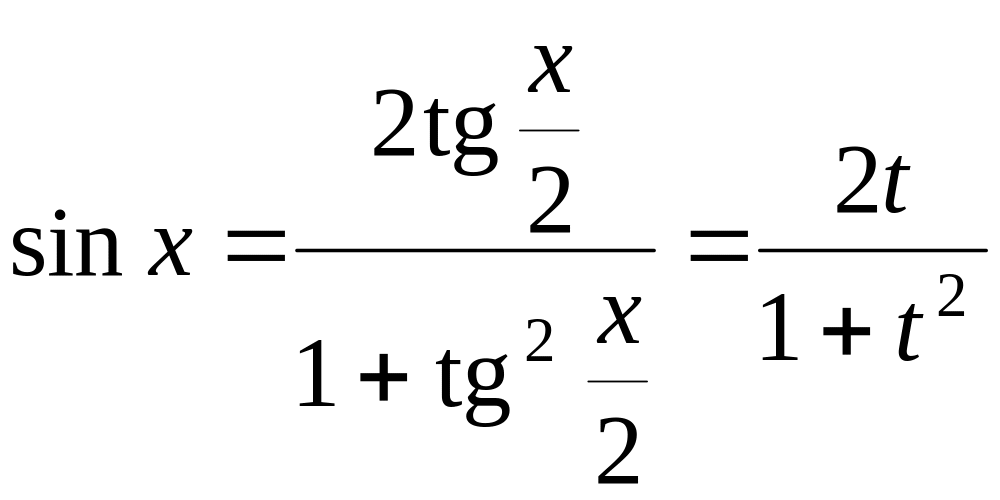
Пример. Найти интеграл .

Решение. Подынтегральная функция рационально зависит от и : применяем подстановку , тогда , , .

.

Возвращаясь к старой переменной, получаем:

.

2. Интегралы вида .

Выделим два случая, имеющие особенно важное значение.

Случай 1.

По крайней мере один из показателей или – положительное нечетное число.

• если – нечетное положительное число, то применяется подстановка ;

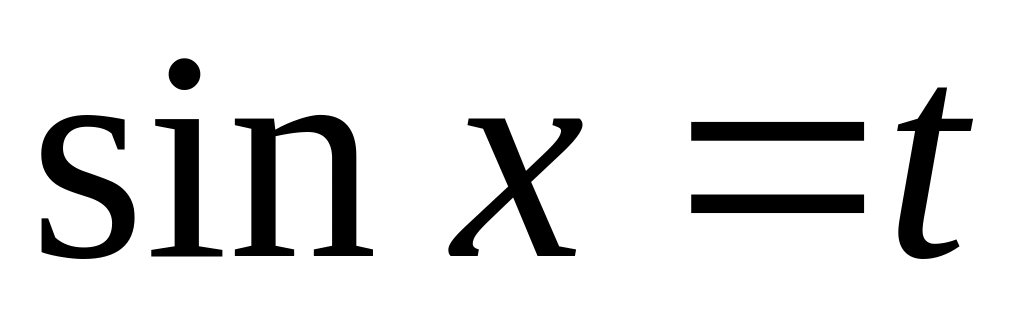• если – нечетное положительное число, то применяется подстановка .

• если и оба нечетные и 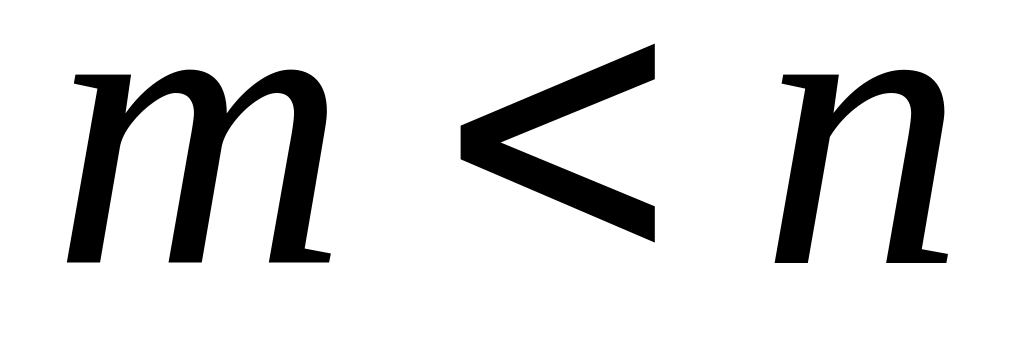, то применяется подстановка ;

• если и оба нечетные и , то применяется подстановка ;

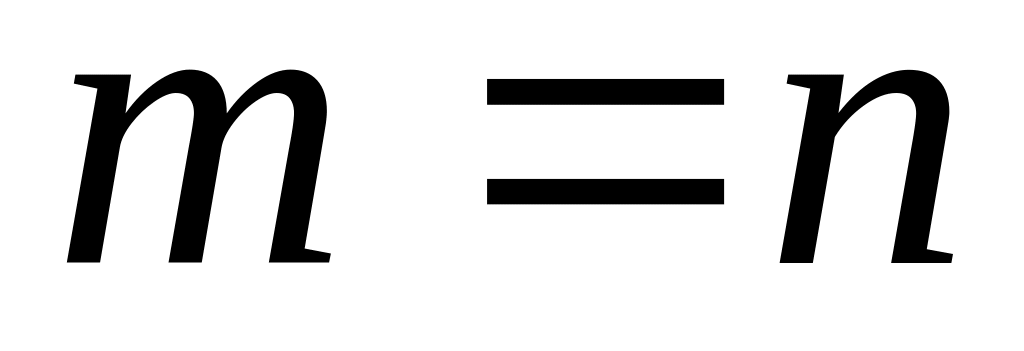• если и оба нечетные и , то применяют любую из подстановок или ;

Пример. Найти интеграл .

Решение. Здесь , , значит применяем подстановку , откуда . Далее имеем:

.

Случай 2.

Оба показателя степени и – четные положительные числа.

Здесь следует преобразовать подынтегральную функцию с помощью формул:

Пример. Найти интеграл .

Решение. Применяем последовательно первую и вторую из этих формул:

.

Итак,

.

3. Интегралы вида ; ; .

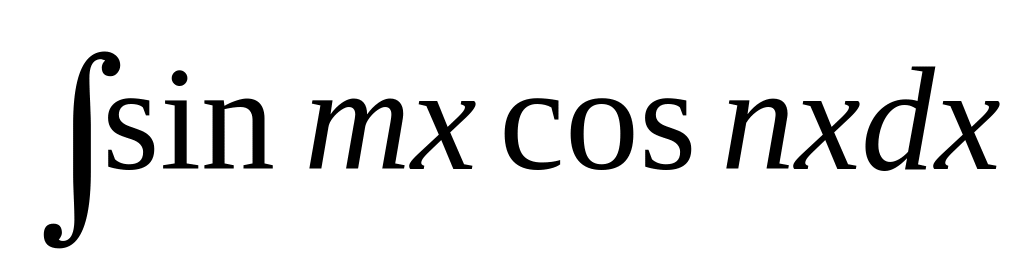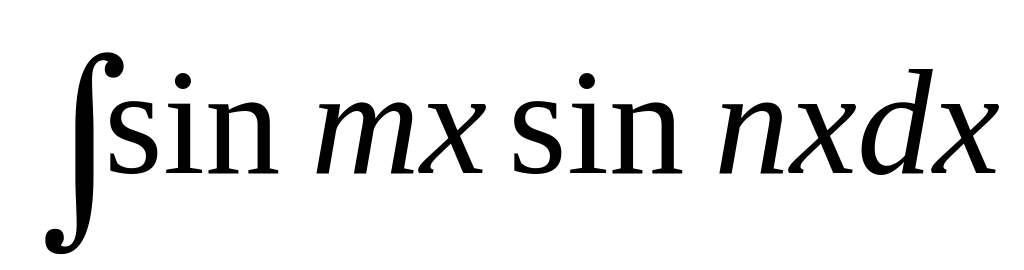Тригонометрические формулы:

дают возможность произведение тригонометрических функций предоставить в виде суммы.

Пример. Найти интеграл .

Решение. Используя первую формулу, получим

.

5. Определенный интеграл

5.1. Понятие определенного интеграла

Пусть функция определена и непрерывна на отрезке . Разделим отрезок на произвольных частей точками , выберем на каждом элементарном отрезке произвольную точку и найдем длину каждого такого отрезка: .

Интегральной суммой для функции на отрезке называется сумма вида

.

Для каждой непрерывной на функции можно построить бесконечное число интегральных сумм, каждая из которых зависит от разбиения отрезка на части и выбора точек на каждом элементарном отрезке.

Определение.

Определенным интегралом от функции на отрезке называется предел интегральных сумм при условии, что длина наибольшего из элементарных отрезков стремится к нулю; если этот предел существует и не зависит от способа разбиения отрезка на части и выбора точек на каждом из элементарных отрезков:

.

Числа и называют пределами интегрирования; – отрезком интегрирования; – подынтегральной функцией; – подынтегральным выражением; – переменной интегрирования.

Теорема

существования определенного интеграла. Если функция непрерывна на , то предел интегральной суммы существует и не зависит от способа разбиения отрезка на элементарные и от способа выбора точек .

Если на , то определенный интеграл геометрически представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями (рис. 10).

	0
Рис. 10