Порядок расчет первого задания.

1) Рассчитать параметры , , , , и с помощью выражений 3.3-3.5.

2) Рассчитать требуемый минимальный порядок фильтра согласно выражениям 3.21, 3.23 для всех видов аппроксимации Баттерворта, Чебышева первого рода и Чебышева второго рода и занести результаты расчета в следующую таблицу:

Таблица 3.2

Параметры коридора АЧХ						Требуемый порядок фильтра
						Баттерворта	Чебышева

3) Провести анализ результатов расчета, предствленных в таблице и обосновать выбор типа аппроксимации.

4) Рассчитать комплексную передаточную функцию фильтра, используя выражения 3.13, 3.15, 3.17.

5) Построить АЧХ и ФЧХ рассчитанного аналогового фильтра нижних частот.

6) Построить АЧХ и ФЧХ фильтра с использованием встроенных функций Matlab.

7) Провести сравнение и анализ полученных результатов.

4. Порядок выполнения задания №2. Расчет цифрового фильтра методом частотной выборки с использованием окон.

В данной задании неоходимо рассмотреть порядок расчета КИХ фильтра по заданной амплитудно-частотной характеристике (АЧХ) с линейной ФЧХ методом частотной выборки с использованием окон.

Для КИХ фильтров – количество коэффициентов импульсной характеристики на единицу больше чем порядок фильтра . Напомним, что порядок фильтра всегда равен количеству линий задержки структурной схемы КИХ фильтра, показанной на рисунке 4.1.

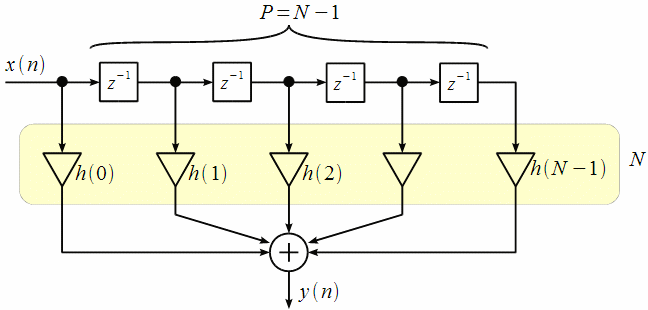
Рисунок 4.1. Структурная схема КИХ фильтра

Коэффициенты КИХ фильтра равны значениям отсчетов импульсной характеристики . Таким образом, фильтры четного порядка содержат нечетное количество коэффициентов, а фильтры нечетного порядка — четное.

Обозначим 4 типа импульсных характеристик КИХ фильтра, обладающих линейной ФЧХ как это показано на рисунке 4.2.

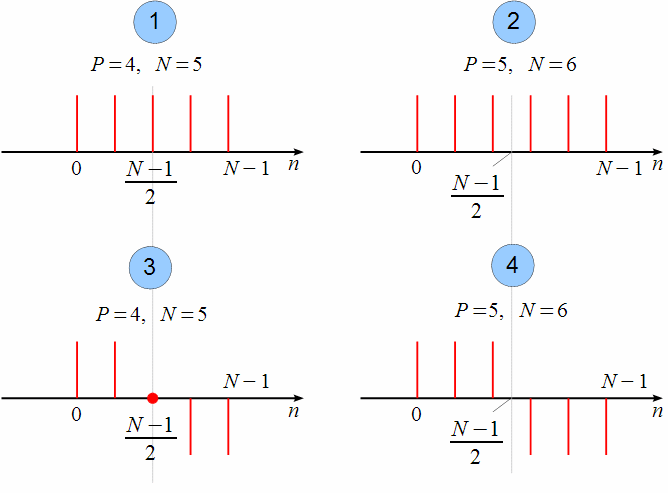Рисунок 4.2. Типы импульсных характеристик КИХ фильтров

с линейной ФЧХ

Фильтр 1-го типа. Фильтр четного порядка с нечетным количеством коэффициентов . Импульсная характеристика симметрична относительно отсчета , т. е. , , при этом ось симметрии попадает на данный отсчет.

Фильтр 2-го типа. Фильтр нечетного порядка с четным количеством коэффициентов . Импульсная характеристика симметрична относительно оси симметрии , т. е. , .

Фильтр 3-го типа. Фильтр четного порядка с нечетным количеством коэффициентов . Импульсная характеристика антисимметрична относительно отсчета , т. е. , при этом ось симметрии попадает на центральный отсчет, который должен быть равен нулю .

Фильтр 4-го типа. Фильтр нечетного порядка с четным количеством коэффициентов . Импульсная характеристика антисимметрична относительно оси симметрии , т. е. .

Пусть задана АЧХ КИХ фильтра аналитически, или предварительно измеренная каким-либо способом. АЧХ КИХ фильтра — периодическая, четная функция с периодом рад/c, как это показано на рисунке 4.3.

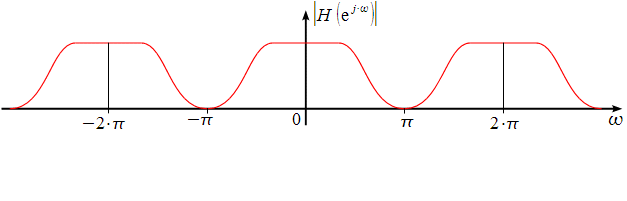
Рисунок 4.3. Периодическая симметричная АЧХ КИХ фильтра

Частота цифрового фильтра всегда нормирована к частоте дискретизации, поэтому все частотные характеристики фильтров задаются на интервале от 0 до рад/c.

Если бы у нас был комплексный коэффициент передачи фильтра (без модуля), то мы могли бы произвести расчет импульсной характеристики как разложение в ряд Фурье периодической функции :

(4.1)

Но у нас задана только АЧХ, т.е. модуль комплексного коэффициента передачи , поэтому мы должны добавить ФЧХ , тогда:

. (4.2)

Таким образом, мы должны к требуемой АЧХ задать линейную ФЧХ и рассчитать КИХ согласно (4.2). Для того чтобы правильно задать линейную ФЧХ мы должны потребовать, чтобы фильтр вносил постоянную групповую задержку для любого из четырех типов фильтров. Тогда

. (4.3)

При расчете неопределенного интеграла постоянная интегрирования приравнена к нулю.

Окончательно выражение для импульсной характеристики КИХ фильтра с линейной ФЧХ принимает вид:

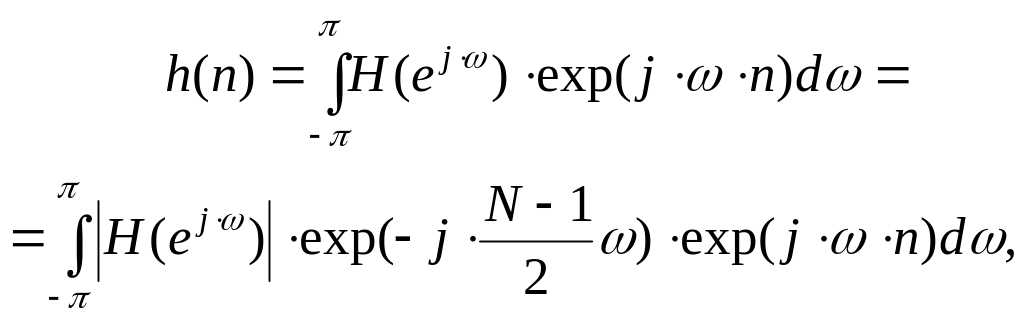(4.4)

Данное выражение позволяет произвести аналитический расчет импульсной характеристики КИХ фильтра с линейной ФЧХ. Однако, на практике АЧХ может не быть задана аналитически, а даже если и задана, то аналитическое интегрирование не всегда возможно.

Численный расчет КИХ фильтра производится на основе обратного дискретного преобразования Фурье (ОДПФ).

Для этой цели мы можем продискретизировать комплексный коэффициент передачи КИХ фильтра как это показано на рисунке 4.4 и рисунке 4.5 для четного и нечетного количества коэффициентов КИХ фильтра соответственно.

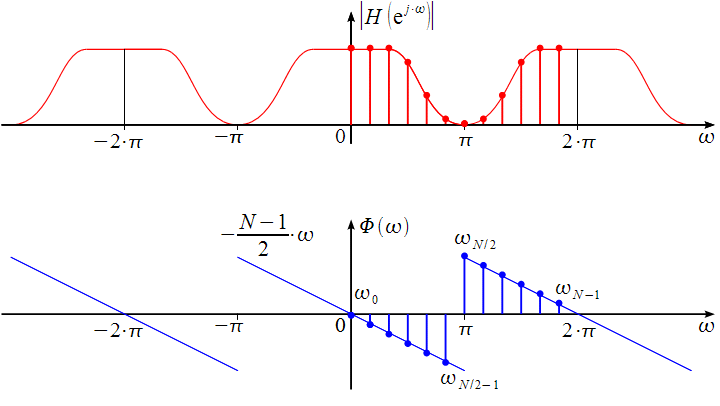Рисунок 4.4. Дискретизация периодической АЧХ и ФЧХ КИХ фильтра при четном N

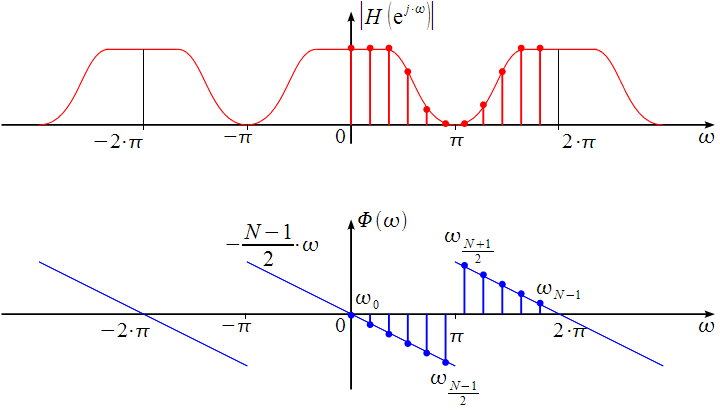Рисунок 4.5. Дискретизация периодической АЧХ и ФЧХ КИХ фильтра при нечетном N

Дискретизацию будем осуществлять на равноотстоящей сетке:

(4.5)

Тогда АЧХ и ФЧХ дискретизируются на данной сетке частот и комплексный коэффициент передачи представляется дискретными отсчетами:

(4.6)

где – дельта-функция:

(4.7)

Подставив выражение (4.6) в (4.4) получим:

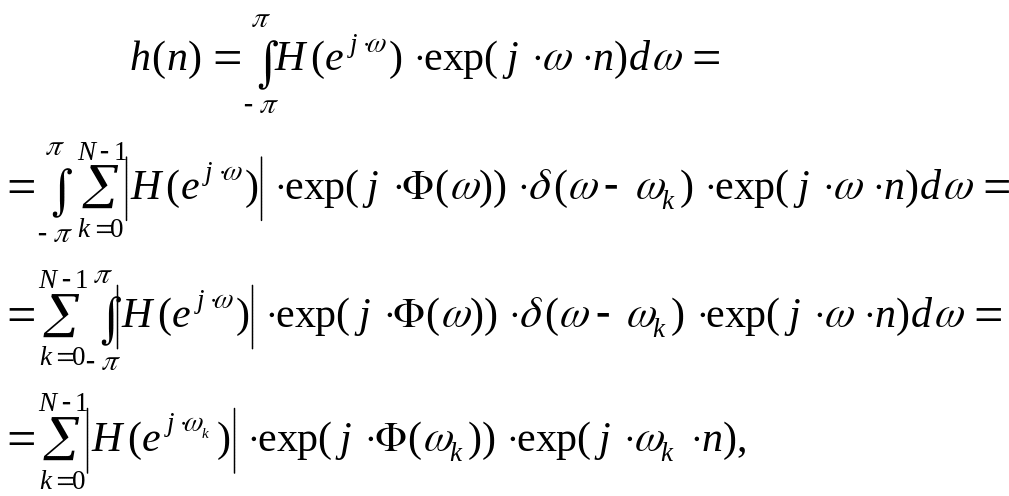(4.8)

В выражении (4.8) операции интегрирования и суммирования поменяны местами и применено фильтрующее свойство дельта-функции.

Учтем (4.5) и окончательно можно записать:

(4.9)

Выражение (4.9) ничто иное, как обратное дискретное преобразование Фурье (ОДПФ) комплексного коэффициента передачи

(4.10)

Это позволяет производить численный расчет КИХ фильтра с произвольной АЧХ с применением алгоритмов быстрого преобразования Фурье, что существенно увеличивает эффективность данного метода.

При расчете необходимо правильно дискретизировать ФЧХ комплексного коэффициента передачи, так как это показано на рисунках 4.3 и 4.5. Так для фильтра с четным количеством коэффициентов ФЧХ дискретизируется согласно выражению (рисунок 4.3):

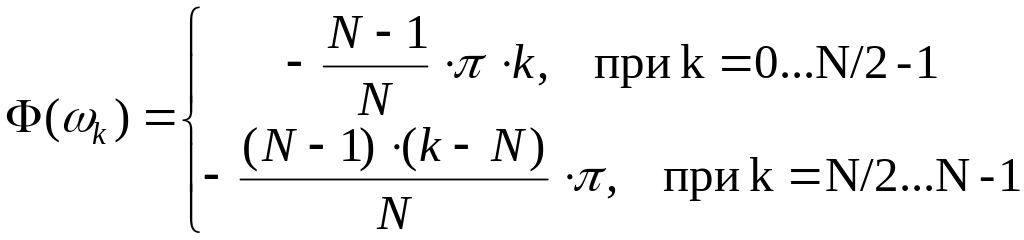(4.11)

В случае нечетного количества коэффициентов КИХ фильтра , ФЧХ дискредитируется согласно выражению (рисунок 4.5):

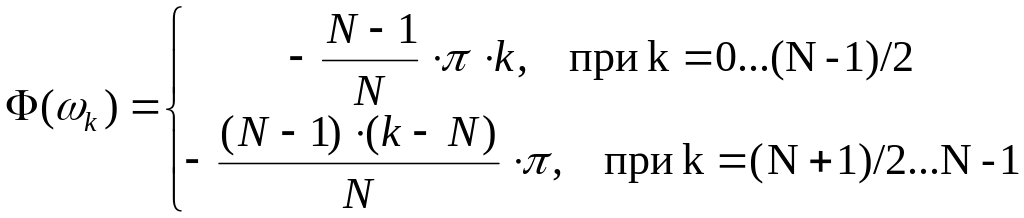(4.12)

В случае четного мы получим КИХ фильтр 2-го или 4-го типа, а при нечетном – первого или третьего типа.

Такая дискретизация ФЧХ необходима, чтобы обеспечить свойства симметрии комплексного коэффициента передачи фильтра, который по сути – дискретное преобразование Фурье от импульсной характеристики КИХ фильтра. Поскольку импульсная характеристика должна быть чисто вещественной, то необходимо выдерживать симметрию АЧХ и ФЧХ, иначе при расчете импульсной характеристики при помощи ОДПФ появится мнимая часть.

Основное достоинство метода частотной выборки заключается в том, что он позволяет довольно просто рассчитать КИХ фильтр с линейной ФЧХ и произвольной АЧХ, заданной на сетке частот . Для этого требуется построить комплексный коэффициент передачи фильтра на заданной сетке частот, и взять от него обратное дискретное преобразование Фурье. Однако при всей простоте данного метода, он хранит в себе недостатики.

При усечении импульсной характеристики наблюдается сильная неравномерность АЧХ в полосе пропускания фильтра, и высокий уровень боковых лепестков в полосе заграждения.

Данный эффект носит название эффекта Гиббса и возникает ввиду ограничения количества отсчетов импульсной характеристики.

Физический смысл эффекта Гиббса заключается в следующем: при дискретизации АЧХ мы задаем точки через которые должна пройти АЧХ рассчитанного фильтра, однако мы не накладываем никаких ограничений на поведение АЧХ в других точках. При расчете мы получаем набор коэффициентов КИХ фильтра как разложение в ряд Фурье комплексного коэффициента передачи. Эти коэффициенты разложение мы рассчитываем через обратное дискретное преобразование Фурье. Поскольку мы ограничиваем количество коэффициентов разложения (количество коэффициентов КИХ фильтра), то получаем усеченный ряд, который лишь аппроксимирует идеальную АЧХ. Аппроксимация будет тем лучше, чем больше коэффициентов импульсной характеристики, т. е. чем чаще мы будем дискретизировать идеальную АЧХ. Эффект Гиббса – негативный эффект, который не позволяет получить КИХ фильтр высокой избирательности. Поэтому было предложено использовать для расчета КИХ фильтров аппарат весовых окон, которые были рассмотрены при спектральном анализе ограниченных во времени сигналов. Использование весовых окно позволяет улучшить частотные характеристики КИХ фильтров.

С целью уменьшения эффекта Гиббса необходимо умножить полученную импульсную характеристику на оконную весовую функцию :

(4.13)