Устойчивость и качеств линейных сар.

1. Понятие об устойчивости линейных систем.

Устойчивость - свойство САР возвращаться в исходный или близкий к нему установившейся режим, после выхода из него в результате какого-либо воздействия.

Не устойчивая работа может возникать в любой САР с обратной связью в результате чего система не возвращаться в состояние равновесия или колеблется вокруг него с недопустимой амплитудой. Об устойчивости системы можно судить из решения линеаризованного ДУ замкнутой системы:

a(p)y(t)=b(p)g(t)+r(p)f(t) (1)

Из уравнения 1:

y(t)=yпер(t)+yуст(t)

Общее решение ОДУ a(p)y(t)=0 (2) определяет yпер(t). Составляющая yуст(t) находится как часное решение неоднородного уравнения (1)0.

САР называется устойчивой, если переходная составляющая со временем затухает, то есть .

Если же , то система называется не устойчивой.

Системы в которых переходный процесс с течением времени не расходится и не затухает называется находящимся на границе устойчивости.

Чтобы исследовать систему на устойчивость нет необходимости решение уравнения (2), так как оно зависит от характеристических корней уравнения: a(s)=0.Обозначим через S1,S2, …, Sn корни характеристического полинома: (3). Тогда переходный процесс ,

где Ck-произвольная постоянная.

Следовательно (4)

Корни характеристического уравнения 3 могут быть вещественными

Sk=ακ, или комплексно-сопряженными , где ακ=ReSk, βκ=ImSk.

Тогда: (5)

Из двух последних уравнений (4) и (5) следует необходимые и достаточные условия устойчивости линейной системы

Для того чтобы линейная система была устойчивой необходимо, чтобы вещественные части корней характеристического уравнения 3 были отрицательными (т.е. ReSk<0, k=1, n).

Если рассматривать комплексную плоскость, то корни характеристического уравнения устойчивой системы будет располагаться в левой полуплоскости (II

и III четверть).

Система находится на апериодической границе устойчивости, если имеется

хотя бы один ненулевой

корень.

Система находится на колебательной границе устойчивости, если имеется хотя бы одна пара чисто линейных корней. В этом в системе возникают незатухающие колебания.

С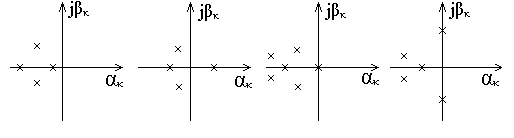 истема становится неустойчивой, если бы один корень находится в правой плоскости.

Прямой путь определения устойчивости системы, состоящей в нахождении корней характеристического уравнения, весьма трудоемок, если n>3-4-x.

Поэтому для исследования сложной системы используется другие методы, называемыми критериями устойчивости.

2. КРИТЕРИИ УСТОЙЧИВОСТИ РАУСА-ГУРВИЦА.

   Этот критерий относится к алгебраическим критериям устойчивости. Он накладывает ограничение на коэффициенты характеристического уравнения (3) (предведущий параграф).

Если характеристическое уравнение системы имеет вид (3), причем a0>0, то для устойчивости САР необходимо и достаточно, чтобы были положительными n определителей Гурвица: Δ1,Δ2,Δ3,…,Δn .

Определители Гурвица т.Е. Диагональные определители квадратной матрицы вида:

ai- коэффициенты характеристического

у равнения 3

Последний определитель Δn можно выразить следующим образом:

Δn=anΔn-1 . Поэтому вычислять его не требуется, а условие Δn>0 будет выполнятся при Δn-1=0, an=0 и когда Δn-1>0, an=0.

Условия, при котором система находится на границе устойчивости, можно получить при Δn=0 и неотрицательности всех других определителей. При этом возможны две ситуации: когда Δn-1=0, an>0 и когда Δn-1>0, an=0.

Условие Δn-1=0 соответствует колебательной границе устойчивости, а условие an=0 соответствует аперидической границе устойчивости.

Критерий устойчивости Рауса-Гурвица рационально применять для уровнений 4-5 порядка. Сформулируем условие устойчивости на основании этого критерия для систем различного порядка.