Математическое описание систем автоматического управления и регулирования. Элементы и звенья сау.

Известно, что любая система АР или САУ может рассматриваться в виде совокупностей элементов, соответствующим образом связанных между собой.

Такой подход позволяет ввести понятия функциональной схемы САР, что приносит пользу при рассмотрении принципов действия автоматических систем.

Для математического описания работы автоматической системы удобно разбивать их не на элементы, а на динамические звенья или просто звенья.

Динамическим звеном называется часть системы управления, описываемая дифференциально или иным уравнением определенного вида. Звено в отличии от элемента, не должно обязательно быть законченным конструктивно . Звено может быть отдельной частью элемента автоматически или объекта регулирования, в отдельных случаях звенья могут вообще не иметь физического смысла.

Ч тобы охарактеризовать состояние звена выбирают одну координату на входе и одну координату на выходе. Называют их соответственно входной x₁(t) и выходной x₂(t) величинами звена. Условное обозначение динамического звена следующее:

Зависимость x₂(x₁) в установившемся режиме называется статической характеристикой звена. Она обычно изображается графически в плоскости координат x₁ и x₂ и получается экспериментальным или расчетным путем.

В случае если x2 зависит также и от f, то получается семейство статических характеристик. Эти характеристики полностью описывают поведение звена в установившемся режиме. Для изучения поведения звена в переходном режиме, возникает необходимость нахождения решения дифференциального уравнения описывающего работу звена. Для звеньев непрерывного действия в общем, виде такое уравнение следующее:

F ( x₂⁽ⁿ⁾, x₂^(n-1), …, x₂, x₂, x₁^(m),x₁^(m-1), …,x₁,x₁,f^(g),f^(g-1),..,f,f )=0 (1)

Здесь n,m,g - натуральные числа, определяющие наивысший порядок производной от x2, x1, f.

F - функции от n+m+g+3 аргумент.

На практике обычно n>m; n>g поэтому число n называется порядком дифференциального уравнения при n=1 дифференциальное уравнение 1 имеет вид:

F ( x₂,x₂,x₁,f ) = 0 (2)

при n=2

F ( x₂,x₂,x₂,x₁,x,f,f, ) =0 (3)

Неизвестной в (1) является выходная величина x₂. Для решения уравнения (1) должны быть заданы величины x₁ и fn как функции времени и начальные условия.

Положив в (1) x₂=const , x₁=const, f=const можно получить статическую характеристику звена.

F ( 0, 0, …,0,x₂,00, … ,0,x₁,00, … ,0,f )=0

меняя x₁,x₂ можно получить семейство характеристик.

Линеаризация нелинейных уравнений динамических звеньев.

В случае когда (1) представляет собой нелинейную функцию своих аргументов динамика работы звено а описывается нелинейным дифференциальным уравнением, а само звено называется нелинейным звеном.

Исследование нелинейных дифференциальных уравнений существенно сложнее чем линейных, поэтому всегда когда это возможно стремиться линеаризовать нелинейное дифференциальное уравнение, то есть , найти такое линейное дифференциальное уравнение решение которого достаточно близко к нелинейному. Так как большинство элементов САР являются нелинейными, то задача линеаризации имеет широкое распространение.

Простейшей способ линеаризации основан на простейшем разложении функции в ряд Тейлора, с последующим отбрасыванием нелинейных членов разложения.

Рассмотрим этот способ применительно к уравнению (2), имеющему I порядок. Все изложенное будет справедливо и для уравнений более высокого порядка.

Линеаризация производиться относительно некоторого заранее выбранного режима работы звена. Чаше всего выбирается установившийся режим. Он характеризуется постоянством всех координат. Для (2) уравнение исходного режима можно представить следующим образом: x1=x10, x2=x20, f= f0, x2=0

где x₁⁰, x₂⁰, f⁰ - постоянные величины, связанные между собой соотношением: F ( 0,x₂⁰,x⁰,f⁰)=0

Выбрав исходный режим, далее, для линеаризации поступают следующим образом.

1 Представляют все входящие в рассмотренные координаты в виде:

x₁=x⁰₁+∆x₁, x₂=x⁰₂+∆x₂, f=f⁰+∆f, x₂=∆x₂. (4)

В системе (4) ∆x₁, ∆x₂, ∆f, ∆x₂ - отклонение соответствующих координат от их значений, принятых за исходные при линеаризации.

Соотношение (4) позволяет вместо полных значений координат x₁, x₂, f, x₂, оперировать их отклонениями (превращениями) ∆x₁, ∆x₂, ∆f, ∆x₂.

2 Левую часть уравнения (2) разлагают в ряд Тейлора относительно точки с координатами ( 0,x⁰₂,x⁰₁,f ) в соответствующей исходному режиму. В результате (2) переписывается в виде :

F(0, x⁰₂, x⁰₁, f⁰)+ +Q(∆x₂, ∆x_2, ∆x₁,∆f)=0

Здесь ⁰ - частные производные от функции F(x₂,x₂,x₁,f) по

соответствующей переменной, в которой после определения подставлены значения x₁=x⁰; x₂=x₂⁰; f=f⁰; x₂=0.

В итоге получаются некоторые числа. Символом Q - обозначим остаточный член разложения содержащий вторую или более высокие степени разложения (∆x₁, ∆x₂, ∆x₂, ∆f ) их произведение умноженное на соответствующие производные.m

3 Отклонением ∆x₂,∆x₂, ∆x₁, ∆f считают малыми и на этом основании пренебрегают остаточным членом Q (∆x₂, ∆x₂, ∆x₁, ∆f)≈0. Учитывая F (0, x₂⁰, x₁⁰, f⁰ )=0 в уравнение (5) можно получить выражение:

=0

Это уравнение есть линейное - дифференциальное уравнение с постоянными коэффициентами, оно представляет собой результат линеаризации нелинейного уравнения (2) относительно исходного режима ( x₁=x₁⁰; x₂=x₂⁰; f=f⁰;x₂=0 ). В основе этого подхода лежит допущение о малости отклонения всех коэффициентов от исходных в этом случае допустимо разложение функции F в ряд Тейлора в окрестностях точки (0; x₂⁰; x₁⁰; f⁰).

Если такое разложение не возможно, например F недеференцируема по координате, то рассматриваемый метод линеаризации неприменим, звено является существенно нелинейным. Запись линейного дифференциального уравнения в виде (6), является довольно громоздкой. В автоматике обычно опускается символ приращения «». Кроме того, принято выходную величину x₂ и ее производные записывать в левой части, а все остальные члены переносить вправо. В результате выражение (6) можно представить так:

С целью сокращения выкладок при записи дифференциальных уравнений, используется условное обозначение производных и интегралов:

-символ дифференцирования

С использованием этого символа дифференциальное уравнение первого порядка имеет вид или , в общем случае для дифференциального уравнения произвольного порядка можно записать:

(7)

В частности для уравнения второго порядка полиномы c(p), b(p) и r(p) будут иметь следующий вид:

, , , где

,для уравнения произвольного порядка символически полиномы будут иметь следующий вид:

,

,

,

В ТАУ оказывается удобным разделить все числа дифференциального уравнения на коэффициент при . В случае его отсутствия на ненулевой коэффициент при самой младшей производной от . Так для системы первого порядка поделив на получим : (*)

Т – называется постоянной времени звена и имеет размерность «секунда». Величина и , это коэффициенты передачи звена по входной величине и по возмущению соответственно.

Уравнение (*) называется линейным дифференциальным уравнением первого порядка (ЛДУ-1), в стандартной форме записи. Аналогичным образом к стандартной форме записи приводятся и уравнения более высших порядков. Например для дифференциального уравнения второго порядка (ЛДУ-2) стандартная форма записи имеет следующий вид:

,

- постоянные времени звена,

- коэффициенты передачи звена.

Передаточные функции линейных звеньев.

Уравнение (7) исчерпывающе характеризует динамические свойства звена, т.к. позволяет найти реакцию звена на любые входные сигналы и возмущения . Однако существуют более удобные и наглядные способы описания динамических свойств линейных объектов, среди них можно отличить: передаточные функции, временные и частотные характеристики.

Передаточной функцией звена по какому либо воздействию называется отношение преобразования Лапласа входной величины звена, к преобразованию Лапласа рассматриваемого воздействия.

При этом все другие воздействия полагаются равными нулю, принимаются нулевыми также начальные условия.

Для звена вида

можно ввести передаточную функцию по входной величине (1)

и передаточную функцию по возмущению (2). Здесь - комплексная переменная, это преобразования Лапласа (изображения) соответствующих функций, определяющихся следующим образом:

Использование формул (1) и (2) для вычисления передаточных функций не целесообразно. Они могут быть легко вычислены, если известно дифференциальное уравнение звена вида (7).

Преобразуем это уравнение по Лапласу, т.е. перейдем к изображению.

Согласно теоремы о линейности уравнение (7) в развернутом виде может быть записано в следующем виде:

По теории об изображении производных: , имеем

или (3), где . Решив уравнение (3) относительно получим . Положив найдем передаточную функцию звена по входной величине (4) . При получим передаточную функцию по возмущающему воздействию : (5).

Исходя из вышеперечисленного правило для определения передаточной функции звена можно записать следующим образом:

1. составить дифференциальное уравнение в символической форме

2. разделить формально символический многочлен, стоящий в правой части перед интересующим нас воздействием на символический многочлен в левой части

3. в полученном результате символ дифференцирования заменить на комплексную переменную

Пример:

Для звена первого порядка, описанного символическим уравнением , передаточная функция звена по входной величине . Сопоставив уравнения (4) и (5) видно, что передаточные функции какого-либо конкретного звена имеет один и тот же знаменатель.

Многочлен, стоящий в знаменателе называется характеристическим полиномом этого звена, а уравнение вида характеристическим уравнением звена. Корни многочлена стоящего в числителе передаточной функции, называются нулями этой передаточной функции.

Корни многочлена, стоящего в знаменателе передаточной функции, называются полюсами передаточной функции.

Графическое изображение звена.

Структурные схемы.

З апишем изображение выходной величины в следующем виде (). Представим в виде , , . Последние формулы удобно изображать графически следующим образом

Здесь выходная величина представляет собой произведение входной величины на передаточную функцию, изображенную в прямоугольнике.

Условимся результат суммирования изображать в виде перечеркнутого круга , тогда можно записать

Э тот же символ используется для обозначения разности. В этом случае сектор, соответствующий вычитаемому зачеркивается

После введенных выше графических обозначений уравнение () можно представить в виде:

Этот рисунок представляет собой структурную схему динамического звена.

Структурной схемой элемента автоматики или всей САУ называется схема, показывающая, из каких звеньев состоит объект и как эти звенья соединены между собой. Часто на структурных схемах записываются не изображения функции, а сами функции ( ). Это допустимо, но не следует забывать что, соотношения, лежащие в основе построения структурных схем, справедливы только для изображений(т.е. для функций от ).

На основании выше сказанного обобщенная структурная схема САУ может быть представлена следующим образом:

- передаточная функция датчика

- передаточная функция регулятора

- передаточная функция исполнительного устройства

- передаточная функция объекта регулирования

- передаточная функция объекта регулирования по возмущению

Передаточная функция основных соединений линейных звеньев.

САУ – представляет собой свойство звеньев по разному соединенных между собой. Существуют три типа соединений:

• последовательное

• параллельное

• соединения с обратной связью ( встречно-параллельное)

последовательным называется такое соединение двух или более звеньев, при котором выходная величина предыдущего звена является входной величиной последующего .

графически можно представить следующим образом:

Д ля такого соединения можно записать:

общая передаточная функция соединения будет равна:

; (1)

И з формулы (1) следует что последнее соединение звеньев можно заменить эквивалентной структурной схемой следующего вида:

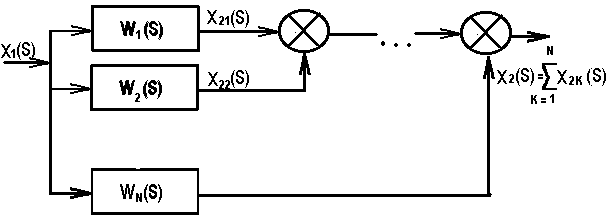
Параллельное соединение называатся такое соединение 2 или более звеньев, при котором входная величина звеньев одна и тоже, а выходные величины складываются графически:

Для каждого из звеньев можно записать:

; (2)

Э квивалентная структурная схема параллельного соединения следующая:

Соединение с обратной связью – называется соединение двух звеньев, при котором выходная величина одного звена подается обратно на вход этого звена через другое.

Г рафически изображается в виде:

Звено стоящее в прямой цепи называется звеном обхватываемым обратной связью. Звено, стоящее в цепи обратной связи (c ), называется звеном обратной связи

. Может складываться с входной величиной . В этом случае имеет место положительная обратная связь

вычитается, то отрицательная обратная связь.

Найдем изображение связывающее изображение выходной величины с изображением входной величины . ;

после подставления получим:

решим последнее уравнение относительно в результате получим:

; (3)

для соединения с отрицательной связью имеем окончательный результат:

эквивалентная структурная сема соединения с обратной связью имеет вид: (ри

В ажным случаем является единичная обратная связь

Д ля такого соединения передаточная функция следующая:

Временные характеристики линейных звеньев

Временные характеристики звена называется закон изменения выходной величины , при изменении входного по определенному закону при условии , что до приложения воздействия звено находилось в покое.

Чаще всего при получении временных характеристик, что входное воздействие изменяется по закону единичной ступенчатой функции.

либо по закону ∆-функции.

для дельта функции характерно, что площадь:

временные характеристики звена при этих законах изменений внешних воздействий получили название переходной функцией звена и функцией веса звена.

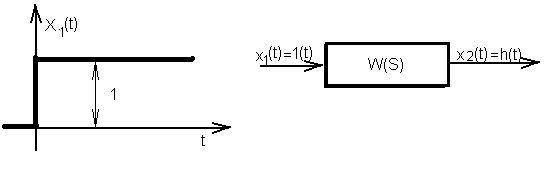
Переходной функцией звена h(t) называется реакция звена на входной сигнал X₁(t)=1(t), при условии, что до приложения входного воздействия звено находилось в покое.

Переходная функция может быть определена экспериментально или вычислено теоретически. Если работа звена описывается дифференциальным уравнением следующего вида:

то для теоретического определения h(t) необходимо найти решение уравнения в виде: при условии, что :f(t)=0; h(0)=h”(0)=…=0

Воспользовавшись преобразованием Лапласа получим изображение переходной функции т.к. изображение .

Из последней формулы следует, что переходная функция будет обратным преобразованием Лапласа от изображения

Таким образом функция представляет собой обратное преобразование Лапласа от передаточной функции деленной на S.

В общем случае передаточная функция определяется формулой

изображение переходной функции будет

результаты вычисления передаточной функции обычно представляется в виде графика в координатах t, h(t). Начальное при и конечное при значения переходной функции можно оценить, не вычисляя саму функцию h(t), по теореме о начальном значении оригинала , подставляя последнее выражение, в выражение получим

по теореме о конечном значении оригинала имеем следующее

тогда имеем

Функцией веса или импульсной переходной функцией звена называется его реакция на входной сигнал при условии, что до приложения входного воздействия звено находилось в покое.

Функция так же может быть вычислена экспериментально или теоретически. Для экспериментального определения функции веса снимаю процесс изменения выходной величины звена при входном воздействии в виде реального импульса произвольной формы с единичной площадью. Для теоретического определения функции веса необходимо решить дифференциальное уравнение следующего вида:

при нулевых начальных условиях: , преобразовав последнее уравнение по Лапласу, получим: ; .

Отсюда функция веса

Таким образом, функция веса представляет собой обратное преобразование Лапласа от передаточной функции звена. Начальное и конечное значения так же можно определить, не зная вида самой функции по соответствующим функциям: ; .

Функция веса так же строится обычно в координатах t, (t).

Найдем связь между переходной функцией и функцией веса. По теореме об изображении производной можно записать

Переход к оригиналам дает следующий результат: ; .

Функция веса является производной от переходной функции. В виду наличия однозначной связи между и , в расчетах обычно используется одна из этих характеристик. Чаще всего переходная функция, так как экспериментально определить ее проще. Рассмотренные выше характеристики полностью определяют динамические свойства звена, так же как дифференциальные уравнения и передаточные функции. В частности с помощью них можно найти реакцию звена на входное воздействие произвольной формы.

- интеграл Дюамеля.

Преимущества временных характеристик:

• наглядность и возможность экспериментального определения.

Недостатки:

• трудоемкость вычисления характеристик для дифференциальных уравнений высокого порядка.

Частотные характеристики линейных звеньев.

В реальных системах часто входной сигнал изменяется по гармоническому закону, с заданной частотой и амплитудой. При этом ставится задача нахождения параметров колебаний на выходе при известных на входе. Решение этой задачи с помощью временных характеристик представляет определенные трудности. Частотный же метод позволяет значительно проще получить реакцию звена или системы на любой периодический сигнал. Допустим, что возмущающее воздействие отсутствует ( ), а на вход звена с передаточной функцией поступает сигнал, изменяющийся по гармоническому закону: , где - круговая частота.

На выходе линейного звена после окончания переходного процесса так же будет периодический сигнал той же частоты, но с другой амплитудой и фазой: ; (1); (2).

Формулы (1) и (2) показывают, что для определения реакции звена на гармоническое воздействие достаточно знать комплексную функцию . Она получается заменой в передаточной функции комплексной переменной на , причем .

Функция называется частотной передаточной функцией и в общем виде может быть представлена так: (3)

Формула (3) может быть представлена в нескольких видах:

1) , где и

2) , где и

Функция называется амплитудно-частотной характеристикой (АЧХ) системы (звена). Функция называется фазо-частотной характеристикой (ФЧХ). Функции и называются вещественной (действительной) и мнимой частотной характеристикой системы (звена).

В координатах строится амплитудно-фазовая характеристика (АФК). Для этого, для каждой фиксированной частоты , на оси абсцисс откладываем , а по оси ординат . Точки соединяют плавной линией. Полученная кривая называется годографом.

Для вычисления значений представим (3) в виде:

,

где - действительные части числителя и знаменателя, - соответственно мнимые части.

Тогда модуль будет определяться:

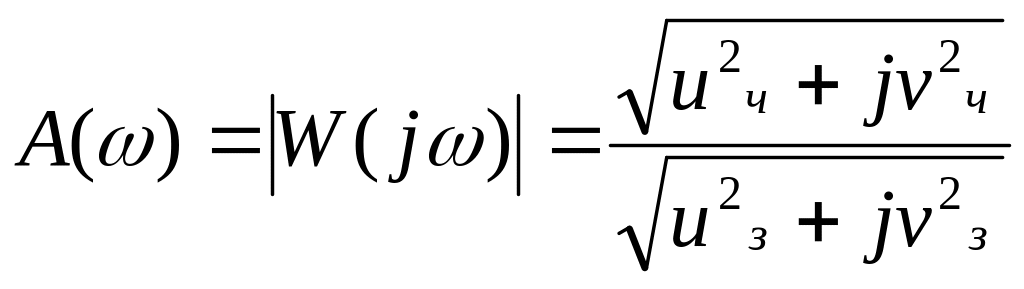
, а аргумент:

Для определения U(w) и V(w) умножим передаточную функцию на комплексно сопряженное знаменателю число.

; ; ;

.

При практических расчетах предпочтительнее пользоваться выражениями для A(w) и (w),т.к. они проще и могут быть получены экспериментально.

(w)получается как разность фаз между выходным и входным сигналами.