Гармоническое воздействие.

(1)

Такое воздействие широко применяется при оценке динамической точки САУ.

Изображение ошибки от задающего воздействия: (2)

Очевидно, что в установившемся режиме ошибка также будет меняться по гармоническому закону с частотой , амплитуда ошибки может быть определена из формулы (2) с использованием подстановки:

(3) тогда: (4)

в большинстве автоматических систем по этому выражение в знамнателе на много больше единицы.

(5)

Тогда

(6)

– значение АЧХ разомкнутой системы на частоте из уравнения (6) легко вытекает требование к АЧХ разомкнутой системы, при котором обеспечивается нужная точность управления.

Требование для АЧХ: (7)

Требование для ЛАХ: (8)

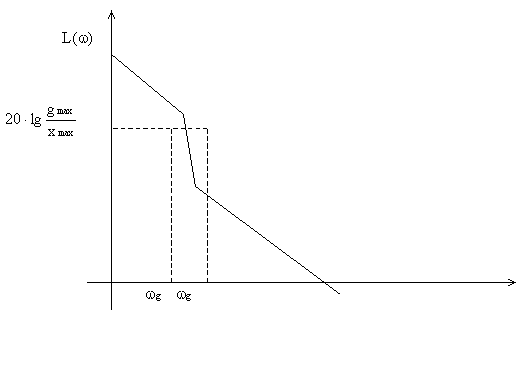Выражение (8) ограничивает местоположение ЛАХ разомкнутой системы требованиями по точности, как это показано на рисунке:

Медленно меняющееся воздействие произвольной формы

Если внешнее воздействие f(t) или g(t) имеют доступно плавную форму, то существенные значения имеет лишь конечное m число производных

; (9)

Соответствующие составляющие установившихся ошибок могут быть определены из передаточных функций замкнутой системы по ошибкам.

Разложим эти передаточные функции в ряд по возрастающим степеням S:

(10)

Эти ряды, сходящиеся при малых значениях S, то есть при достаточно больших величинах времени t, что соответствует установившемуся режиму.

Учитывая предположение об ограниченном количестве производных из формулы №9, можно получить значение установившихся ошибок от задающего воздействия g(t) и возмущения f(t)

; (11) Где – коэффициент ошибок

; ;…; (12)

Ошибка от возмущения будет:

; ;…; (13)

Коэффициент отличен от нуля только в статических системах: (14)

Для статических систем =0.

В статических системах первого порядка:

В астатических системах второго порядка: .

Коэффициенты и можно получить не по выше приведенным формулам, а путём деления многочлена на многочлен.

Для получения – .

Для получения – .

Оценка запаса устойчивости и быстродействия по частотным показателям качества.

Здесь оценка производится по частотным характеристикам замкнутой или разомкнутой систем. Достоинством этих методов является возможность использования экспериментально снятых частотных характеристик отдельных звеньев САУ.

Рассмотрим метод оценки по АЧХ замкнутой системы, её можно получить из передаточной функции замкнутой системы путём перехода (подстановки)

, тогда получим - АЧХ; - ФЧХ

Возможные очертания АЧХ замкнутой системы имеют следующий вид:

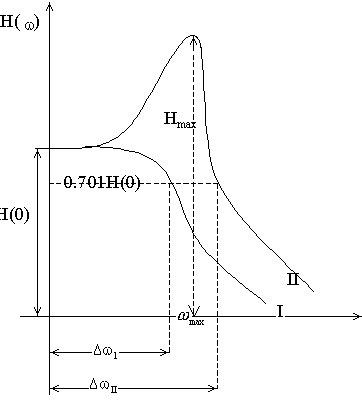
Для большинства систем управляющая характеристика H(w) имеет резонансный пик H_max.

Для систем, находящихся на колебательной границе устойчивости характеристика на частоте имеет разрыв.

Таким образом, чтобы система была достаточно удалена от границы устойчивости величина типа АЧХ H_max должна быть ограничена. Чем больше H_max, тем меньше запас устойчивости.

При исследовании САУ запас устойчивости принято оценивать по показателю колебательности М.

Под показателем М понимаем следующее значение: М

Обычно считается достаточным запас устойчивости, если показатель колебательности лежит в пределах: 1,1<= М <=1,5

Мерой быстродействия САУ может служить полоса пропускания определяются по виду АЧХ замкнутой системы. Чем шире полоса пропускания, тем выше быстродействие системы.

Показателю колебательности М >1 соответствует резонансная частота , которая приблизительно равна частоте колебания замкнутой системы в переходном процессе. При этом время достижения I перерегулирования будет примерно равно:

При условии, что переходный процесс заканчивается за одно, два колебания:

О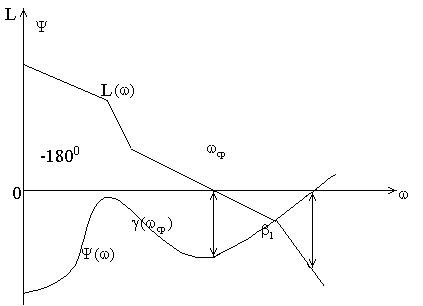 запасе устойчивости также можно судить по логарифмическим частотным характеристикам (ЛЧХ) разомкнутой системы, то есть по ЛАХ и ЛФХ. По ним определяется запас устойчивости по фазе и запас устойчивости по амплитуде.

Запас устойчивости по амплитуде определяется на частоте

Такой запас устойчивости считается достаточным, если

(14)

запас устойчивости по амплитуде определяется по ЛАХ при частоте, на которой равняется 180градусов.

запас устойчивости по амплитуде равняется: (15)

Запас по амплитуде считается достаточным, если он больше .

По логарифмическим характеристикам также можно оценить быстродействие системы

По виду переходных функций также можно оценить запас устойчивости и быстродействия.

Запас устойчивости определяется перерегулированием: (16) где

Переходный процесс считается закончившимся, если:

(17)