Содержание отчета
Наименование работы.
Цель работы.
Оборудование, приборы, инструменты.
Схема и описание принципа работы прибора ЭХО-1.
Результаты измерений диаметров отпечатков для различных материалов и условий испытаний.
Результаты расчета средних значений и коэффициентов вариации диаметров отпечатков для различных материалов и условий испытаний.
Графики зависимостей средних диаметров отпечатков от времени приложения нагрузки и величины прикладываемой нагрузки.
Выводы.
Контрольные вопросы
Назовите преимущества моделирования процесса износа перед его оценкой в процессе резания.
Назовите назначение и принцип работы прибора ЭХО – 1.
Как осуществляют измерение диаметров отпечатков.
Почему при оценке значений диаметров выполняют повторные опыты?
Позволяет ли метод моделирования процесса износа оценить износостойкость инструментов или других объектов?
Назовите недостатки моделирования процесса износа перед оценкой износа в процессе резания.
1.2.3 Лабораторная работа №3
Получение математических моделей зависимости износа образцов от величины и времени приложения нагрузки
Цель работы – получить математические модели зависимости износа образцов из стали Р6М5 и образцов из стали Р6М5 упрочненных импульсным магнитным полем (Р6М5+ОИМП) от величины и времени приложения нагрузки с использованием полного факторного эксперимента типа 22.
Оборудование, приборы, инструменты, заготовки
Прибор ЭХО-1.
Образцы из стали Р6М5 и Р6М5, упрочненных импульсным магнитным полем (Р6М5+ОИМП).
Набор грузов.
Инструментальный микроскоп.
Содержание и порядок выполнения работы
В лабораторных условиях при моделировании износа на приборе ЭХО-1проводят ПФЭ типа 22 с целью получения математической модели зависимости износа (диаметра отпечатка d) от времени приложения (τ) и величины нагрузки (p).
Для каждой переменной (фактора) выбирают два уровня ее измерения: верхний (+1) и нижний (-1). Каждому фактору присваивают соответствующее кодовое значение: τ=х1, Р=х2, d=x2, d=y. Значения факторов приведены в таблице 1.10.
Таблица 1.10 – Уровни независимых факторов
-
Уровень
Значение факторов
τ (х1), с
Р(х2), кг
Нижний (-1)
60
0,155
Нулевой (0)
75
0,203
Верхний (+1)
90
0,250
Строят матрицы ПФЭ для образцов из стали Р6М5 и (Р6М5+ОИМП) (таблица 1.11, 1.12). Минимальное количество опытов N=22=4. Для исключения влияния различных случайных факторов проводят рандомизацию опытов (при их трехкратном повторении). Методика получения диаметров отпечатков приведена в п. 1.2.1. Результаты опытов заносят в таблицу 1.11 и 1.12.
Математическая модель износа образцов от величины и времени приложения нагрузки должна быть получена в виде
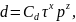(1.23)
где
– постоянный коэффициент, учитывающий
свойства образцов и условий испытаний;
x, z – показатели степеней.
Для получения степенных зависимостей используют логарифмические масштабы. После логарифмирования обеих частей формулы (1.23) и ведения членов, учитывающих взаимодействие факторов, уравнение регрессии будет иметь вид
,
(1.24)
где
– логарифм диаметра отпечатка;
– коэффициент
регрессии;
– логарифмы
времени и величины нагрузки.
Для расчета коэффициентов регрессии используют столбцы матрицы ПФЭ и логарифмы средних значений диаметров отпечатков (
).
В качестве примера можно использовать
расчеты по формуле (1.17).Дисперсию, характеризующую ошибку опыта, рассчитывают по формуле (1.7).
Дисперсию параметра оптимизации у рассчитывают по формуле (1.8).
Проводят оценку однородности дисперсий по Gкр. Кохрена по формуле (1.9). Если дисперсии не однородны, то в точке плана с максимальной дисперсией выполняют повторные опыты. Расчеты повторяют с использованием вновь полученных значений
.Рассчитывают дисперсию коэффициента регрессии по формуле (1.10).
Выполняют проверку значимости коэффициентов регрессии по tкр. Стьюдента (формула 1.11).
С учетом значимых коэффициентов bi записывают полученное уравнение регрессии и используют его для расчета
(значений
по модели). Результаты расчетов записывают
в таблицы 1.11, 1.12.Рассчитывают дисперсию адекватности (формула 1.12).
Производят проверку адекватности полученной модели по критерию Фишера (формула 1.14).
Таблица 1.11 – Матрица ПФЭ типа 22 и результаты измерений диаметров отпечатков (образцы из стали Р6М5)
-
№ опыта
,
с
,
кГx0
x1
x2
x1x2
Текущие значения у
Средние у
Дисперсия опыта
Значение по нормали
у1
ln у1
у2
lnу2
у3
lnу3
1,5,9
60
0,155
+
-
-
+
57,5
60,0
62,5
2,6,10
90
0,155
+
+
-
-
70,7
72,5
75,0
3,7,11
60
0,250
+
-
+
-
80,8
83,0
85,0
4,8,12
90
0,250
+
+
+
+
95,0
100,0
98,0
Таблица 1.12 – Матрица ПФЭ типа 22 и результаты измерений диаметров отпечатков (образцы из стали Р6М5+ОИМП)
-
№ опыта
, с
, кГ
x0
x1
x2
x1x2
Текущие значения у
Средние у
Дисперсия опыта
Значение по нормали
у1
ln у1
у2
lnу2
у3
lnу3
1,5,9
60
0,155
+
-
-
+
42,5
40,0
40,0
2,6,10
90
0,155
+
+
-
-
52,5
50,0
55,0
3,7,11
60
0,250
+
-
+
-
65,0
60,0
65,0
4,8,12
90
0,250
+
+
+
+
80,0
85,0
90,0
Переход от кодированных значений х1 и х2 к натуральным переменным τ и Р осуществляют по формулам
(1.25)
Значения х1 и х2, выраженные формулами (1.25) подставляют в полученные уравнения регрессии. Для получения степенных зависимостей результаты потенцируют.