
- •Содержание
- •Введение
- •1Лабораторный практикум
- •1.1Получение математических моделей процессов резания методом полного факторного эксперимента
- •Статистическое планирование эксперимента. Выбор параметра оптимизации и независимых факторов. Построение матриц полного факторного эксперимента.
- •1.1.2 Получение математической модели
- •1.1.3 Проверка адекватности модели
- •1.1.4 Лабораторная работа №1
- •Содержание отчета
- •Контрольные вопросы
- •1.2 Получение математических зависимостей моделированием процессов износа изделий и материалов
- •1.2.1 Особенности моделирования процесса износа
- •1.2.2 Лабораторная работа №2 Исследование износостойкости различных материалов моделированием процесса износа
- •Содержание и порядок выполнения работы
- •Содержание отчета
- •Контрольные вопросы
- •1.2.3 Лабораторная работа №3
- •Оборудование, приборы, инструменты, заготовки
- •Содержание и порядок выполнения работы
- •Содержание отчета
- •Контрольные вопросы
- •1.3 Построение моделей в среде Excel for Windows
- •1.3.1 Построение линейной модели в Excel (пример)
- •1 Настройка пакета анализа
- •2 Ввод данных
- •3 Нахождение основных числовых характеристик
- •4 Нахождение коэффициента корреляции
- •5 Нахождение параметров линейной регрессии
- •6 Расчет доверительного интервала для прогноза
- •7 Построение доверительной области для прогноза
- •8 Расчет максимального % ошибки прогнозирования
- •9 Выводы по работе
- •1.3.2 Построение степенной модели в Excel (пример)
- •1 Настройка пакета анализа
- •2 Ввод данных
- •3 Нахождение основных числовых характеристик
- •4 Нахождение коэффициента корреляции
- •5 Нахождение параметров линейной регрессии
- •1.3.3. Пример построения многофакторной линейной модели в Excel
- •1 Настройка пакета анализа
- •2 Ввод данных
- •3 Нахождение основных числовых характеристик
- •4 Нахождение параметров линейной регрессии
- •5 Выводы по работе
- •1.3.4 Лабораторная работа № 4 Построение однофакторных регрессионных моделей в приложении
- •Содержание и порядок выполнения работы
- •Содержание отчета
- •Контрольные вопросы
- •1.3.5 Лабораторная работа № 5 Построение линейной многофакторной модели в приложении
- •2 Методические указания к практическим занятиям
- •2.1 Моделирование процесса резания методом линейного программирования Практическое занятие 1
- •2.1.2 Содержание отчёта
- •2.1.3 Контрольные вопросы
- •2.2 Исследование вероятностных эксплуатационных характеристик режущих инструментов Практическое занятие 2
- •2.2.1 Содержание и порядок выполнения работы
- •2.2.2 Содержание отчета
- •2.2.3 Контрольные вопросы
- •2.3 Определение закона распределения периода стойкости инструмента при малых объемах испытаний Практическое занятие 3
- •2.3.1 Содержание и порядок выполнения работы
- •2.3.2 Содержание отчета
- •2.4 Получение математических моделей методом полного факторного эксперимента Практическое занятие 4
- •2.4.1 Содержание и порядок выполнения работы
- •2.4.2 Содержание отчёта
- •2.4.3 Контрольные вопросы
- •2.5 Получение математических моделей методами теории корреляции Практическое занятие 5
- •2.5.1 Содержание и порядок выполнения работы
- •2.5.2 Содержание отчета
- •2.5.3 Контрольные вопросы
- •3.1 Задание на расчетно-графическую работу
- •3.2 Порядок выполнения работы
- •3.3 Проверка соответствия статистического распределения теоретическому по критерию Пирсона (æ²)
- •3.4 Проверка соответствия статистического распределения теоретическому по критерию Колмогорова (n)
- •Статистическое, 2- теоретическое;
- •Список рекомендованной литературы
- •Приложение а Справочные таблицы для проверки адекватности математических моделей
- •Приложение б Пример выполнения расчетно-графической работы
- •84313, М. Краматорськ, вул. Шкадінова, 72
Приложение б Пример выполнения расчетно-графической работы
Рассмотрим расчёт вероятностных эксплуатационных характеристик режущего инструмента и проверку соответствия статистического и теоретического распределения периода стойкости по критерию Пирсона (χ 2), используя для этого значения периода стойкости токарных сборных резцов Н×В=25×25 мм, оснащённых твёрдым сплавом Т5К10.
Расчёт выполняют в следующей последовательности.
1 Располагают данные о периоде стойкости резцов в вариационный ряд (таблица Б.1).
Таблица Б.1 – Вариационный ряд периода стойкости
Номер испыта-ний i |
Период
стой-кости
|
Номер испыта-ний i |
Период стой-кости , мин |
Номер испыта-ний i |
Период стой-кости , мин |
Номер испыта-ний i |
Период стой-кости , мин |
1 |
10 |
10 |
15 |
19 |
20 |
28 |
22 |
2 |
10 |
11 |
15 |
20 |
20 |
29 |
22 |
3 |
10 |
12 |
18 |
21 |
20 |
30 |
22 |
4 |
15 |
13 |
18 |
22 |
20 |
31 |
25 |
5 |
15 |
14 |
18 |
23 |
20 |
32 |
25 |
6 |
15 |
15 |
18 |
24 |
20 |
33 |
25 |
7 |
15 |
16 |
18 |
25 |
20 |
34 |
27 |
8 |
15 |
17 |
18 |
26 |
22 |
|
|
9 |
15 |
18 |
18 |
27 |
22 |
|
|
2 Вариационный ряд разбивают на интервалы. Число интервалов рассчитывают по формуле
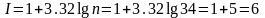 ,
(Б.1)
,
(Б.1)
где n = 34 – количество (объём) исходных данных.
3 Рассчитывают среднее значение периода стойкости
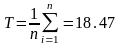 ,
мин
(Б.2)
,
мин
(Б.2)
4 Рассчитывают среднее квадратичное отклонение периода стойкости
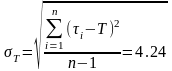 ,
мин (Б.3)
,
мин (Б.3)
5 Рассчитывают коэффициента вариации периода стойкости
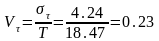 (Б.4)
(Б.4)
6
Исходя из значений коэффициента вариации,
принимаем гипотезу о нормальном законе
распределения периода стойкости (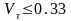 ).
).
7
Для проверки гипотезы о нормальном
законе распределения необходимо
рассчитать вероятностные эксплуатационные
характеристики (показатели надёжности)
резцов: плотность распределения
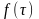 ,
интенсивность отказов
,
интенсивность отказов
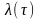 и вероятность безотказной работы
и вероятность безотказной работы
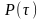 ,
которую затем используют для расчёта
критерия χ2.
Значения показателей надёжности
рассчитывают для интервалов времени
от
,
которую затем используют для расчёта
критерия χ2.
Значения показателей надёжности
рассчитывают для интервалов времени
от
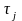 до
до
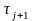 :
:
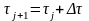 ,
(Б.5)
,
(Б.5)
где
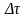 - величина интервала.
- величина интервала.
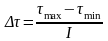 ,
(Б.6)
,
(Б.6)
где
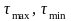 - максимальное и минимальное значение
периода стойкости из вариационного
ряда;
- максимальное и минимальное значение
периода стойкости из вариационного
ряда;
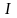 количество
интервалов.
количество
интервалов.
В нашем случае
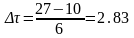 .
.
Для
удобства расчётов принимаем
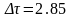 .
.
Данные расчётов удобно свести в таблицу Б.2, которая содержит все необходимые показатели для проверки по критерию χ2.
8
Рассчитывают число отказов
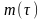 за интервал
,
используя для этого вариационный ряд.
за интервал
,
используя для этого вариационный ряд.
9
Рассчитывают статистические значения
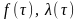 и
(формулы
для расчёта приведены в таблице .2).
и
(формулы
для расчёта приведены в таблице .2).
10 Для каждого интервала рассчитывают теоретические значения по формуле
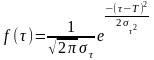 ,
(Б.7)
,
(Б.7)
где - среднее значения периода стойкости для каждого интервала.
Результаты расчётов заносят в таблицу Б.2.
11 Для каждого интервала рассчитывают теоретическое значение по формуле
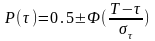 ,
(Б.8)
,
(Б.8)
где
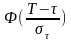 - функция Лапласа. Значения функции
Лапласа приведены в таблице 3.5;
- функция Лапласа. Значения функции
Лапласа приведены в таблице 3.5;
- значение периода стойкости в начале каждого интервала.
Результаты расчётов заносят в таблицу Б.2.
12 Для каждого интервала рассчитывают теоретическое значение по формуле
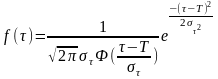 или
или
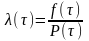 (Б.9)
(Б.9)
Результаты расчётов заносят в таблицу Б.2.
13 Расчёт χ2 выполняют по формулам, приведенным в столбцах 13…17 таблицы Б.2. Сумма значений строк столбца 17 представляет собой значение χ2.
14
Расчётное значение χ2
сравнивают
с табличным χ2табл.
Расчётное значение χ2
не
должно быть больше табличного (χ2≤
χ2табл).
Табличные значения χ2
выбирают из таблицы 3.7 при числе степеней
свободы
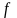 ,
которое рассчитывают по формуле
,
которое рассчитывают по формуле
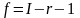 ,
(Б.10)
,
(Б.10)
где - число интервалов;
- число параметров закона распределения.
В нашем случае
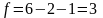
Табличное
значение χ2табл
=
7,81 при уровне значимости
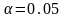 .
.
Таким образом, гипотеза о соответствии статистического и теоретического распределения нормальному закону выбрана правильно (1,94<7,81).
15 По результатам расчётов строят графики и для статистического и теоретического распределений (рис. Б.1…Б.3).
16
При проверке соответствия статистического
и теоретического распределения по
критерию Колмогорова
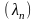 находят максимальное отклонение
вероятности безотказной работы для
статистического и теоретического
распределения
находят максимальное отклонение
вероятности безотказной работы для
статистического и теоретического
распределения
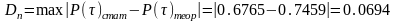 .
(Б.11)
.
(Б.11)
17 Рассчитывают значение критерия Колмогорова
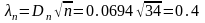 (Б.12)
(Б.12)
По
таблице 3.8 для каждого полученного
значения
находим
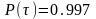 .
Это значит, что статистическое и
теоретическое распределение согласуются
с вероятностью
.
Это значит, что статистическое и
теоретическое распределение согласуются
с вероятностью
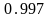 .
.
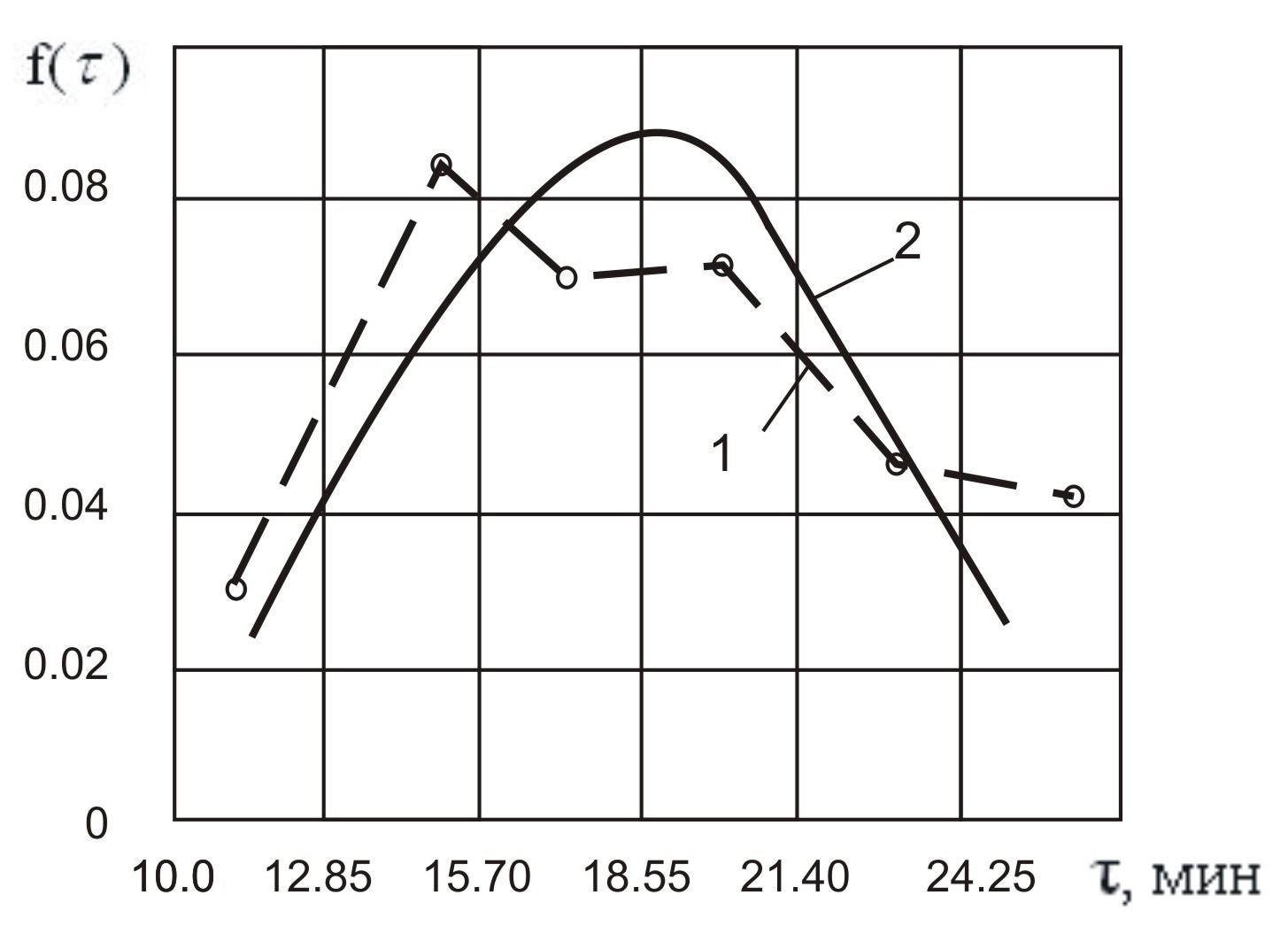
1 – статистическое распределение; 2 – теоретическое распределение
Рисунок Б.1 – Плотность распределения периода стойкости
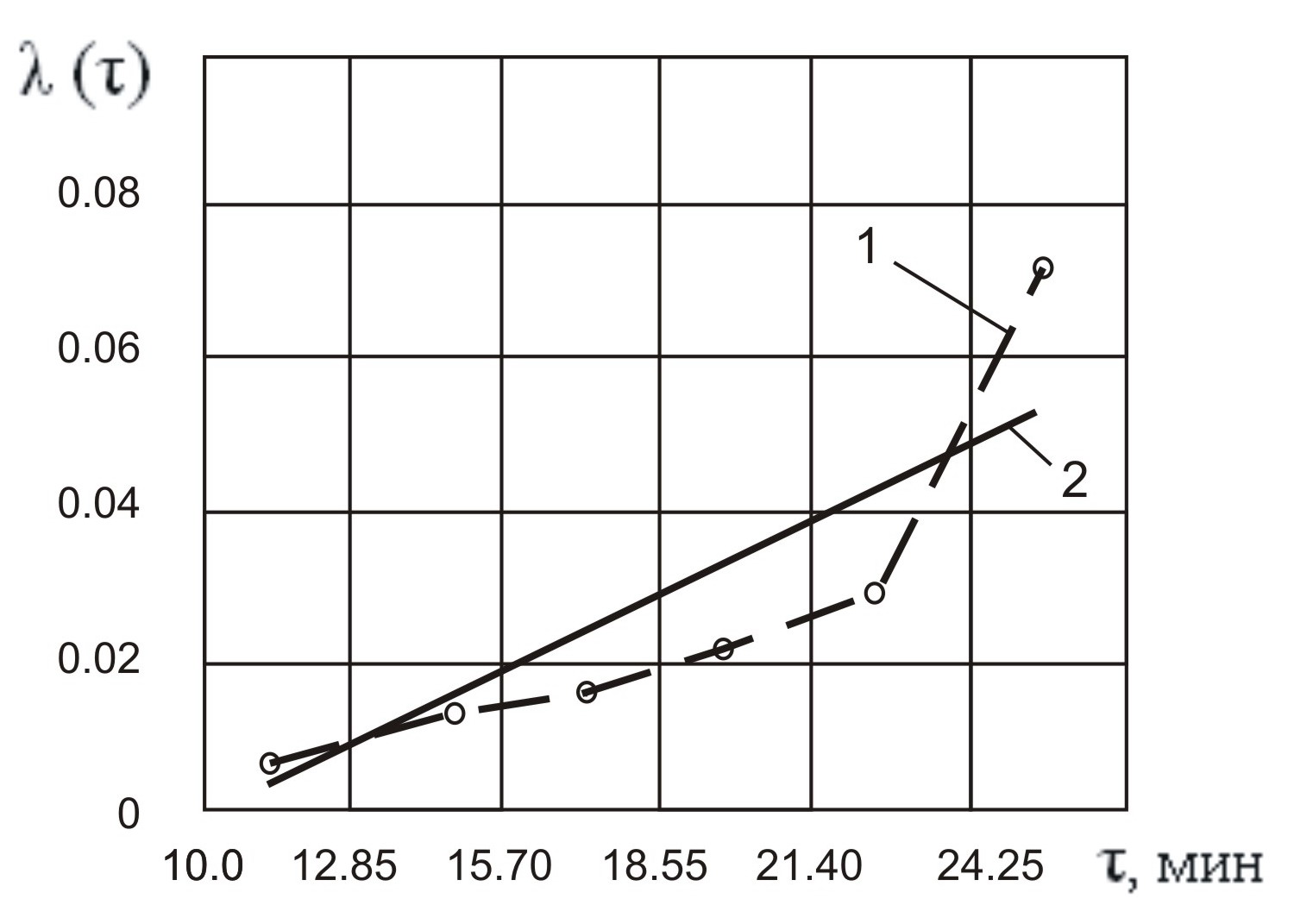
1 – статическое распределение; 2 – теоретическое распределение
Рисунок Б.2 – Интенсивность отказов
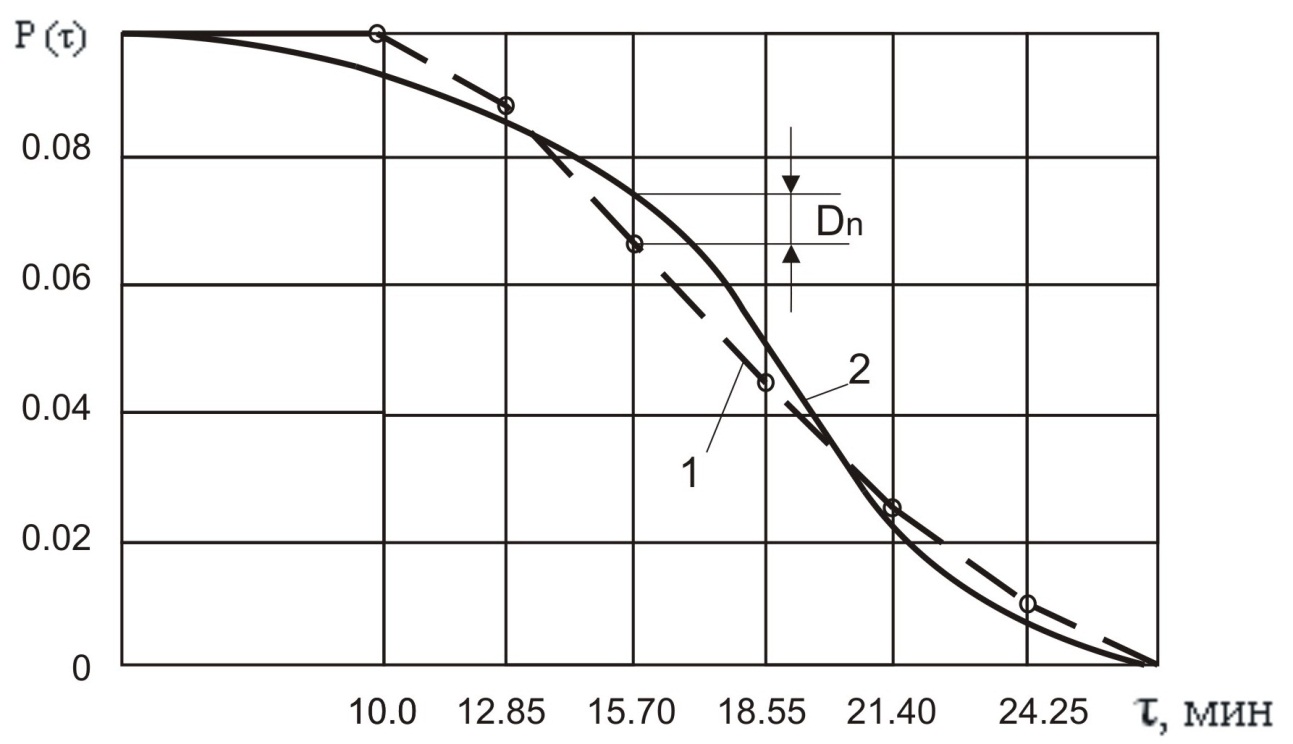
1 – статическое распределение; 2 – теоретическое распределение
Рисунок Б.3 – Вероятность безотказной работы
Таблица Б.2 – Вероятностные эксплуатационные характеристики режущего инструмента.
Проверка статистического и теоретического распределения по критерию Пирсона (χ2)
Номер интервала j |
Граница интервала Δτ =τj+1-τj |
Число отказов за интервал Δτ |
Число работоспособных инструментов в момент времени τj |
Среднее число работоспособных инструментов |
Плотность распределения f(τ) |
Интенсивность отказов λ(τ) |
Вероятность безотказной работы Р(τ) |
К проверке соответствия статистического и теоретического распределения по критерию Пирсона |
|||||||||||
τj |
τj+1 |
m(τ) |
n(τ) |
(nj+nj+1)/2 |
Статическая m(τ)/nΔτ |
Теоретическая |
2 m(τ)/ (nj+nj+1)Δτ |
Теоретическая |
n(τ)/n |
Теоретическая |
ΔP(τ)=P(τj)-P(τj+1) |
nΔP(τ) |
m(τ)- nΔP(τ) |
[m(τ)- nΔP(τ)]2 |
[m(τ)- nΔP(τ)]2/ [nΔP(τ)] |
||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|||
1 |
10,00 |
12,85 |
3 |
34 |
32,5 |
0,0311 |
0,0236 |
0,0326 |
0,0247 |
1,0000 |
1,0000 |
0,0917 |
-3,1178 |
-0,1178 |
0,0139 |
0,0044 |
|||
2 |
12,85 |
15,70 |
8 |
31 |
27,0 |
0,0830 |
0,0573 |
0,1040 |
0,0682 |
0,9118 |
0,9083 |
0,1624 |
5,5216 |
2,4784 |
6,1425 |
1,1124 |
|||
3 |
15,70 |
18,55 |
7 |
23 |
19,5 |
0,0727 |
0,0892 |
0,1267 |
0,1420 |
0,6765 |
0,7459 |
0,2487 |
8,4558 |
-1,4558 |
2,1194 |
0,2506 |
|||
4 |
18,55 |
21,40 |
7 |
16 |
12,5 |
0,0727 |
0,0788 |
0,1967 |
0,2424 |
0,4706 |
0,4972 |
0,2476 |
8,4184 |
-1,4181 |
2,0118 |
0,2390 |
|||
5 |
21,40 |
24,25 |
5 |
9 |
6,5 |
0,0519 |
0,0565 |
0,2715 |
0,3618 |
0,2647 |
0,2496 |
0,1602 |
5,4468 |
-0,4468 |
0,1996 |
0,0366 |
|||
6 |
24,25 |
27,10 |
4 |
4 |
2,0 |
0,0415 |
0,0230 |
0,7059 |
0,4937 |
0,1176 |
0,0894 |
0,0894 |
3,0396 |
0,9604 |
0,9224 |
0,3034 |
|||
Объём данных n=34 |
Коэффициент вариации Vτ=0,23 |
Число параметров закона распределения r=2 |
Критерий χ2= |
Σ= 1.9434 |
|||||||||||||||
Среднее значение Т=18,47 |
Среднее квадратичное отклонение στ=4,24 |
Параметры закона: Т=18,47; στ=4,24 |
f=j-r-1=3 |
||||||||||||||||
Теоретическое распределение - нормальное |
|||||||||||||||||||
Навчальне посібник
Казакова Тетяна Валентинівна, доц.
Васильева Людмила Володимирівна, доц.
Ковальов Денис Геннадійович, ас.
Математичне моделювання
процесів різання та різальних інструментів
Навчальний посібник
Редактор
Комп’ютерна верстка О.П. Одріна
/2011. Підп. до друку. Формат 60х84/16
Папір офсетний. Ум. друк. арк. Обл. – вид. арк..
Тираж прим. Зам. №
Донбаська державна машинобудівна академія

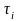 ,
мин
,
мин