2.4.2 Содержание отчёта
1 Название и цель работы.
2 Исходные данные для получения математической модели.
3 Матрица планирования эксперимента.
4 Результаты расчёта коэффициентов регрессии .
5 Результаты расчёта дисперсии опыта, дисперсии адекватности и дисперсии коэффициента регрессии с проверкой по критерию Кохрена, (таблица 2.11).
6 Проверка значимости коэффициентов регрессии по критерию Стьюдента.
7
Результаты расчёта дисперсии адекватности
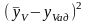(таблица 2.11).
8 Проверка адекватности математической модели по критерию Фишера.
9 Выводы.
2.4.3 Контрольные вопросы
1 Что называют параметром оптимизации при полном факторном эксперименте (ПФЭ)?
2 Что называют факторами при ПФЭ? Как выбирают интервалы измерения факторов?
3 Что называют полным факторным экспериментом?
4 Как определяют минимальное количество опытов при ПФЭ?
5 Назовите основные принципы построения матриц ПФЭ.
6 Какие свойства имеет матрица ПФЭ?
7 Как рассчитывают коэффициенты регрессии?
8 Как определяют дисперсию, характеризующую ошибку опыта?
9 Как проверяют однородность дисперсии?
10 Как проверяют значимость коэффициентов регрессии?
11 Как проверяют адекватность модели?
2.5 Получение математических моделей методами теории корреляции Практическое занятие 5
Цель работы: для заданных значений х и у получить зависимость у=f(x) методом корреляционного анализа. Рассчитать коэффициент парной корреляции и коэффициенты корреляционного уравнения. Записать корреляционное уравнение, определить точность прогнозирования у по полученному уравнению. Исходные данные взять из таблицы 2.12.
Таблица 2.12 – Исходные данные для получения корреляционной зависимости
№ варианта |
Условия задачи |
||||||||||||||
1 |
2 |
||||||||||||||
1 |
Определить коэффициенты корреляционного уравнения зависимости периода стойкости резцов (Т, мин) от скорости резания (V, м/мин). Материал режущей части резца Т5К10, S=0,6 мм/об. Записать корреляционное уравнение. Определить точность прогнозирования периода стойкости по полученному уравнению
|
||||||||||||||
2 |
Определить коэффициенты корреляционного уравнения зависимости периода стойкости резцов (Т, мин) от толщины пластины (h, мм). Материал резцов Т5К10, режимы резания: V=80 м/мин, t=5,0 мм, S=0,8 мм/об. Определить точность прогнозирования Т(y) по полученному уравнению
|
Продолжение таблицы 2.12
1 |
2 |
||||||||||||
3 |
Построить график зависимости периода стойкости свёрл (диаметр 6,0 мм, Р6М3) от толщины сердцевины. Определить коэффициенты корреляционного уравнения зависимости периода стойкости Т(мин) от толщины сердцевины dс (мм). Записать корреляционное уравнение. Определить точность прогнозирования Т по полученному уравнению
|
||||||||||||
4 |
Получить степенную корреляционную зависимость разрушающей подачи Sр (мм/об) от толщины пластины (h, мм). Рассчитать коэффициент парной корреляции. Определить точность прогнозирования Sр по корреляционному уравнению
|
||||||||||||
5 |
Получить степенную корреляционную зависимость между разрушающей подачи SР периодом стойкости резцов в эксплуатации ТЭ (мин). Резцы: НхВ=25х25 мм; t=0,3 мм; S=0,6 мм/об; V=60 м/мин. Рассчитать коэффициент парной корреляции. Сделать вывод о наличии корреляционной зависимости
|
||||||||||||
6 |
Получить корреляционное уравнение зависимости главной составляющей силы резания Рz (Н) от глубины резания t(мм). Условия работы: резцы НхВ=25х25 мм; Т5К6; S=0,6 мм/об; V=60 м/мин. Определить точность прогнозирования Рz по полученному уравнению.
|
||||||||||||
7 |
Получить корреляционное уравнение зависимости периода стойкости свёрл Т(мин) от толщины сердцевины dс (мм). Свёрла Р6М5, диаметр 6,0 мм. Определить точность прогнозирования Т по полученному уравнению
|
Продолжение таблицы 2.12
1 |
2 |
||||||||||||||
8 |
Построить график зависимости периода стойкости резцов Тэ (мин) от прочности (Sр– разрушающая подача, мм/об). Определить коэффициент парной корреляции между Тэ и Sр. Сделать вывод о тесноте связи.
|
||||||||||||||
9 |
Построить график зависимости периода стойкости резцов Т (мин) от угла заострения режущей пластины β (град). Рассчитать коэффициент парной корреляции между Т и β. Сделать вывод о наличии корреляционной зависимости.
|
||||||||||||||
10 |
Построить график зависимости периода стойкости метчиков Т(мин) от толщины сердцевины dс (мм). Метчики: Р6М5, М6 0,75. Получить степенную корреляционную зависимость Т от dс . Рассчитать точность прогнозирования Т по корреляционному уравнению
|
||||||||||||||
11 |
Получить степенную корреляционную зависимость прочности твердосплавной пластины (величины разрушающей подачи) Sр (мм/об) и от угла заострения β (град). Рассчитать коэффициент парной корреляции и проверить его значимость. Сделать вывод о наличии корреляционной зависимости
|
||||||||||||||
12 |
Получить степенную корреляционную зависимость периода стойкости резцов Т(мин) от скорости резания V(м/мин). Рассчитать коэффициент парной корреляции и проверить его значимость. Сделать вывод о наличии корреляционной зависимости. Резцы: НхВ=20 20 мм; Т15К6; t=3,0 мм; S=0,4 мм/об
|
Продолжение таблицы 2.12
1 |
2 |
||||||||||||||
13 |
Получить корреляционное уравнение зависимости периода стойкости спиральных свёрл Т(мин) от толщины сердцевины dс (мм). Свёрла Р6М5, диаметр 5,0 мм. Построить график зависимости Т от dC. Рассчитать точность прогнозирования периода стойкости по корреляционному уравнению
|
||||||||||||||
14 |
Получить корреляционное уравнение зависимости периода стойкости резцов Т(мин) от твёрдости (НВ). Материал резцов: Т15К6; режимы резания: t=3,0 мм; S=0,4 мм/об; V=80 м/мин. Рассчитать коэффициент парной корреляции и проверить его значения. Сделать вывод о наличии корреляционной зависимости
|
||||||||||||||
15 |
Получить степенную корреляционную зависимость прочности твёрдо сплавных пластин (Sр, мм/об – разрушающая подача)от глубины резания (t, мм). Построить график зависимости SP от t. Рассчитать точность прогнозирования SP по корреляционному уравнению
|
||||||||||||||
16 |
Получить корреляционное уравнение зависимости износа по задней поверхности (hз , мм) от времени работы токарного резца (τ, мин). Рассчитать коэффициент парной корреляции и проверить его значимость. Рассчитать точность прогнозирования hз по корреляционному уравнению
|
Продолжение таблицы 2.12
1 |
2 |
||||||||||||||
17 |
Получить степенную зависимость периода стойкости концевых фрез Т(мин) от скорости фрезерования V(м/мин). Обрабатываемый материал – сталь 45. Фреза Р9К10, DФ=30 мм, ширина фрезерования В=20 мм, t=3,0 мм, подача на зуб SZ=0,03 мм/зуб. Построить график зависимости Т от V. Рассчитать точность прогнозирования периода стойкости по корреляционному уравнению
|
||||||||||||||
18 |
Получить корреляционную зависимость периода стойкости спирального сверла Т(количество просверленных отверстий до износа) от скорости резания V(м/мин). Сверло: Р9К10, диаметр 9,8 мм. Обрабатываемый материал – сталь 45, подача S=0,2 мм/об. Рассчитать коэффициент парной корреляции. Сделать вывод о наличии корреляционной зависимости
|
||||||||||||||
19 |
Получить корреляционную зависимость объёмного износа (Q, мм3) алмазного резца от времени работы (τ, мин). Резец алмазный АС-4, Н В=12 12 мм, обрабатываемый материал – алюминий. Режимы резания: t=0,2 мм, S=0,01 мм/об, V=260 м/мин. Рассчитать коэффициент парной корреляции, сделать вывод о наличии корреляционной зависимости
|
||||||||||||||
20 |
Определить коэффициенты корреляционного уравнения зависимости периода стойкости развёрток (Т, мин) от скорости резания (V, м/мин). Развёртки: Р6М5, диаметр 10 мм, обрабатываемый материал – сталь 45. Режимы резания: t=0,1 мм; S=0,24 мм/об. Записать корреляционное уравнение. Сделать вывод о наличии корреляционной зависимости.
|