- •Содержание
- •Введение
- •1Лабораторный практикум
- •1.1Получение математических моделей процессов резания методом полного факторного эксперимента
- •Статистическое планирование эксперимента. Выбор параметра оптимизации и независимых факторов. Построение матриц полного факторного эксперимента.
- •1.1.2 Получение математической модели
- •1.1.3 Проверка адекватности модели
- •1.1.4 Лабораторная работа №1
- •Содержание отчета
- •Контрольные вопросы
- •1.2 Получение математических зависимостей моделированием процессов износа изделий и материалов
- •1.2.1 Особенности моделирования процесса износа
- •1.2.2 Лабораторная работа №2 Исследование износостойкости различных материалов моделированием процесса износа
- •Содержание и порядок выполнения работы
- •Содержание отчета
- •Контрольные вопросы
- •1.2.3 Лабораторная работа №3
- •Оборудование, приборы, инструменты, заготовки
- •Содержание и порядок выполнения работы
- •Содержание отчета
- •Контрольные вопросы
- •1.3 Построение моделей в среде Excel for Windows
- •1.3.1 Построение линейной модели в Excel (пример)
- •1 Настройка пакета анализа
- •2 Ввод данных
- •3 Нахождение основных числовых характеристик
- •4 Нахождение коэффициента корреляции
- •5 Нахождение параметров линейной регрессии
- •6 Расчет доверительного интервала для прогноза
- •7 Построение доверительной области для прогноза
- •8 Расчет максимального % ошибки прогнозирования
- •9 Выводы по работе
- •1.3.2 Построение степенной модели в Excel (пример)
- •1 Настройка пакета анализа
- •2 Ввод данных
- •3 Нахождение основных числовых характеристик
- •4 Нахождение коэффициента корреляции
- •5 Нахождение параметров линейной регрессии
- •1.3.3. Пример построения многофакторной линейной модели в Excel
- •1 Настройка пакета анализа
- •2 Ввод данных
- •3 Нахождение основных числовых характеристик
- •4 Нахождение параметров линейной регрессии
- •5 Выводы по работе
- •1.3.4 Лабораторная работа № 4 Построение однофакторных регрессионных моделей в приложении
- •Содержание и порядок выполнения работы
- •Содержание отчета
- •Контрольные вопросы
- •1.3.5 Лабораторная работа № 5 Построение линейной многофакторной модели в приложении
- •2 Методические указания к практическим занятиям
- •2.1 Моделирование процесса резания методом линейного программирования Практическое занятие 1
- •2.1.2 Содержание отчёта
- •2.1.3 Контрольные вопросы
- •2.2 Исследование вероятностных эксплуатационных характеристик режущих инструментов Практическое занятие 2
- •2.2.1 Содержание и порядок выполнения работы
- •2.2.2 Содержание отчета
- •2.2.3 Контрольные вопросы
- •2.3 Определение закона распределения периода стойкости инструмента при малых объемах испытаний Практическое занятие 3
- •2.3.1 Содержание и порядок выполнения работы
- •2.3.2 Содержание отчета
- •2.4 Получение математических моделей методом полного факторного эксперимента Практическое занятие 4
- •2.4.1 Содержание и порядок выполнения работы
- •2.4.2 Содержание отчёта
- •2.4.3 Контрольные вопросы
- •2.5 Получение математических моделей методами теории корреляции Практическое занятие 5
- •2.5.1 Содержание и порядок выполнения работы
- •2.5.2 Содержание отчета
- •2.5.3 Контрольные вопросы
- •3.1 Задание на расчетно-графическую работу
- •3.2 Порядок выполнения работы
- •3.3 Проверка соответствия статистического распределения теоретическому по критерию Пирсона (æ²)
- •3.4 Проверка соответствия статистического распределения теоретическому по критерию Колмогорова (n)
- •Статистическое, 2- теоретическое;
- •Список рекомендованной литературы
- •Приложение а Справочные таблицы для проверки адекватности математических моделей
- •Приложение б Пример выполнения расчетно-графической работы
- •84313, М. Краматорськ, вул. Шкадінова, 72
2.4.1 Содержание и порядок выполнения работы
1 Строят матрицу полного факторного эксперимента (ПФЭ) в соответствии с общими правилами построения матриц.
2 Для удобства расчётов строят таблицу 2.11.
Таблица 2.11 – Исходные данные и результаты расчёта математической модели
Точка плана V |
Текущие значения параметра оптимизации |
Среднее значение уV |
Дисперсия опыта
|
Значения по модели |
Дисперсия
адекват-ности ( |
||||||
у1 |
у2 |
у3 |
|||||||||
1 |
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
||||
3 |
|
|
|
|
|
|
|
||||
4 |
|
|
|
|
|
|
|
||||
… |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
3 Уравнение регрессии записывают в виде
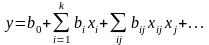 ,
(2.37)
,
(2.37)
где 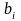 – коэффициент регрессии;
– коэффициент регрессии;
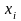 – независимые переменные.
– независимые переменные.
Коэффициенты регрессии рассчитывают по формуле
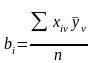 ,
(2.38)
,
(2.38)
где 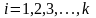 – номер фактора;
– номер фактора;
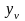 – среднее значение параметра оптимизации,
полученное по результатам эксперимента;
– среднее значение параметра оптимизации,
полученное по результатам эксперимента;
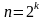 – минимальное
количество опытов.
– минимальное
количество опытов.
4 Определяют дисперсию, которая характеризует ошибку опыта
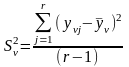 ,
(2.39)
,
(2.39)
где 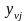 – текущее значение параметра оптимизации
(у1,
у2,
у3);
– текущее значение параметра оптимизации
(у1,
у2,
у3);
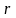 – число повторных опытов в каждой
строчке матрицы ПФЭ.
– число повторных опытов в каждой
строчке матрицы ПФЭ.
Значения
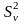 записывают в таблицу 2.11.
записывают в таблицу 2.11.
5 Определяют дисперсию параметра оптимизации, которая является средним арифметическим из дисперсии различных вариантов исследований
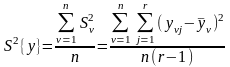 .
(2.40)
.
(2.40)
6
Выполняют проверку однородности
дисперсий по критерию
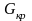 Кохрена. Критерий Кохрена – это отношение
максимальной дисперсии к сумме всех
дисперсий
Кохрена. Критерий Кохрена – это отношение
максимальной дисперсии к сумме всех
дисперсий
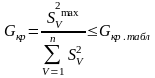 ,
(2.41)
,
(2.41)
где 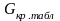 – табличные значения критерия Кохрена,
которые приведены в таблице А1 (Приложение
А).
– табличные значения критерия Кохрена,
которые приведены в таблице А1 (Приложение
А).
В
соответствии с таблицей для числа
степеней свободы числителя
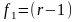 и знаменателя
и знаменателя
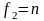 определяют
.
Дисперсии считают однородными, если
экспериментальные значения критерия
Кохрена не превышают табличных
определяют
.
Дисперсии считают однородными, если
экспериментальные значения критерия
Кохрена не превышают табличных
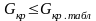 .
.
7 Рассчитывают дисперсию коэффициента регрессии
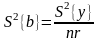 .
(2.42)
.
(2.42)
8 Проверяют значимость коэффициентов регрессии по критерию Стьюдента
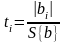 .
(2.43)
.
(2.43)
Расчётные
значения
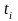 сравнивают
с табличными
сравнивают
с табличными
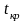 ,
которые выбирают при заданном уровне
значимости
,
которые выбирают при заданном уровне
значимости
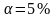 и числе степеней свободы
и числе степеней свободы
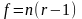 (таблица А2 (Приложение А)). Если
(таблица А2 (Приложение А)). Если
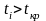 ,
то коэффициент считают значимым, в
противном случае – не значимыми.
,
то коэффициент считают значимым, в
противном случае – не значимыми.
9
Рассчитывают значения
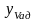 .
Для этого используют значимые коэффициенты
уравнения регрессии т соответствующие
номеру опыта строки матрицы ПФЭ. Значения
записывают в таблицу 2.11.
.
Для этого используют значимые коэффициенты
уравнения регрессии т соответствующие
номеру опыта строки матрицы ПФЭ. Значения
записывают в таблицу 2.11.
10 Рассчитывают дисперсию адекватности
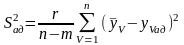 ,
(2.44)
,
(2.44)
где m –число значимых коэффициентов уравнения регрессии.
11 Проверяют адекватность полученной математической модели по критерию Фишера
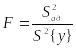 .
(2.45)
.
(2.45)
Если
расчётные значения
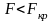 ,
то считают, что полученная математическая
модель адекватна, значения
,
то считают, что полученная математическая
модель адекватна, значения
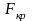 выбирают при уровне значимости
,
числе степеней свободы числителя
выбирают при уровне значимости
,
числе степеней свободы числителя
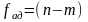 и числе степеней свободы знаменателя
и числе степеней свободы знаменателя
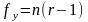 (таблица А3) (Приложение А).
(таблица А3) (Приложение А).
Если
отношение
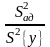 меньше единицы, то условие
выполняется для любого числа степеней
свободы.
меньше единицы, то условие
выполняется для любого числа степеней
свободы.

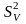
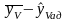 )2
)2