2.2.1 Содержание и порядок выполнения работы

1 Статистическую оценку показателей надежности инструмента (вероятностных эксплуатационных характеристик) осуществляют по результатам его испытаний. Для периода стойкости строят вариационный ряд (значения периода стойкости располагают в порядке возрастания). Значения заносят в таблицу 2.2.

Таблица 2.2 – Вариационный ряд периода стойкости инструмента

№№ п/п	1	2	3	…	n-2	n-1	n
				…

2 Вариационный ряд разбивают на интервалы. Число интервалов рассчитывают по формуле

, (2.21)

где n – объем испытаний (число исходных данных).

3 Определяют среднее значение периода стойкости

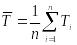, (2.22)

где - текущие значения периода стойкости.

4 Рассчитывают среднее квадратичное отклонение периода стойкости

. (2.23)

5 Рассчитывают коэффициент вариации периода стойкости

. (2.24)

6 Для предварительного определения закона распределения периода стойкости используют расчетные значения коэффициентов вариации (таблица 2.3)

Таблица 2.3 – Выбор закона распределения периода стойкости

Коэффициент вариации	Закон распределения
	Нормальный
	Вейбулла-Гнеденко
	Экспоненциальный

7 Основными показателями надежности режущего инструмента являются: плотность распределения периода стойкости , вероятность безотказной работы и интенсивность отказов . Значения этих показателей рассчитывают для интервалов времени от до

, (2.25)

где - величина интервала.

, (2.26)

где - минимальное значение периода стойкости в вариационном ряду;

- максимальное значение периода стойкости в вариационном ряду;

- количество интервалов.

8 Плотность распределения периода стойкости определяют по формуле

, (2.27)

где - число отказов инструмента в интервале времени от до .

9 Вероятность безотказной работы определяют по формуле

. (2.28)

10 Интенсивность отказов (вероятность отказа в единицу времени Т при условии, что до этого времени отказ не возник) определяют по формуле

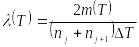, (2.29)

где - число инструментов, работающих соответственно в начале и в конце -го интервала времени .

11 По результатам расчета строят графики. Результаты расчета заносят в таблицу 2.4.