1.3.3. Пример построения многофакторной линейной модели в Excel

1 Настройка пакета анализа

См. п.1.3.1.

2 Ввод данных

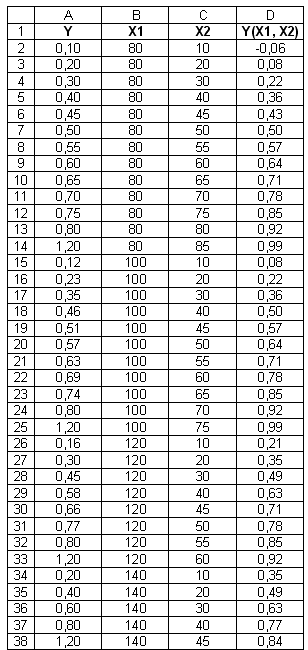
Исходные данные вводятся на рабочий лист пакета Excel (табл. 1.24).

Таблица 1.24 - Исходные данные для получения модели

3 Нахождение основных числовых характеристик

Чтобы найти основные числовые характеристики, выбираем пункт меню Сервис – Анализ данных – Описательная статистика (см. 1.3.1).

Получается следующая таблица для двухфакторной регрессии (таблица 1.25).

Таблица 1.25 – Основные числовые характеристики

	Y	X1	X2
Среднее	0,584324	102,7027	44,86486
Стандартная ошибка	0,04922	3,479857	3,479274
Медиана	0,58	100	45
Мода	0,8	80	10
Стандартное отклонение	0,299393	21,16715	21,1636
Дисперсия выборки	0,089636	448,048	447,8979
Эксцесс	-0,00364	-1,0036	-0,85855
Асимметричность	0,50836	0,459765	-0,06146
Интервал	1,1	60	75
Минимум	0,1	80	10
Максимум	1,2	140	85
Сумма	21,62	3800	1660
Счет	37	37	37

4 Нахождение параметров линейной регрессии

Чтобы найти параметры регрессии, выбираем пункт меню Сервис – Анализ данных – Регрессия. Здесь задаем диапазоны отдельно для Y, отдельно – для X (для двухфакторной регрессии в поле «Входной интервал Х» выделяем все значения Х1 и Х2), устанавливаем флажок в окошке «Метки», «Остатки», «Выходной диапазон» – на новый лист. Ок.

Результат получаем в виде нескольких таблиц (1.26…1.29).

Таблица 1.26 – Регрессионная статистика

Множественный R	0,922267101
R-квадрат	0,850576606
Нормированный R-квадрат	0,841786995
Стандартная ошибка	0,119086667
Наблюдения	37

Таблица 1.27 – Дисперсионный анализ

	df	SS	MS	F	Значимость F
Регрессия	2	2,744732547	1,372366273	96,77067242	9,2281Е-15
Остаток	34	0,482175561	0,014181634
Итого	36	3,226908108

Таблица 1.28 – Коэффициенты модели

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,75088824	0,130300871	-5,762730	1,75Е-06	-1,015692	0,486085
Х1 Х2	0,006869311 0,014035845	0,001015348 0,001015518	6,765475 13,821363	8,88Е-08 1,63Е-15	0,004805 0,011972	0,008933 0,017001

Здесь Множественный R = 0,922, что свидетельствует о тесной взаимосвязи между откликом Y факторами X1, X2. R-квадрат = 0,85 (85%) – значит, общее качество модели хорошее; стандартная ошибка = 0,119.

Значимость F = 9,228E-15 = 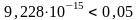, что означает, что полученная модель адекватна по критерию Фишера исходным данным с заданным уровнем доверия. Все дальнейшие расчеты выполняются только при условии адекватности модели.

Коэффициенты линейной модели , , . Оба коэффициента статистически значимы по критерию Стьюдента, т. к. для P-Значение = , для P-Значение = , для P-Значение = .

Полученная линейная двухфакторная модель .