2.3.5.2. Методы, основанные на использовании преобразования Лапласа
В общем случае согласно определению передаточной функции (см.(2.13)) справедливо соотношение
что позволяет определить формулы для вычисления изображений временных характеристик.
а)
(2.31)
б)
(2.32)
Если задана передаточная функция
,
то, используя обратное преобразование
Лапласа, определяются функции
и
.
Самым универсальным является метод,
основный на применении теоремы о
вычетах.
Пусть известны корни характеристического
уравнения (2.15)
.
Тогда аналогично формуле (2.16) справедливо
соотношение
(2.33)
Применяя обратное преобразование Лапласа, получим выражение, совпадающее с (2.26)
. (2.34)
При разложении изображения
появляется дополнительный нулевой
корень
его характеристического уравнения
.
Таким образом,
2.3.5.3. Моделирование сау
Определение временных характеристик с применением описанных выше методов, если и возможно, то весьма трудоемко даже для систем невысокого порядка. Поэтому широко используется моделирование систем: аналоговое или цифровое, наиболее распространенное в последнее время. Различают два вида моделирования: структурное и абстрактное.
а) Структурное моделирование.
Состав и закон изменения машинных переменных модели непосредственно совпадают с составом и законом изменения физических переменных, отличающихся только масштабными коэффициентами.
б) Абстрактное моделирование.
Для упрощения математического описания системы производится замена физических переменных системы некоторыми абстрактными. С участием абстрактных переменных формируется аналоговая или цифровая модель. Примером абстрактной математической модели является описание системы дифференциальными уравнениями.
2.4 Типовые звенья
В предыдущем разделе было показано, что любая передаточная функция может быть представлена как произведение передаточных функций типовых звеньев (см. (2.19)). Это обстоятельство в ряде случаев позволяет существенно упростить расчеты, связанные с анализом и проектированием линейных систем. В данном разделе будут рассмотрены наиболее значимые характеристики типовых звеньев.
Идеальное усилительное звено.
k – безразмерный
коэффициент усиления. (2.37)
АФХ звена вырождается в точку с координатой (k,0) на вещественной оси комплексной плоскости.
ЛАХ звена: L(ω) = 20lg(k) = const, ϕ(ω) = 0.
График функции L= L(ω) – прямая, параллельная оси частот, проходящая на уровне 20lg(k) ; график функции ϕ = ϕ(ω) совпадает с осью частот.
2.4.2 Идеальное интегрирующее звено.
, (2.38)
где k – коэффициент
усиления, его размерность [k]
=
(радиан в секунду),
T – постоянная времени звена, [T] = с.
Комплексный коэффициент передачи звена
,
. (2.39)
,
,
. (2.40)
Согласно выражению (2.39) годограф
комплексного коэффициента передачи
инерционного звена совпадает с
отрицательной частью мнимой оси. Когда
частота ω = 0 его амплитуда бесконечна,
с увеличением частоты она уменьшается
и при
годограф приходит в начало координат.
График L = L() логарифмической амплитудно-частотной характеристики интегрирующего звена (учитывая логарифмический масштаб по оси ) представляет собой прямую с наклоном – 20 дБ/дек во всей области частот (0 <), пересекающую ось на частоте = k. (Наклон -20 дБ/дек означает, что при увеличении частоты в 10 раз (на декаду) величина L() уменьшится на 20 дБ).
Логарифмическая фазочастотная характеристика во всей области частот равна () – 90. На рис. 2.5 точно один под другим изображены графики ЛАХ интегрирующего звена.
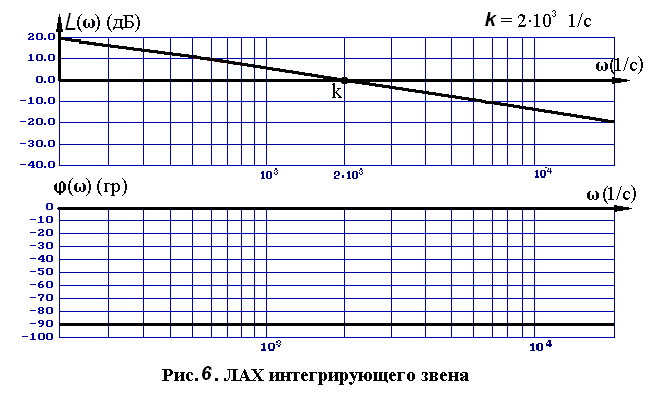
Рис. 2.5. ЛАХ идеального интегрирующего звена