§1.2. Системы m линейных алгебраических уравнений с m неизвестными

Система m линейных уравнений с m неизвестными имеет вид:

.

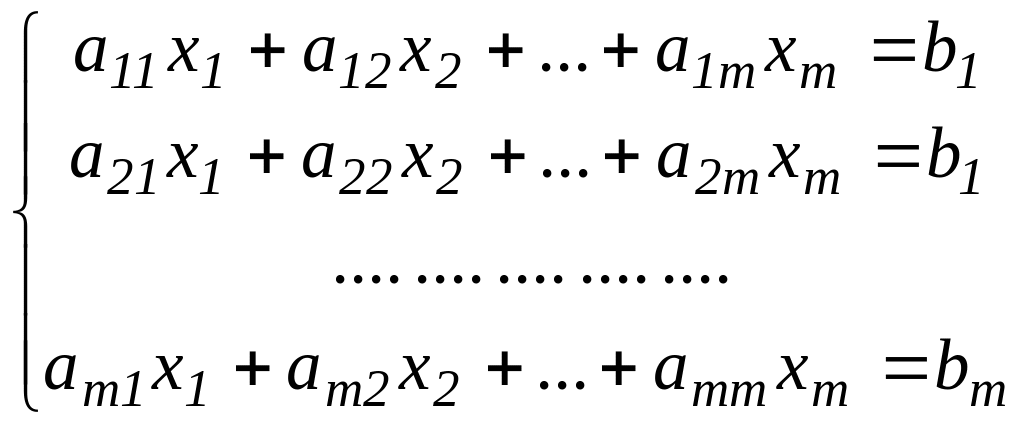Определитель, составленный из коэффициентов при неизвестных

,

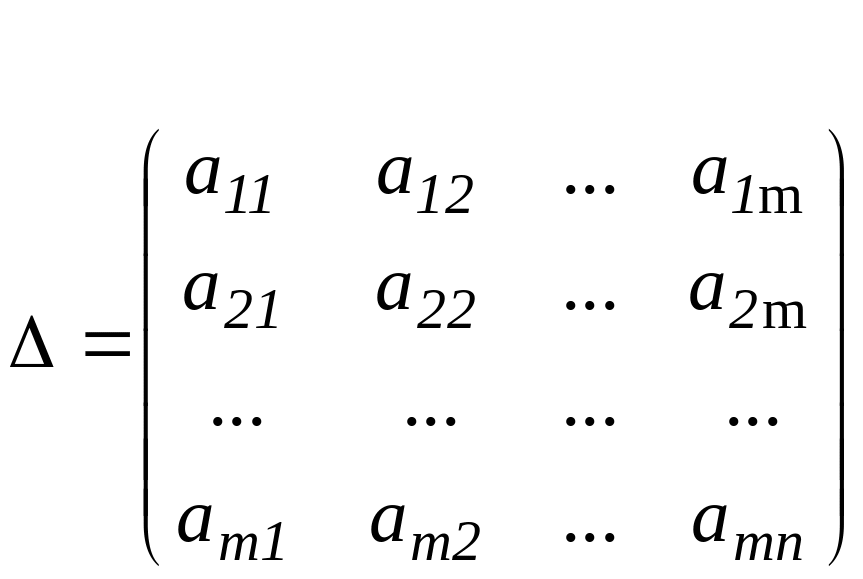называется главным определителем системы.

Если Δ≠0, то система имеет единственное решение, которое может быть найдено по правилу Крамера:

, где i=1,2,…, m.

Определители Δx_i получаются из главного определителя системы путем замещения элементов i-го столбца столбцом свободных членов.

Пример. Решить систему уравнений

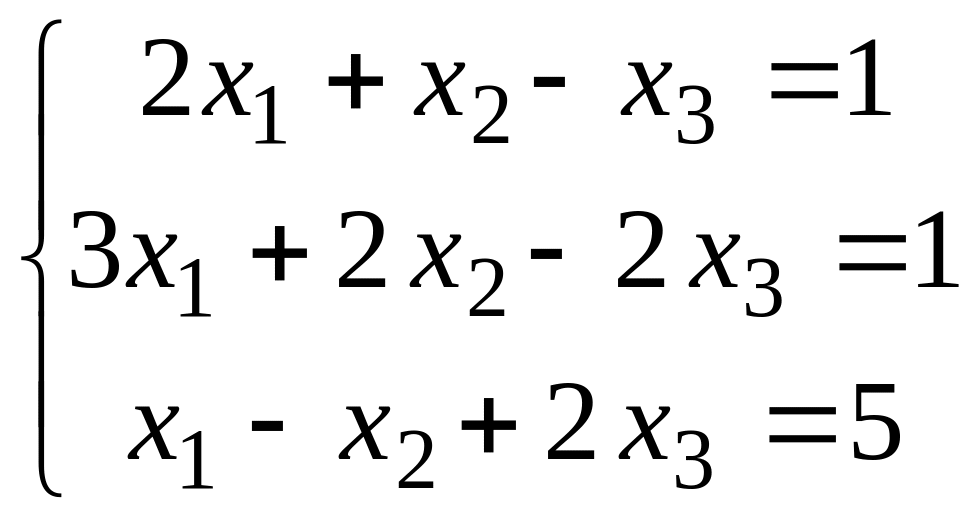. (1)

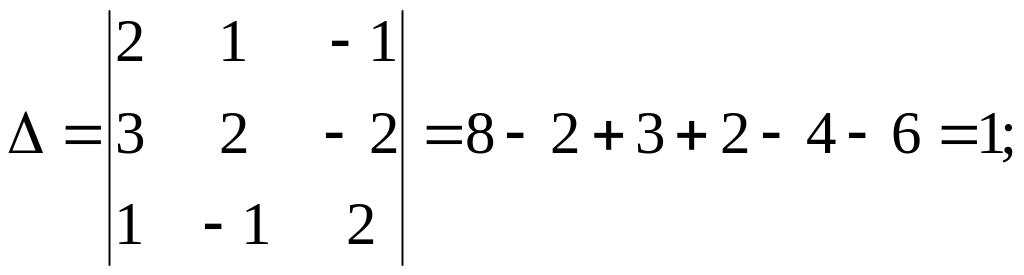
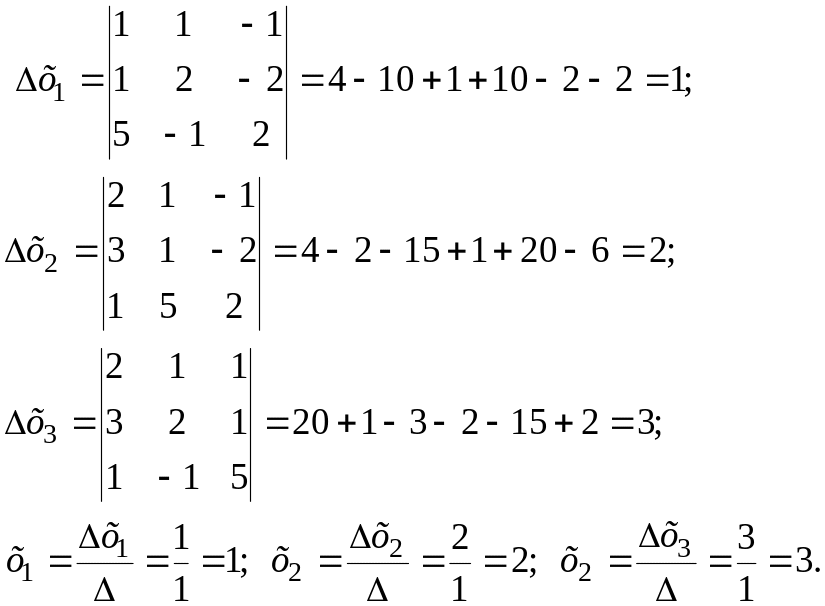
Другим способом решения систем линейных уравнений является метод Гаусса или метод исключения, который состоит из двух этапов. На первом этапе путем линейных преобразований уравнений системы заданная система приводится к ступенчатому, в частности, треугольному виду; на втором этапе определяются значения неизвестных. В качестве примера решим систему (1) методом Гаусса.

Разделим все члены первого уравнения системы (1) на коэффициент а₁₁=2. Получим систему

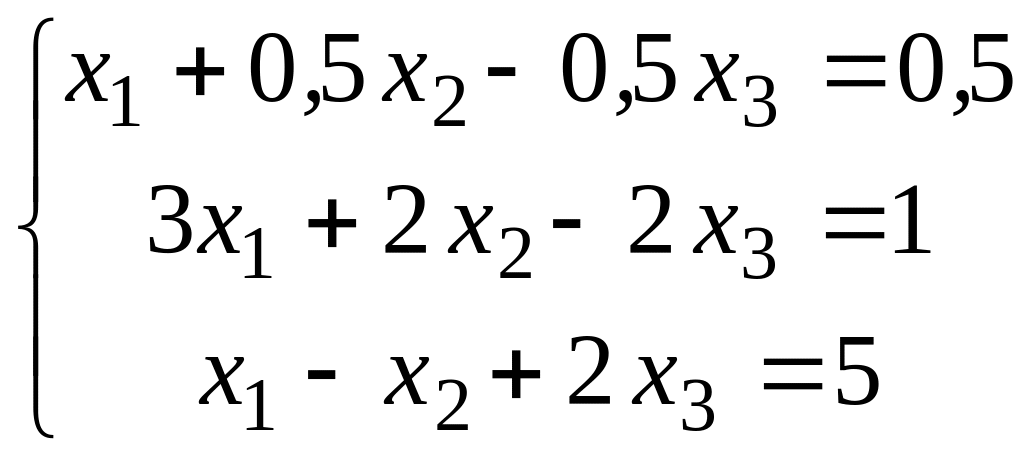. (2)

Умножим все члены первого уравнения на 3 и вычтем их из второго уравнения, затем из третьего уравнения вычтем первое, само первое уравнение системы (2) оставим без изменения. Тогда будем иметь

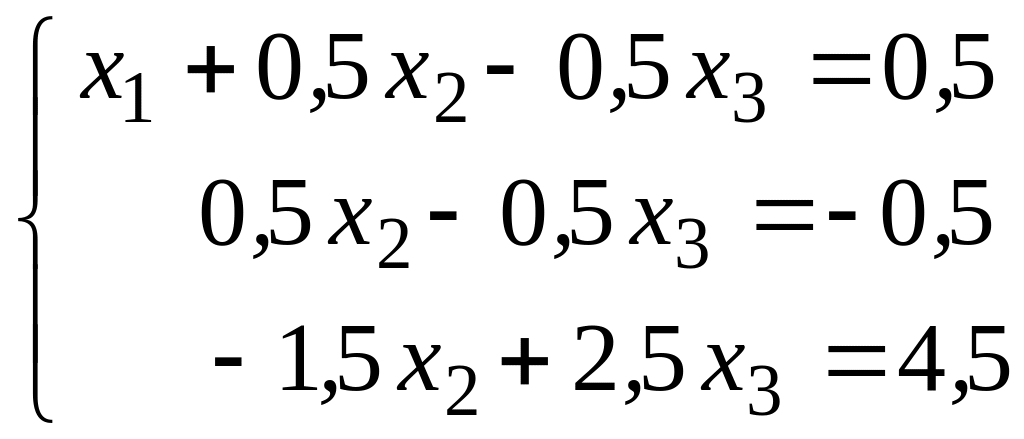. (3)

Разделим все члены второго уравнения на 0,5:

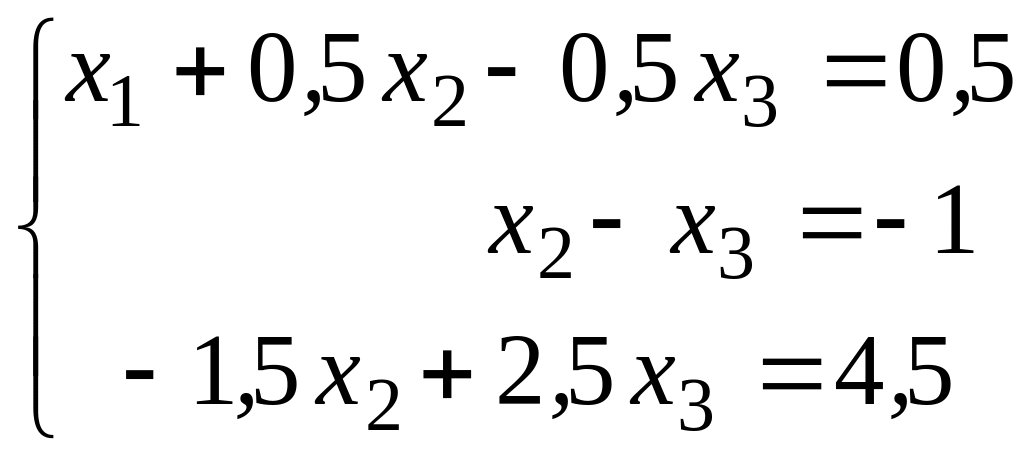. (4)

Умножим второе уравнение на -0,5 и вычтем его из третьего, при этом первое и второе уравнения системы (4) оставим без изменения

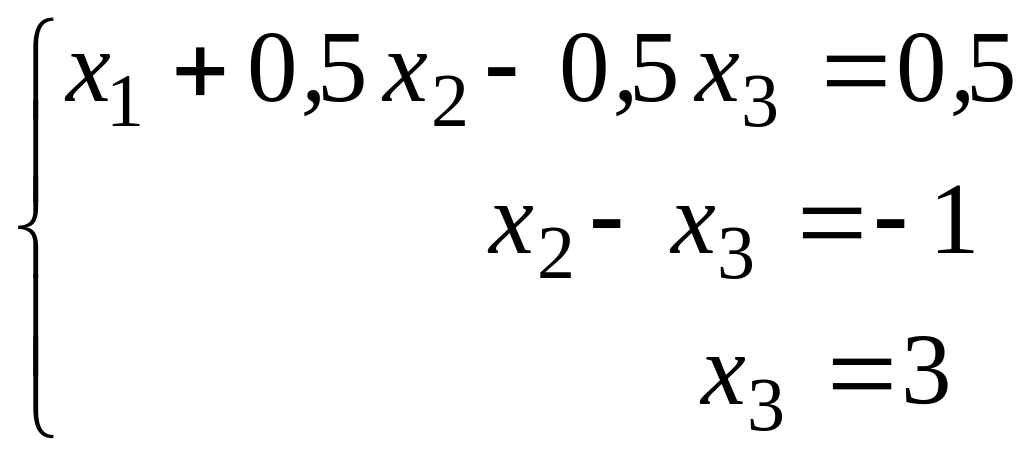. (5)

На этом завершен так называемый прямой ход метода Гаусса. Неизвестные находятся в обратной последовательности. Из последнего уравнения находим х₃=3, из второго следует х₂, из первого х₁=0,5-0,5∙2+0,5∙3=1.

Замечания. Следует иметь в виду, что если главный определитель системы Δ≠0, то система имеет единственное решение. Если Δ=0, но хотя бы один из определителей Δх_i ≠0, то система не имеет решений. Если Δ=0 и все определители Δх_i =0, то система имеет бесчисленное множество решений.

______________

1.2.1. Решить системы уравнений по правилу Крамера:

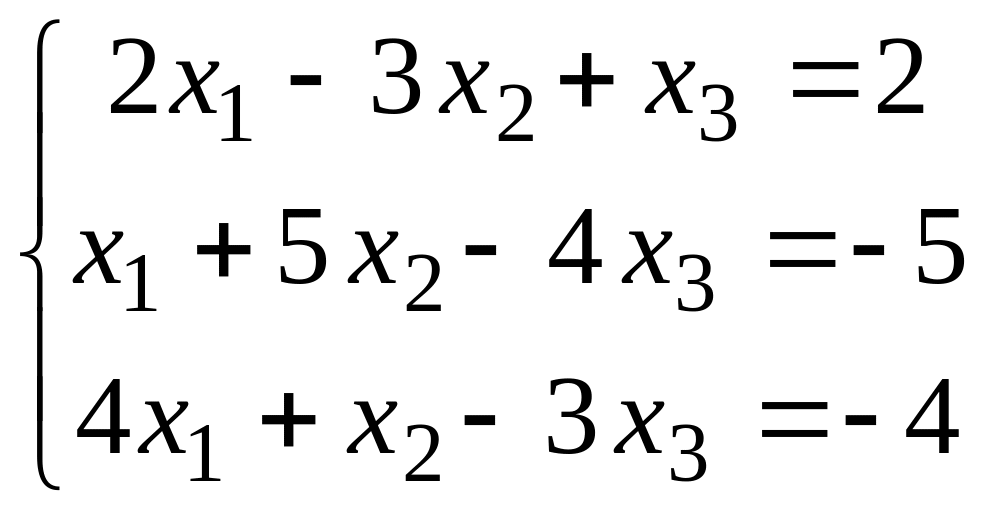а) ; б) ; в) .

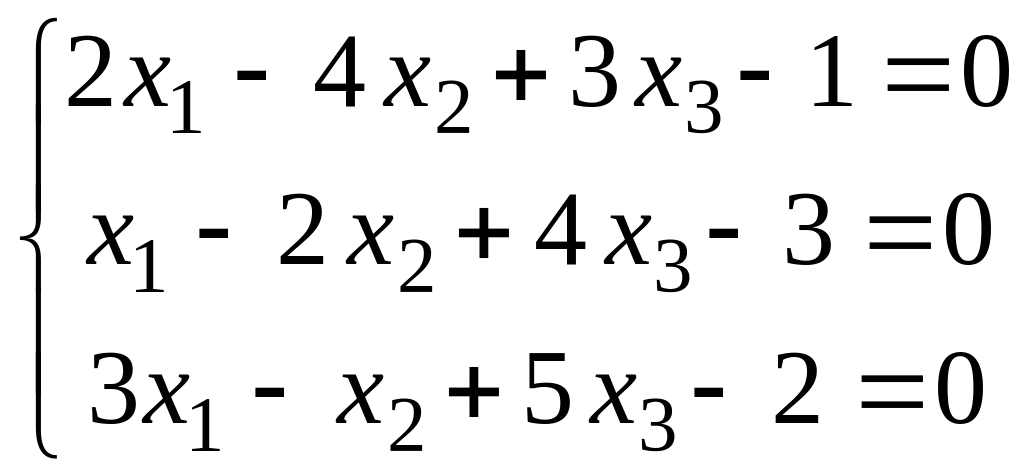1.2.2. Решить систему уравнений двумя способами: по правилу Крамера и методом Гаусса.

.

1.2.3. Решить системы уравнений методом Гаусса

а) 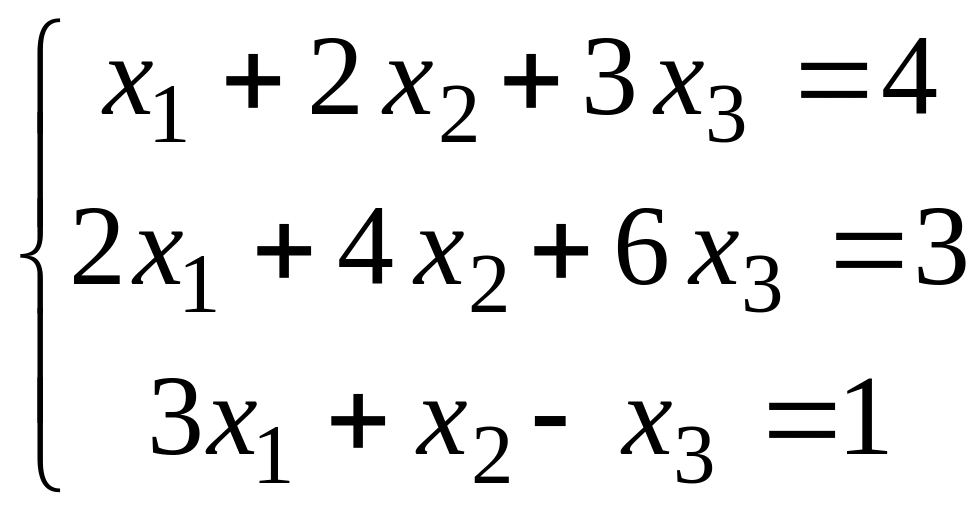; б) ;

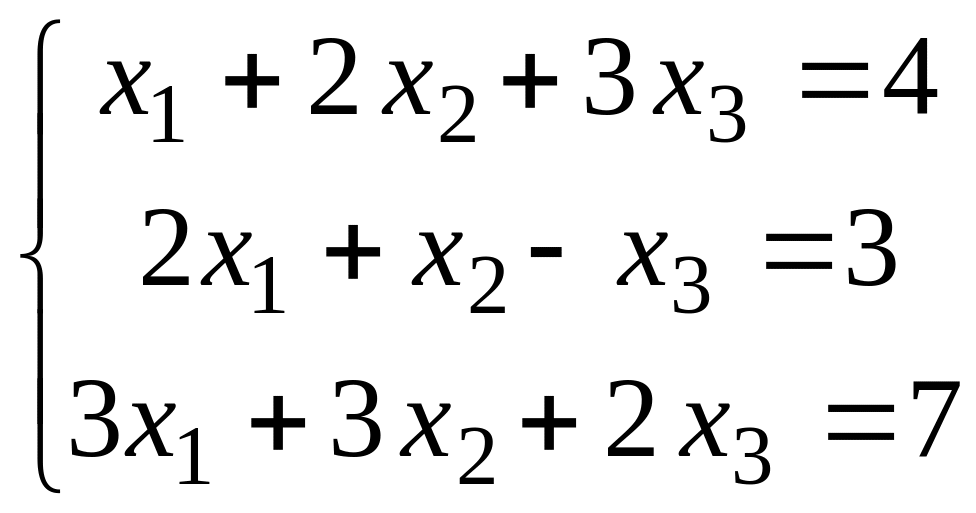в) .

____________

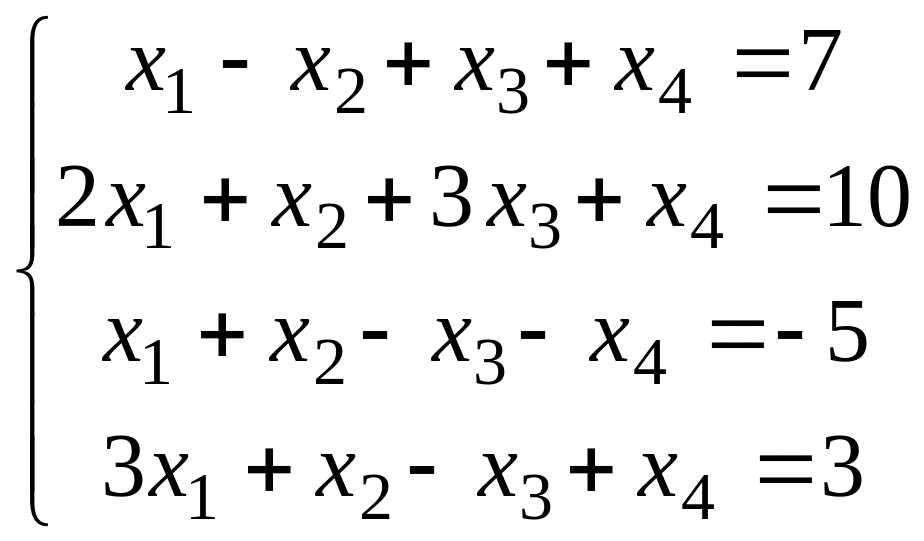1.2.4. Решить системы уравнений по правилу Крамера

а) ; б) .

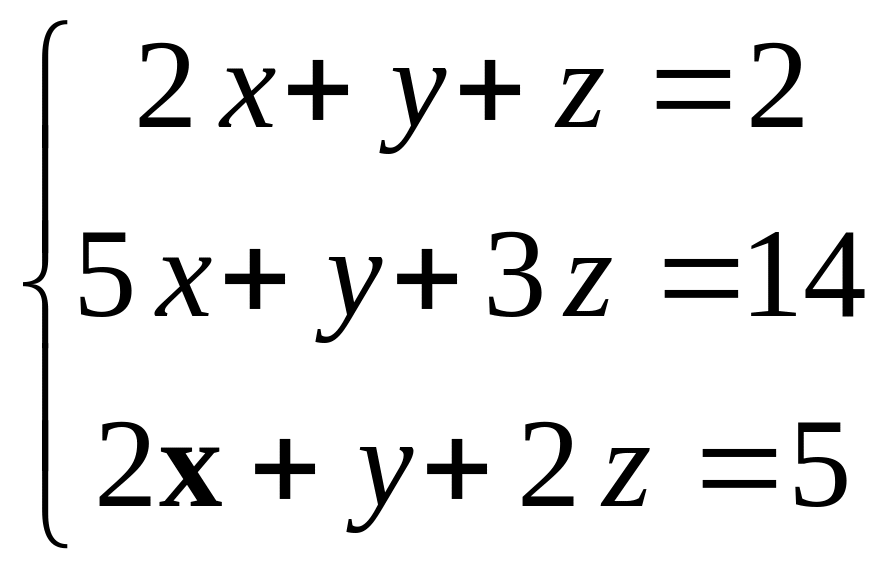1.2.5. Решить систему уравнений двумя способами

.

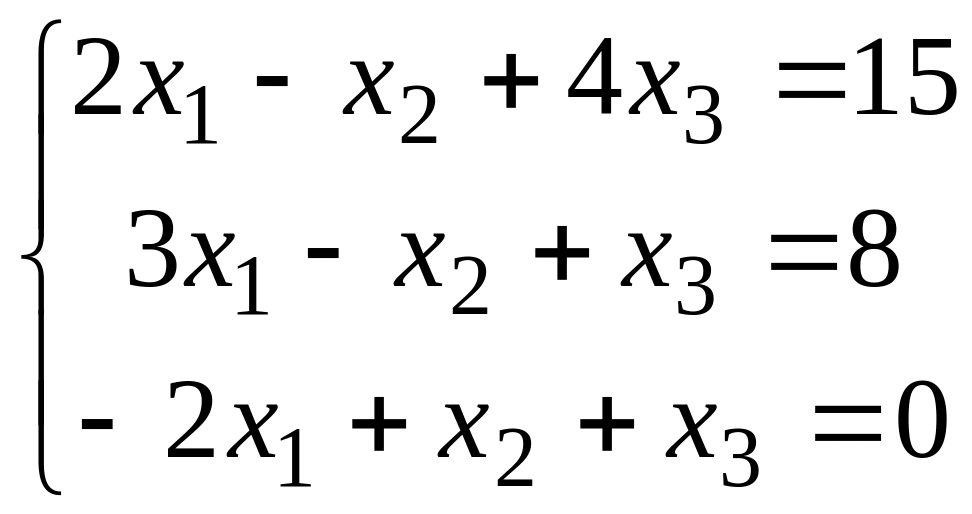1.2.6. Решить систему методом Гаусса

.

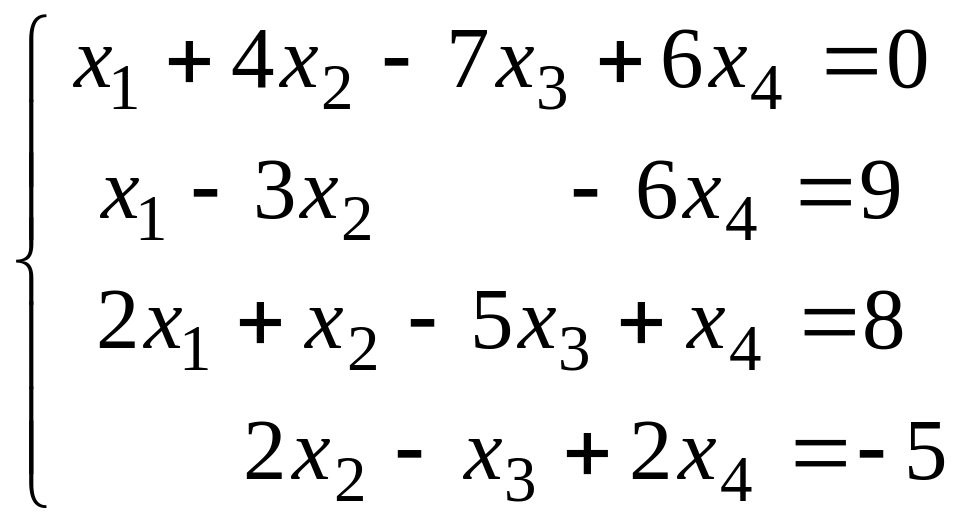1.3. Операции над матрицами

Суммой матриц А = (a_ij) и В = (b_ij) одинакового размера называется матрица С = (с_ij) того же размера, причем с_ij= a_ij + b_ij, i,j.

Свойства операции сложения матриц

Для любых матриц А, В и С одного размера выполняются равенства:

1. А+В=В+А (коммутативность);

2. (А+В)+С=А+(В+С)=А+В+С (ассоциативность).

Произведением матрицы А = (a_ij) на число  называется матрица В = (b_ij) того же размера, что и матрица А, причем b_ij= a_ij, i,j.

Свойства операции умножения матрицы на число

1. (А)=()А (ассоциативность).

2. (А+В)=А+В (дистрибутивность относительно сложения матриц).

3. (+)А=А+А (дистрибутивность относительно сложения чисел).

Произведением АВ матриц А и В (размеров mn и nr соответственно) называется матрица С размера mr, такая, что с_ij= a_i1 b_1j+ a₁₂ b_2j+…+ a_ik b_kj+…+ a_in b_nj= .

Таким образом, каждый элемент с_ij, находящийся в i-й строке и j-м столбце матрицы С, равен сумме произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В.

Получение элемента с_ij схематично изображается так

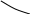
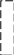
j

Произведение АВ существует, только если число столбцов матрицы А равно числу строк матрицы В.

Свойства операции умножения матриц

1. (АВ)С=А(ВС)=АВС (ассоциативность).

2. (А+В)С=АС+ВС (дистрибутивность).

3. А(В+С)=АВ+АС (дистрибутивность).

4. АВВА (отсутствует коммутативность).

Коммутирующими (или перестановочными) называются матрицы А и В, для которых АВ=ВА.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной (обозначается А^Т).

_________________

1.3.1. Найти линейные комбинации заданных матриц:

а) А-Е, ;

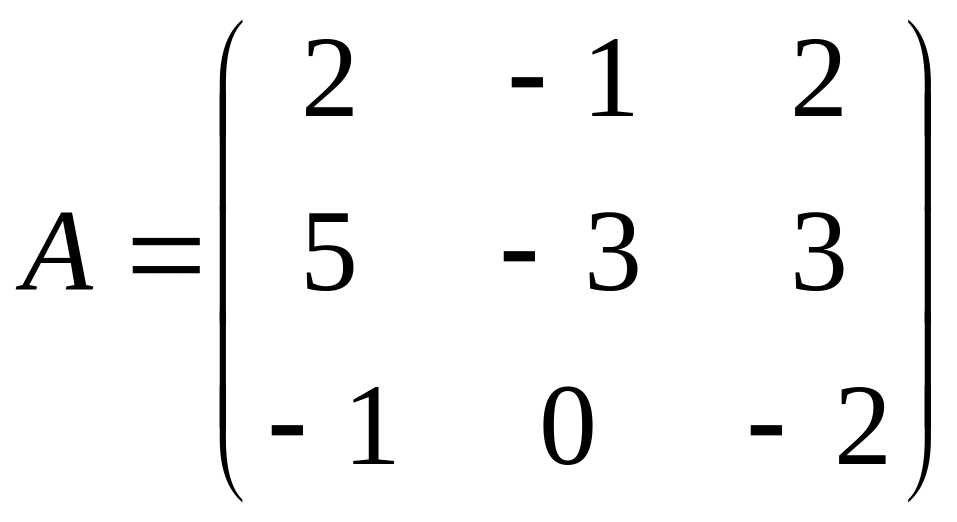б) 4А-5В, .

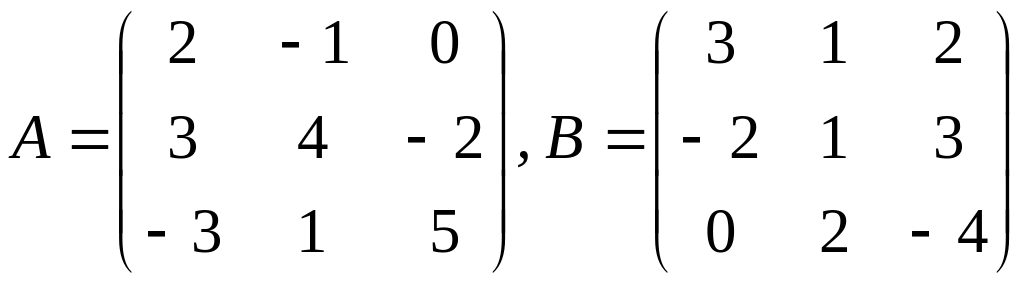1.3.2. Найти произведения матриц АВ и ВА (если они существуют):

а) ; б) А=(4 0 -2 3 1), ;

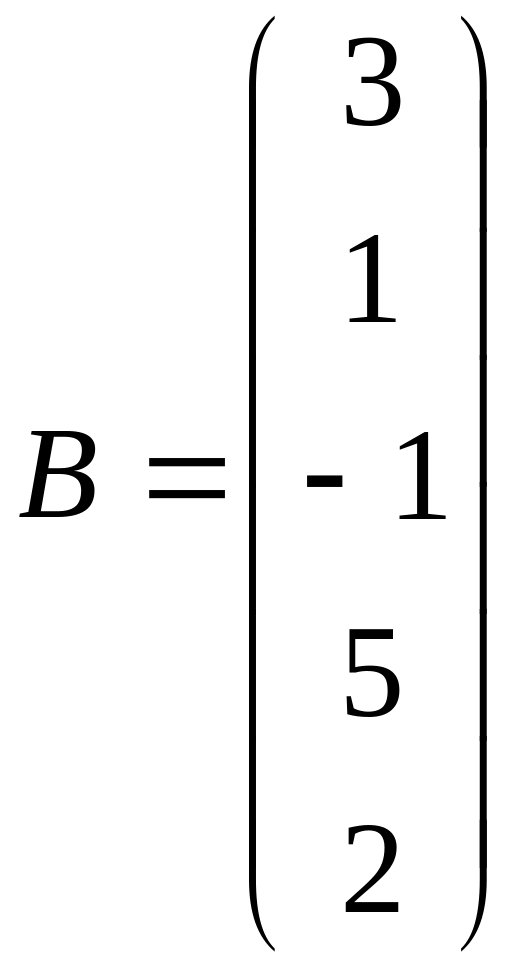в) .

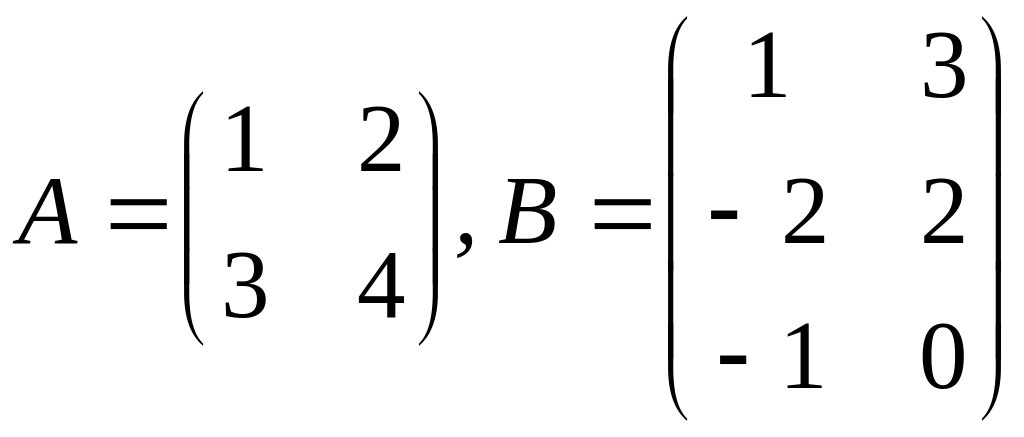1.3.3. Проверить, коммутируют ли матрицы:

а) ;

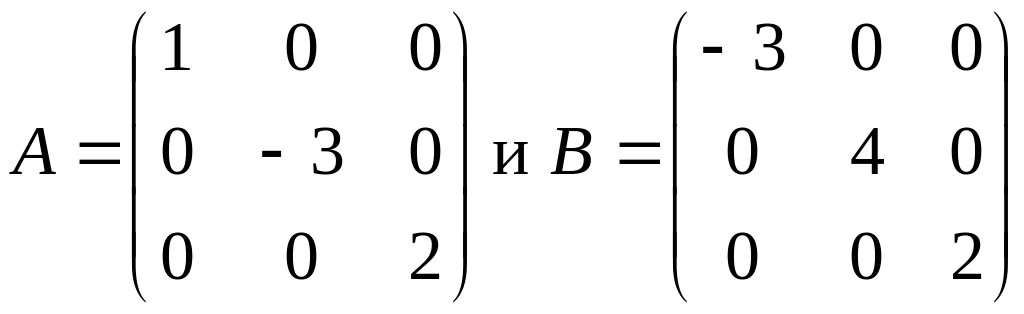б) .

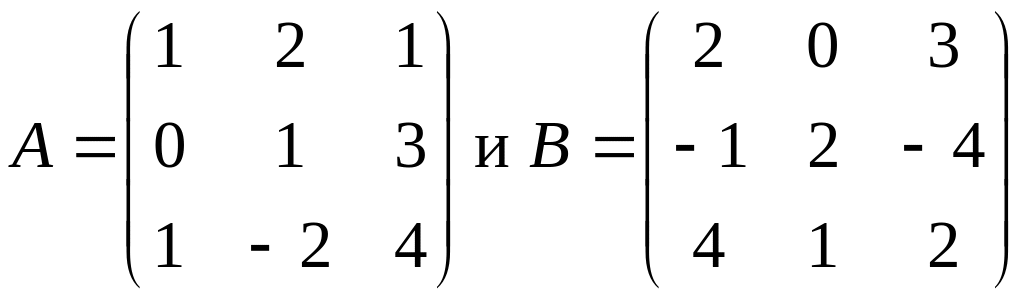1.3.4. Найти произведения матриц АА^Т и А^ТА:

а) б) А=(1 2 3 4); в) .

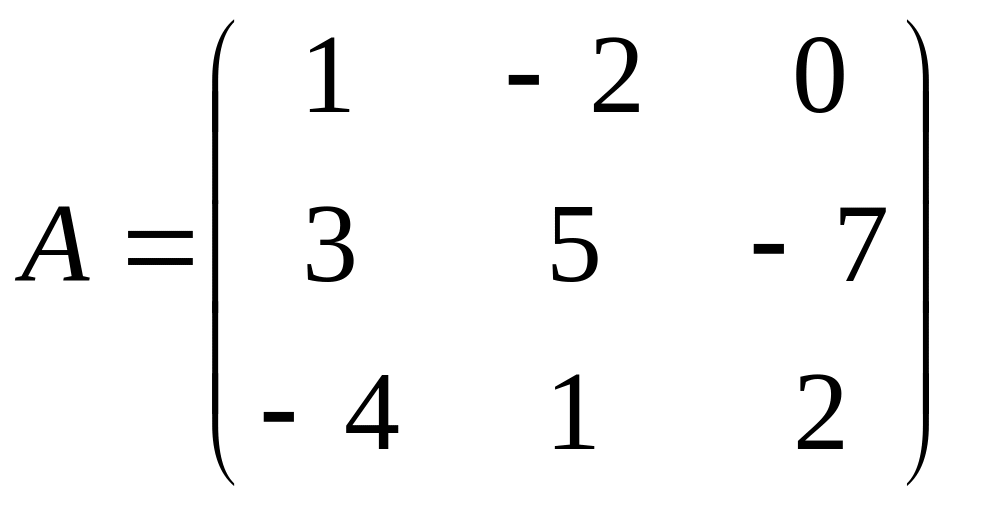1.3.5. Найти линейные комбинации матриц:

а) 5А-3В+2С, ;

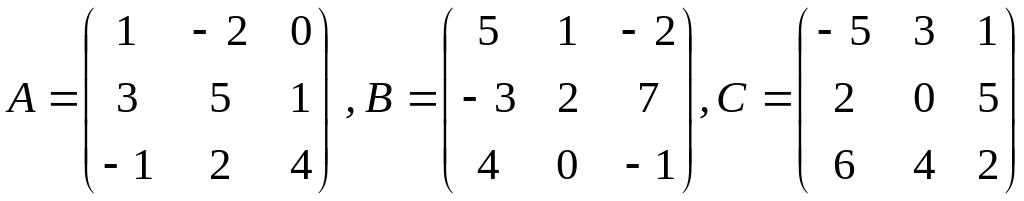б) А-Е, .

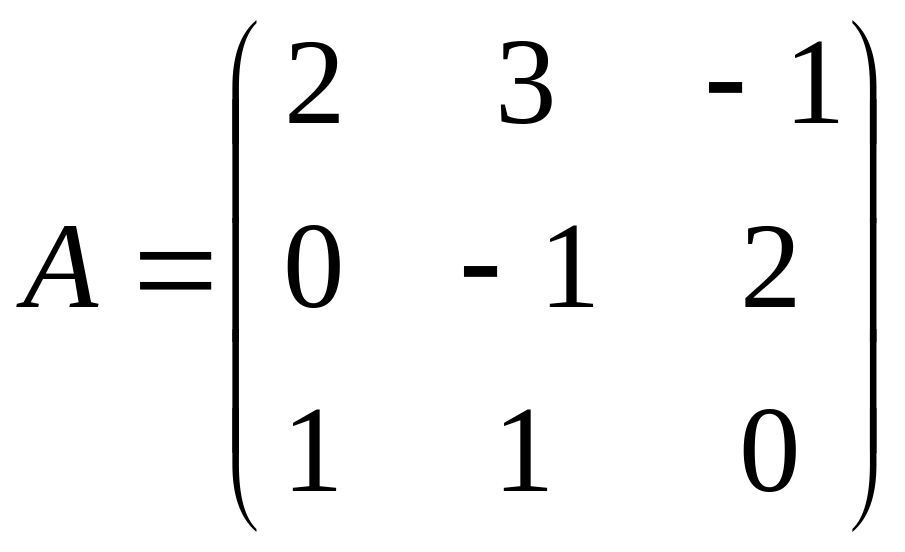1.3.6. Найти произведения АВ и ВА (если это возможно):

а) 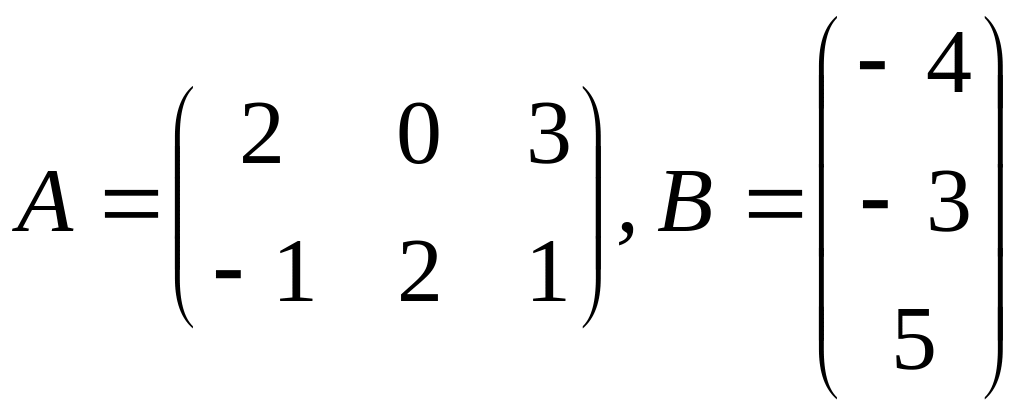; б) .

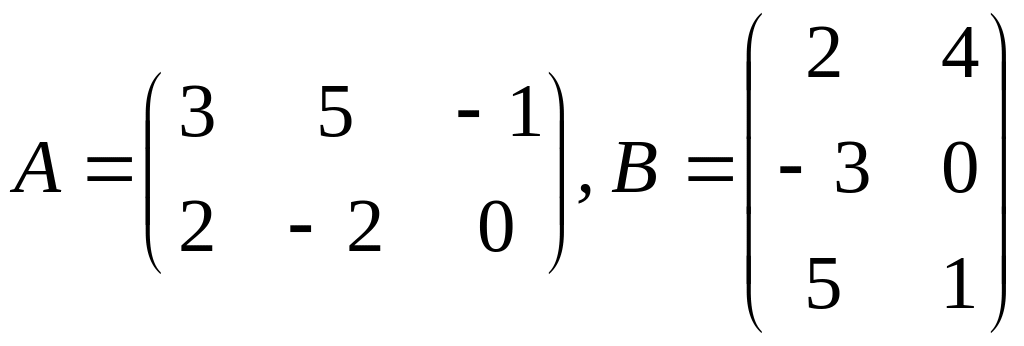1.3.7. Найти произведения АА^Т и А^ТА:

а) 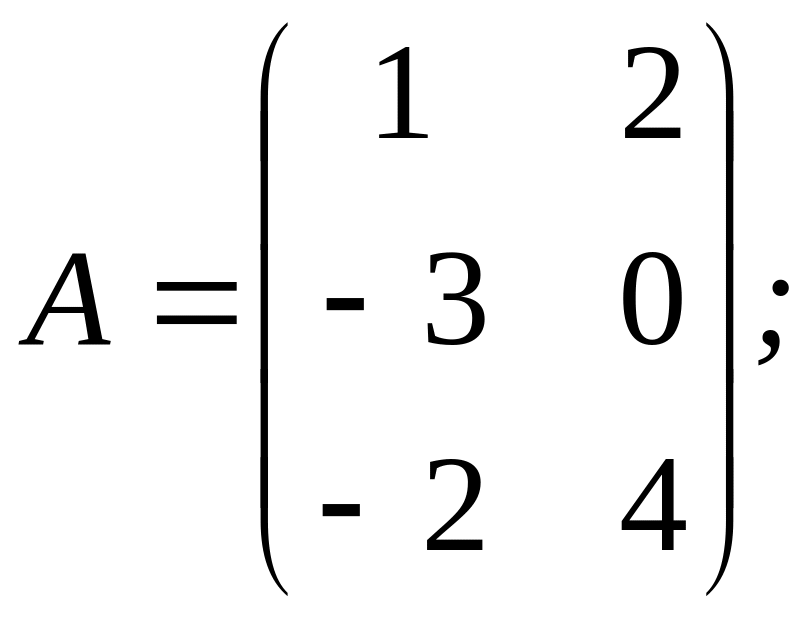б) .

________________________
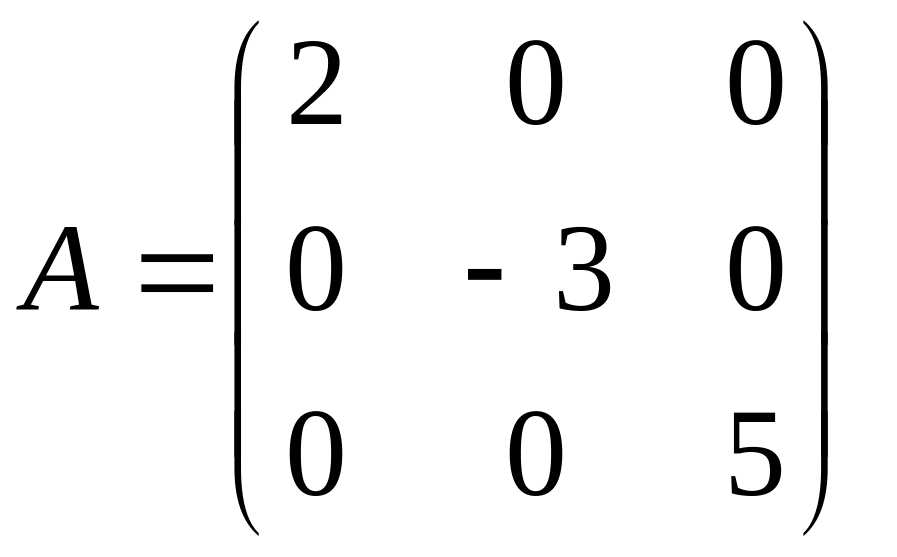