§4.7. Промежутки выпуклости, вогнутости графика функции. Точки перегиба. Асимптоты

Кривая называется выпуклой в точке х=х₀, если в некоторой окрестности этой точки кивая расположена под касательной, проведенной в этой точке (рис.6а), если же кривая лежит над касательной, то функция называется вогнутой (рис.6б).

В качестве достаточных условий выпуклости, вогнутости графика функций можно принять следующие: если y">0, то кривая вогнутая, если y"<0, то кривая выпуклая.

Точкой перегиба называется точка, разделяющая интервал выпуклости от интервала вогнутости. Необходимым условием существования точки перегиба является равенство нулю второй производной от функции, достаточным – изменение знака второй производной при переходе через точку, подозрительную на точку перегиба.

Пусть имеется кривая, ветвь которой в том или ином направлении удаляется в бесконечность. Если расстояние от точки кривой до некоторой прямой по мере удаления точки кривой в бесконечность стремится к нулю, то эта прямая называется асимптотой графика кривой.

Существует три вида асимптот: вертикальная, горизонтальная, наклонная.

Пусть y=f(x), а – точка разрыва функции или граничная точка области определения.

Если , то прямая х=а есть вертикальная асимптота.

Если , то прямая х=b – горизонтальная асимптота.

Наклонная асимптота имеет вид у=kx+b, где ; .

Замечание. Пределы при х∞, х-∞ находятся отдельно.

Алгоритм полного исследования функции y=f(x)

1. Найти область определения функции; точки разрыва.

2. Найти асимптоты графика функции.

3. Определить четность, нечетность, периодичность функции.

4. Установить промежутки возрастания, убывания и экстремумы функции.

5. Определить интервалы выпуклости, вогнутости и точки перегиба графика функции.

6. Найти точки пересечения графика с осями координат.

7. При необходимости вычислить значения функции в дополнительных точках.

___________________

4.7.1. Найти промежутки выпуклости, вогнутости, точки перегиба:

а) у=х⁵-5х-6; б) у=(х-5)^5/3+2;

в) у=хе^х; г) у=х⁴-8х³+24х².

4.7.2. Найти асимптоты графика функций:

а) ; б) ;

в) ; г) y=-xarctgx.

4.7.3. Исследовать функции и построить их графики:

а) ; б) ;

в) ; г) .

4.7.4. Найти промежутки выпуклости, вогнутости, точки перегиба:

а) ; б) ;

в) y=ln|x|; г) .

4.7.8. Найти асимптоты графиков функций:

а) ; б) y=x-arctgx;

в) .

4.7.9. Исследовать функции и построить графики:

а) ; б) .

§4.8. Параметрически заданные функции. Векторная функция скалярного аргумента. Кривизна плоской кривой

Пусть даны две функции переменной величины , рассматриваемые для одних и тех же значений t. Эти уравнения на плоскости задают некоторую кривую. Так как переменная t называется параметром, то и приведенная система называется параметрическим уравнением кривой.

Если , то , а .

Пусть теперь некоторая кривая задана в пространстве R₃ своими параметрическими уравнениями: 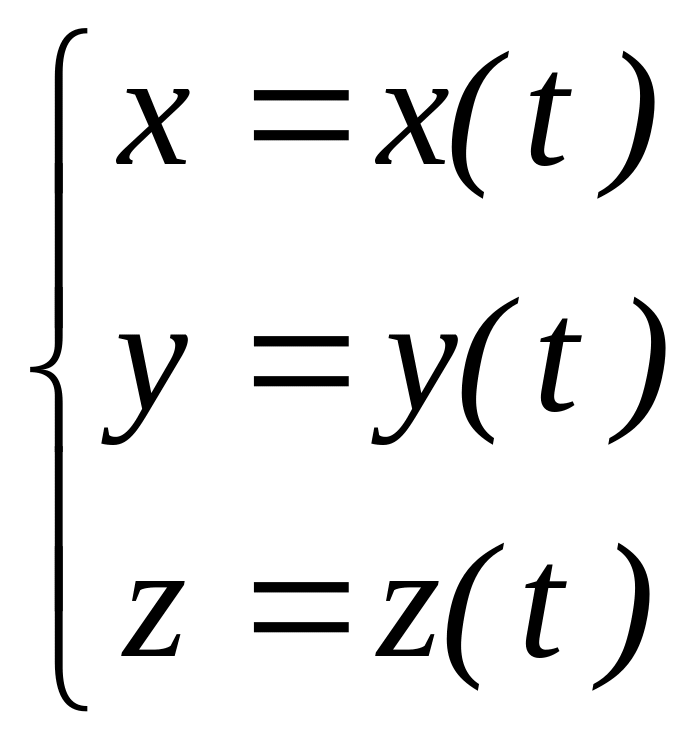. Тогда каждому значению t можно поставить в соответствие вектор , который называется векторной функцией скалярного аргумента t. Линия с, описываемая концом радиуса – вектора , называется годографом.

Если рассматривать как траекторию движения материальной точки в пространстве, то законы изменения скорости и ускорения движения этой точки имеют вид:

Пусть задана плоская кривая уравнением y=f(x). Величина определяет ее кривизну.

Радиус кривизны есть . Для параметрически заданной кривой .

________________

4.8.1. Найти , если x=arccost, y=arcsint.

4.8.2. Исключить параметр t из уравнений x=acost, y=bsint. Построить кривую.

4.8.3. Траектория движения материальной точки задана уравнением . Найти закон изменения скорости движения. Построить траекторию и векторы скорости при t=0; t=1.

4.8.4. Определить кривизну кривой 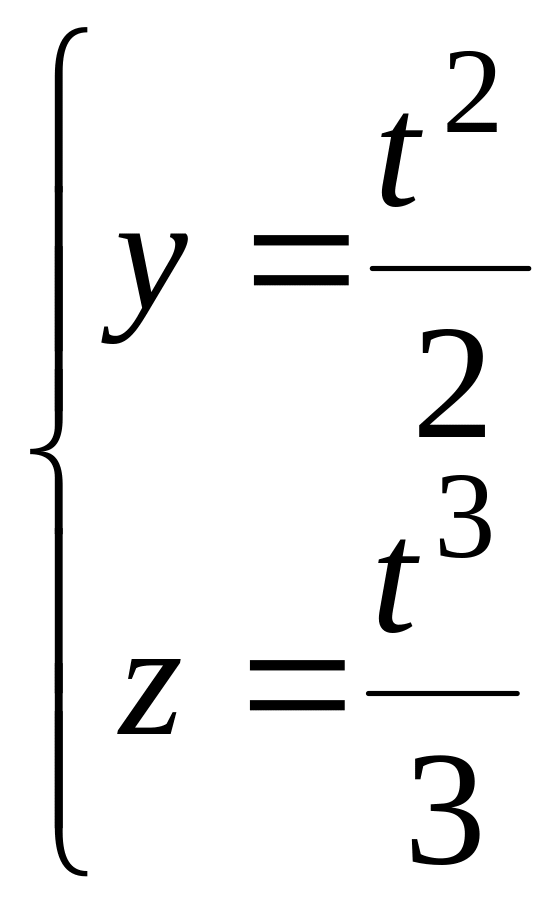при t=1.