
- •Высшая математика
- •Содержание
- •Глава I. Элементы линейной алгебры
- •§1.1. Матрицы и определители
- •§1.2. Системы m линейных алгебраических уравнений с m неизвестными
- •1.3. Операции над матрицами
- •1.4. Обратная матрица. Матричные уравнения и системы линейных уравнений
- •Решение систем линейных уравнений с помощью обратной матрицы
- •1.5. Собственные числа и собственные векторы матрицы
- •Глава 2. Векторная алгебра
- •§2.1 Векторы. Линейные операции над векторами
- •§2.2. Скалярное произведение
- •Свойства скалярного произведения
- •§2.3. Векторное произведение векторов
- •Свойства векторного произведения
- •§2.4. Смешанное произведение трех векторов
- •Глава III. Аналитическая геометрия
- •§ 3.1. Прямая линия на плоскости
- •Угол между двумя прямыми
- •Расстояние от точки до прямой
- •§ 3.2. Кривые второго порядка на плоскости
- •§ 3.3. Общее уравнение кривых второго порядка Преобразование уравнения кривой второго порядка к каноническому виду
- •§ 3.4. Плоскость в пространстве
- •§ 3.5. Прямая в пространстве. Прямая и плоскость
- •Глава IV. Математический анализ
- •§4.1. Основные элементарные функции, некоторые свойства и графики
- •§4.2. Предел функции. Замечательные пределы. Непрерывность функции
- •Замечательные пределы
- •Непрерывность функции
- •Разрывы функции
- •§4.3. Дифференцирование функций. Основные формулы дифференцирования
- •Основные правила дифференцирования
- •§4.4. Уравнения касательной и нормали к плоской кривой
- •§4.5. Производные высших порядков. Правила Лопиталя
- •Правила Лопиталя
- •§4.6. Монотонность функций. Экстремумы. Наибольшее и наименьшее значения функции на отрезке
- •§4.7. Промежутки выпуклости, вогнутости графика функции. Точки перегиба. Асимптоты
- •§4.8. Параметрически заданные функции. Векторная функция скалярного аргумента. Кривизна плоской кривой
- •Список рекомендуемой литературы
§4.5. Производные высших порядков. Правила Лопиталя
Пусть дана функция
y=f(x);
производная от этой функции
y′=f′(x).
Производная от этой производной
называется производной
второго порядка
функции y=f(x),
которая обозначается как y"
или f"(x)=![]() .
.
Аналогично
определяются производные более высокого
порядка f
(n)(x)=![]() .
.
Правила Лопиталя
Первое правило. Неопределенность .
Если
![]() ,
то
,
то
![]() .
.
Второе правило.
Неопределенность
![]() .
.
Если
![]() ,
то
.
,
то
.
Неопределенности вида 0∞; ∞-∞; 1∞;00 сводятся к неопределенностям , путем алгебраических преобразований.
______________
4.5.1. Найти производные второго порядка:
а)
y=cos2x;
б)
y=arctgx2 ;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() .
.
4.5.2. Найти f'(0), f"(0), f"'(0) если f(x)=e2xsin3x.
4.5.3. Вывести формулу для производной n – го порядка для функций:
а) y=xm; б) у=ах.
4.5.4. Найти пределы:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() ;
з)
;
;
з)
;
и)
![]() ;
к)
;
к)
![]() .
.
_________________
4.5.5. Найти производные второго порядка:
а) у=(х2-10х+5)5; б) y=sin2x;
в)
![]() ;
г) у=ln(x3-2x2+4).
;
г) у=ln(x3-2x2+4).
4.5.6. Найти выражение для n-й производной следующих функций:
а) у=3х; б) у=cosx; в) y=sin2x.
4.5.7. Найти пределы:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
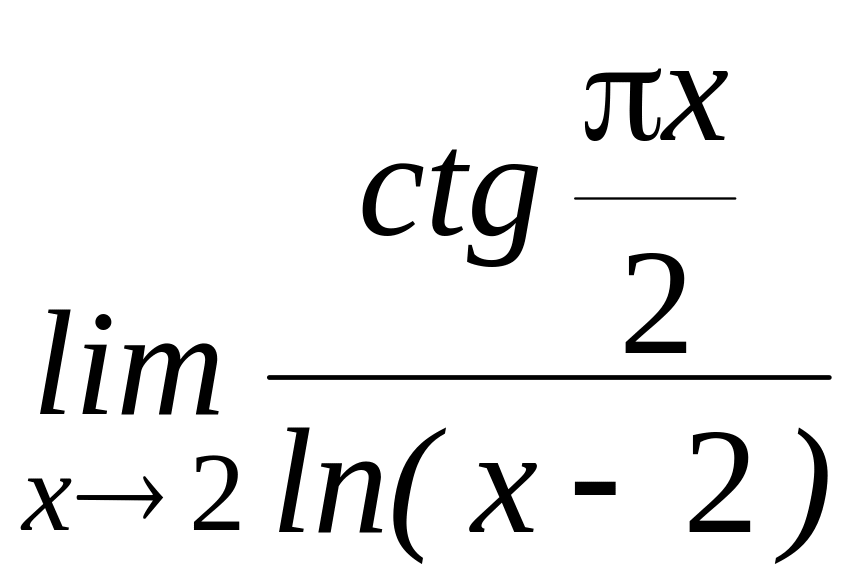 ;
;
ж)
![]() ;
з)
;
з)
![]() ;
;
и)
![]() ;
к)
;
к)
![]() .
.
§4.6. Монотонность функций. Экстремумы. Наибольшее и наименьшее значения функции на отрезке
Функция f(x) называется возрастающей в точке х0, если в некоторой - окрестности этой точки f(x0-h)<f(x0)<f(x0+h).
Убывающей – если f(x0+h)<f(x0)<f(x0-h), где 0<h<.
Функция f(x) называется возрастающей на отрезке [a,b], если для любых х1 и х2 этого отрезка из неравенства х1>х2 следует неравенство f(х1)>f(х2). Если же из неравенства х1>х2 следует, что f(х1)<f(х2), то функция f(x) – убывающая на отрезке [a,b].
Можно сформулировать достаточные признаки возрастания и убывания функции y=f(x)
Если y'>0 для всех х[a,b], то функция возрастает на [a,b]; при y'<0 для х[a,b], то функция на [a,b] убывает.
Функция f(x) может иметь экстремум лишь в тех точках, в которых f'(x)=0 или не существует. Такие точки называются критическими, или стационарными, или подозрительными на экстремум. Равенство нулю первой производной данной функции является необходимым условием существования экстремума.
В качестве достаточного условия существования экстремума в критической точке х0 можно принять смену знака первой производной при переходе через критическую точку, при этом, если знак меняется с + на -, то в точке х0 – максимум, если с – на + , то в точке х0 – минимум.
Если производная y' знак не меняет при переходе через точку, подозрительную на экстремум, то экстремума в этой точке нет.
Для отыскания наибольшего и наименьшего значений функций у=f(x) на отрезке [a,b] необходимо найти критические точки, принадлежащие [a,b]. Вычислить значения функции в этих критических точках и на концах отрезка. Из всех найденных значений выбираем наибольшее и наименьшее.
__________________
4.6.1. Найти интервалы монотонности следующих функций:
а) у=2-3х+х3; б) у=хе-х;
в) у=(х-2)2(х+2); г) y=ln(x2-2x+4).
4.6.2. Найти экстремумы функций:
а)
![]() ;
б) y=ln(x2+1);
;
б) y=ln(x2+1);
в)
![]() ;
г) у=(х-1)6/7.
;
г) у=(х-1)6/7.
4.6.3. Найти наибольшее и наименьшее значения функций на заданном отрезке:
а) у=х4+2х2+5,
х[-2,2];
б)
![]() ,
х[-6,8];
,
х[-6,8];
в) , х[0,4]; г) y=2tgx-tg2x, х[0,π/2].
_______________
4.6.4. Найти интервалы монотонности следующих функций:
а) у=(2-х)(х+1)2; б) у=х3-6х+5;
в) у=х+е-х; г) y=xlnx.
4.6.5. Найти экстремумы функций:
а)
![]() ;
б)
;
б)
![]() .
.
4.6.6. Найти наибольшее и наименьшее значения функций на отрезке:
а)
![]() ,
х[0,4];
б)
,
х[0,4];
б)
![]() ,
х[0,1];
,
х[0,1];
в)
![]() ,
х[0,1].
,
х[0,1].
