Приклади розв’язання завдань

Приклад 7.1. Вважаємо, що можлива відмова лише одного елемента.

Рисунок 7.1 – Функціональна модель об’єкта

Кожна можлива для даної моделі перевірка припускає контроль реакції одного з елементів на зовнішню взаємодію, що прикладена до об’єкта. Кожному і-му елементу поставлена у відповідність _і перевірка.

За заданою функціональною схемою будується її граф G=G(s) (рис. 7.2), де функція G(s) – множина якимось чином з’єднаних точок s, що називаються вершинами. Лінія, що з’єднує дві вершини, називається ребром графа Р_ij (s_i, s_j – кінці ребра Р_ij). Якщо Р_ij=Р_ji, то ребро є неорієнтованим ребром, у іншому випадку – орієнтованим. Орієнтоване ребро називають дугою графа. У загальному випадку ребро Р_ii також є ребром графа і називається петлею вершини графа.

Вершини 1 – 6 – відповідають елементам функціональної схеми; Р_ij – відповідні дуги графа; Р₁₂, Р₂₃ й т.д. – прямі гілки графа; Р₅₄ – зворотна гілка;

Р₁₁ – Р₆₆ – для того, щоб підкреслити залежність реакції елемента від його внутрішнього стану, виражену в тому, що при відмові і-го елементу на його виході спостерігається неприпустима реакція навіть при припустимому вхідному впливові, доповнюємо всі вершини петлями.

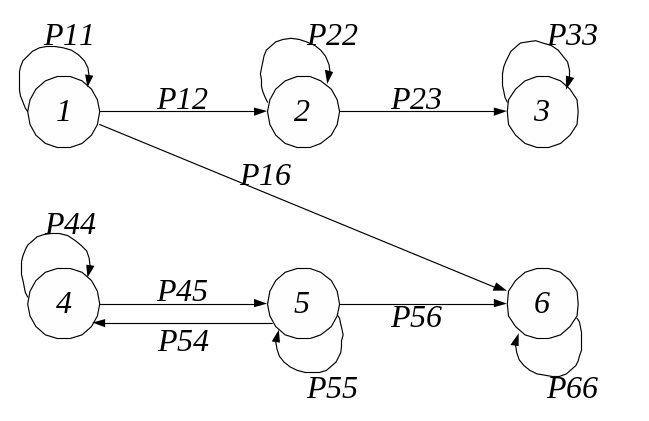
Рисунок 7.2 – Вихідний граф функціональної моделі об´єкта

Складаємо таблицю несправностей, у котрій “0” відповідає випадку, коли відбулася відмова елемента та “1” – якщо елемент працездатний.

Таблиця 7.1 – Таблиця несправності

S	π1	π2	π3	π4	π5	π6
S1
S2
S3
S4
S5
S6

С кладаємо матрицю суміжності, в котрій ставимо “1”, якщо в графі існує дуга, що з’єднує і–ту вершину з j–тою, та “0” – якщо дуги немає.

	1	1	1	0	0	0	1
	2	0	1	1	0	0	0
B=	3	0	0	1	0	0	0
	4	0	0	0	1	1	0
	5	0	0	0	1	1	1
	6	0	0	0	0	0	1

5 . Складаємо матрицю, в якій ставимо “1”, якщо існує шлях від і–тої вершини до j–тої вершини, та “0” – якщо його немає.

	1	1	1	1	0	0	1
	2	0	1	1	0	0	0
D=	3	0	0	1	0	0	0
	4	0	0	0	1	1	1
	5	0	0	0	1	1	1
	6	0	0	0	0	0	1

Нерозрізнені відмови – відмови елементів, які мають однакові строки в матриці D; їх можна визначити також за матрицею В, для цього закреслимо строки, що складаються лише з однієї одиниці та стовпці, номери яких співпадають з номерами закреслених строк. Повторюючи такі дії, можна отримати два результати: 1) усе буде закреслено (не існує нерозрізнених відмов); 2) строки та стовпці, що залишаться, будуть складатися з не менше двох одиниць. Саме вони вкажуть елементи, відмови яких нерозрізнені.

У нашому випадку нерозрізненим відмовам відповідають перевірки вершин 4 та 5, тому необхідно перетворити вихідний граф до виду, котрий виключить появу нерозрізнених відмов.

Побудова діагностичних тестів.

Перевірковий тест (тест для перевірки працездатності) складається з набору перевірок, виконання яких необхідне для виявлення факторів відмови кожної вершини графа.

Локалізуючий тест – набір перевірок, виконання яких необхідне для визначення місцезнаходження вершини, що відмовила.

Повний або діагностичний тест дорівнює сумі перших двох тестів.

Для побудови тестів необхідно перетворити вихідний граф наступним чином: нехай граф G(s) складається з однієї або декількох множин вершин, відмови яких нерозрізнені. До кожної такої множини застосуємо операцію “стягування”, котра зводиться до того, що всі дуги, які з’єднують вершини опускаються, а самі вершини об’єднуються в нову вершину. Тоді матриця шляхів матиме вигляд:

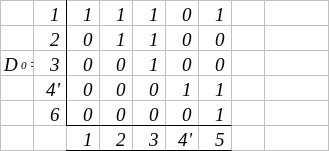
За отриманою матрицею будуємо новий граф станів G₀ (рис. 7.3):

Рисунок 7.3 – Новий граф функціональної моделі об’єкта

Розподілимо вершини за рангами.

Строки та стовпці матриці D₀ можна переставити таким чином, щоб усі числа d_ij, які стоять нижче головної діагоналі, дорівнювали нулю. З D₀ викреслюємо всі строки та стовпці, що відповідають вершинам виходу (3 та 6) і знаходимо вершини входу, які є вершинами першого рангу – вершини 1 та ; закреслимо стовпці та строки, що належать їй. В отриманій матриці вершини 1 та – вершини першого рангу; вершина 2 – вершина другого рангу; вершини 3 та 6 – вершини третього рангу.

	1	1	1	1	0	1
	4’	0	0	0	1	1
D0'=	2	0	1	1	0	0
	3	0	0	1	0	0
	6	0	0	0	0	1

Розглянемо отриманий граф G₀.

Нехай строки графу підпорядковані відповідно до рангів вершин таким чином, що номер вершини графа G₀ визначають номер перевірки, то для побудови діагностичних тестів достатньо перерахувати номери вершин G₀, що входять у відповідний тест.

Кількість перевірок, що входять до тесту, є довжиною тесту. Будь-який тест, що належить до сукупності локалізуючого, перевіркового або повного тестів та має мінімальну довжину відносно до інших тестів з тієї самої сукупності, має назву мінімального.

Для того, щоб перевірковий тест вихідного графа був мінімальним, необхідно і достатньо, щоб до нього ввійшли всі вершини типу “вихід”, тобто T_Пmin = {π₃, π₆}.

Для побудови мінімального локалізуючого тесту в матриці знаходять такий мінімальний набір вершин, що після викреслювання з матриці стовпців відповідних вершин, які не входять до даного набору, всі строки отриманої матриці залишаються попарно розрізненими, при цьому, якщо якась з вершин G₀ має лише одну вихідну з неї дугу, то ця вершина обов’язково входить до локалізуючого тесту. Тобто

Т_Л1={π₂, π₆}; Т_Л2={π₃}; Т_Л3={π₅};Т_Л4={π₆}.

Повний тест може бути отриманий з мінімальних перевірковий та локалізуючого тестів, при цьому довжина його відповідає сумі довжин Т_Пmin та Т_Лmin. Після викреслювання в цій сумі кожної з двох і більше дублюючих перевірок, отримуємо мінімальний повний тест:

Т_min= T_Пmin + T_Л1min = {π₂, π₃, π₆}.