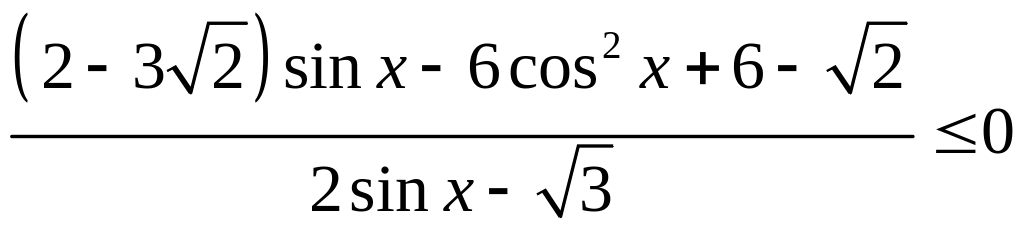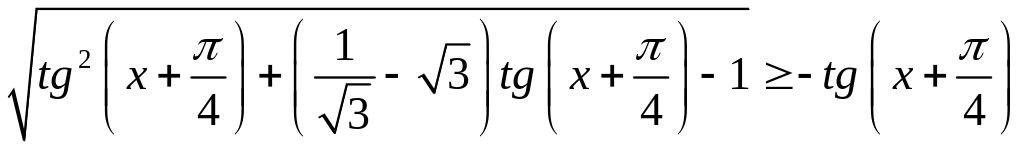- •Робоча програма з курсу елементарної математики
- •Програма
- •Тема 4. Задачі на складання рівнянь та нерівностей. Задачі на відсотки та числові залежності. Задачі на рух і роботу. Задачі на суміші.
- •Тема 7. Доведення нерівностей. Властивості числових нерівностей. Основні методи доведення нерівностей.
- •Тематика та зміст практичних занять. Практичне заняття № 1-2
- •Практичне заняття № 3-4
- •Заняття №3
- •Заняття №4
- •Практичне заняття № 5-6 Тема: Рівняння та нерівності, що містять змінну під знаком модуля
- •Заняття №5
- •Заняття №6
- •Практичне заняття № 7
- •Контрольна робота № 2
- •Практичне заняття № 8-9
- •Тема: Доведення нерівностей..
- •Практичне заняття № 10-11 Тема: Методи розв’язування систем рівнянь.
- •Практичне заняття № 12-13 Тема: Задачі на складання рівнянь та нерівностей.
- •Практичне заняття № 14-17 Тема: Тригонометричні функції числового аргументу. Тотожні перетворення тригонометричних функцій. Тригонометричні рівняння та нерівності.
- •Практичне заняття № 18 Контрольна робота № 2
- •Питання до екзамену
- •Індивідуальне завдання №1 «Ірраціональні рівняння та нерівності»
- •Розв’язати ірраціональні рівняння. Письмово проаналізувати причини виникнення стороніх коренів:
- •Розв’язати ірраціональну нерівність:
- •Індивідуальне завдання №2 «Показникові та логарифмічні рівняння та нерівності»
- •2. Використовуючи метод логарифмування розв'язати рівняння (додаткове):
- •Індивідуальне завдання №3 «Рівняння та нерівності, що містять змінну під знаком модуля ь»
- •Індивідуальне завдання №4 «Методи розв’язування лінійних та нелінійних систем рівнянь»
- •Індивідуальне завдання №5 «Задачі на складання рівнянь та нерівностей»
- •Індивідуальне завдання №6 «Доведення нерівностей»
- •1. Довести нерівність:
- •2. Довести умовну нерівність
- •Індивідуальне завдання №7«Тригонометричні рівняння та нерівності»
- •1. Розв’язати дане рівняння трьома способами: за допомогою формул подвійного кута, методом допоміжного кута та універсальної тригонометричної підстановки
- •3. Розв’язати нерівність :
- •4. Розв’язати тригонометричні рівняння (додаткове завдання)
Індивідуальне завдання №6 «Доведення нерівностей»
1. Довести нерівність:
2. Довести умовну нерівність
Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо , то
Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо
 ,
то
,
то

Довести, що якщо , то
Довести, що якщо , то
Довести, що якщо , то
Довести, що якщо , то
Довести, що якщо , то
Довести, що якщо , то
Довести, що якщо , то
Довести, що якщо , то
Індивідуальне завдання №7«Тригонометричні рівняння та нерівності»
1. Розв’язати дане рівняння трьома способами: за допомогою формул подвійного кута, методом допоміжного кута та універсальної тригонометричної підстановки
Довести, що отримані відповіді співпадають. (додаткове завдання)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
|
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
|
Розв’язати нерівність:
|
|
|
3. Розв’язати нерівність :
4. Розв’язати тригонометричні рівняння (додаткове завдання)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
|
14.
15.
16.
17.
18.
19.
20.
21.
22. 23.
23. 24.
25. |