Контрольный вопрос

5.3. Почему интерполяционное выражение для расчета диэлектрической проницаемости полупроводниковых твердых растворов имеет вид ?

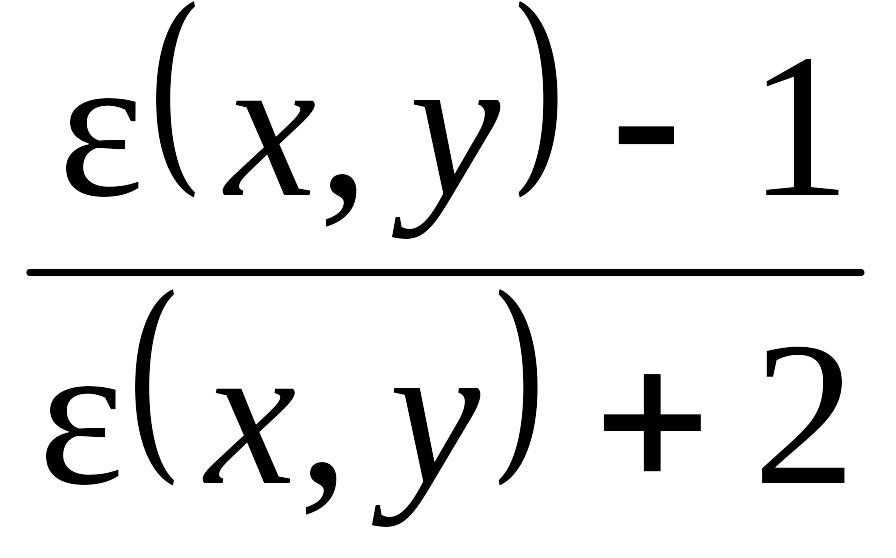Ответ. Интерполяционное выражение для диэлектрической проницаемости получено в приближении линейного характера интерполяции поляризуемости отдельных атомов (молекул) α₀. Диэлектрическая проницаемость ε и поляризуемость α₀ связаны соотношением Клазиуса−Мосотти:

~ α₀.

Примечание. Расчет свойств многокомпонентных материалов, безусловно, должен быть привязан к приборным реализациям. Напомним основные разновидности лазерных гетероструктур: односторонние гетероструктуры, двойные гетероструктуры, лазеры с раздельным ограничением, варизонные гетероструктуры [18].

В односторонних гетероструктурах активный слой расположен между p−n-переходом и изотипным гетеропереходом, отделяющим его от более широкозонного полупроводника. Если активная область имеет проводимость р-типа, то условная запись такой структуры имеет вид: п – р* – Р, где прописная буква использована для обозначения широкозонного материала, а звездочкой обозначена активная область. Пассивные области гетероструктуры называют п- и р-эмиттерами, поставляющими в активную область электроны и дырки соответственно.

В двойных гетероструктурах оба эмиттера представляют собой материал более широкозонный по отношению к активной области. Такие структуры могут быть типа Р – р*– N и Р – п*– N. Двойные гетероструктуры обеспечивают не только электронное, но и оптическое ограничение. Значение коэффициента преломления ń у широкозонных твердых растворов, как правило, меньше, чем у узкозонной активной области.

Гетероструктуры с раздельным ограничением содержат между широкозонными Р- и N-областями не один, а несколько слоев с меньшими значениями ширины запрещенной зоны.

Простейшей из гетероструктур с раздельным ограничением является гетероструктура типа Р – Р^l – n*– N^l – N или N – N^l – р*– Р^l– Р, где эмиттерные слои Р^l и N^l имеют промежуточные значения ширины запрещенной зоны между активным слоем и слоями Р и N. В такой структуре появляется возможность раздельно управлять толщиной активного слоя, в котором наблюдается электронное ограничение, и толщиной волноводного слоя, обеспечивающего оптическое ограничение. Толщина волноводного слоя, соответственно, равна сумме толщин активного слоя и эмиттерных слоев Р^l и N^l.

В варизонных структурах гетерограницы размыты в некоторые переходные области с переменным значением ширины запрещенной зоны. В таких областях возникает так называемое квазиэлектрическое поле, связанное с градиентом ширины запрещенной зоны, что используется для повышения эффективности сбора носителей заряда в активной области.

Детальное рассмотрение особенностей волноводных свойств в перечисленных гетероструктурах относится к физике приборов и выходит за рамки материаловедческих задач, рассматриваемых в данном издании.

5.5. Расчет упругих напряжений и деформаций

Процессы эпитаксиального роста протекают по механизму псевдоморфизма в случае незначительного различия периодов решетки подложки и эпитаксиального слоя. Когерентность гетерограницы в этом случае обеспечивается процессом смещения атомов из своих положений равновесия, который компенсирует несоответствие межатомных расстояний. При когерентном сопряжении фаз не нарушается макроскопическая сплошность материала и кристаллографические плоскости непрерывно переходят из подложки в эпитаксиальный слой. Однако при этом изменяются межплоскостные расстояния в направлении, параллельном и перпендикулярном гетерогранице. В случае кубической симметрии сопрягаемых материалов когерентное срастание решеток по плоскости (100) сопровождается тетрагональным искажением кристаллической решетки, а при эпитаксии на плоскость (111) искажения носят ромбоэдрический характер. В плоскости гетерограницы появляются внешние упругие напряжения, называемые напряжениями несоответствия, и связанные с ними деформации.

В общем случае соотношения между компонентами тензора напряжений σ_ij и деформаций ε_kl устанавливает закон Гука [21]: σ_ij = c_ijkl ε_kl, где c_ijkl – компоненты упругих постоянных тензора 4-го ранга.

Тензор 4-го ранга в общем случае содержит 81 компоненту (3⁴). В силу симметричности тензоров ε_ij и Т_ij (ε_ij = ε_ji и σ_ij = σ_ji) число независимых компонент c_ijkl сокращается до 36. Из термодинамических соображений следует, что если деформирующие силы консервативны, то коэффициенты c_ijkl симметричны также и относительно перестановки пар индексов: c_ijkl и c_klij (при i, j, k, l = 1, 2, 3).

Задача 5.25. Используя симметричность индексов у упругих постоянных c_ijkl, представить уравнение σ_{ij =} c_ijkl ε_kl в матричном виде σ_m = c_mnε_n. Показать связь между σ_m и σ_ij; ε_n и ε_kl; c_mn и c_ijkl.

Решение. В соответствии с так называемым правилом "девятки" (сумма двух неодинаковых индексов и третьего, их замещающего, должна быть равна 9, т. е. (2 + 3) + 4 = 9; (3 + 1) + 5 = 9; (1 + 2) + 6 = 9, получим: σ₁₁ → σ₁; σ₂₂ → σ₂; σ₃₃ → σ₃; σ₂₃ = σ₃₂ → σ₄; σ₁₃ = σ₃₁→ σ₅; σ₁₂ = σ₂₁ → σ₆. Аналогично производится перенумерация компонент деформации ε_kl. В этом случае матрица упругих постоянных c_mn может быть представлена через c_mn в виде:

εn σn
	с1111	с1122	с1133	с1123	с1113	с1112
				с 1132	с1131	с1121
	с2211	с2222	с2233	с2223	с2213	с2212
				с 2232	с2231	с2221
	с 3311	с3322	с3333	с 3323	с3313	с3312
				с 3332	с3331	с3321
	с2311	с2322	с2333	с 2323	с2313	с2312
				с 2332	с2331	с2321
	с3211	с3222	с3233	с 3223	с3213	с3212
				с 3232	с3231	с3221
σ5	с 1311	с1322	с1333	с 1323	с1313	с1312
				с 1332	с1331	с1321
	с3111	с3122	с3133	с 3123	с3113	с3112
				с 3132	с3131	с3121
σ6	с1211	с1222	с1233	с 1223	с1213	с1212
				с 1232	с1231	с1221
	с2111	с2122	с2133	с 2123	с2113	с2112
				с2132	с2131	с2121

Таким образом, для тензоров 4-го ранга можно сформулировать дополнительные правила:

c_mn = c_ijkl, если m и n равны 1, 2, 3;

c_mn = 2c_ijkl, если m или n равно 4, 5, 6.

Например, с₁₄ = c₁₁₂₃ + c₁₁₃₂ = 2c₁₁₂₃;

c_mn = 4 c_ijkl, если m и n равны 4, 5, 6.

Например, с₄₅ = c₂₃₁₃ + c₂₃₃₁ + c₃₂₁₃ + c₃₂₃₁ = 4c₂₃₁₃.

Необходимо подчеркнуть, что упругие постоянные c_mn не являются тензором. Эти компоненты не преобразуются как компоненты тензора, при их преобразовании необходимо возвращаться к четырехиндексным обозначениям.

В тензоре упругости только для класса кристаллов, отвечающего триклинной сингонии, существует 21 независимая компонента для упругих постоянных. Для всех остальных классов часть коэффициентов обращается в нуль вследствие свойств симметрии кристалла. В кубической сингонии всего 9 компонент упругих постоянных отличны от нуля, из них только 3 являются независимыми: с₁₁ = c₂₂ = c₃₃; с₁₂ = c₁₃ = c₂₃; с₄₄ = c₅₅ = c₆₆.

Справочные данные об упругих постоянных приведены в табл. П 1, П 3, П 4 Приложения.

Для расчета коэффициентов упругости в многокомпонентных твердых растворах используют методы линейной интерполяции. Для твердых растворов A_xB_yC_1–x–yD такая интерполяция для коэффициента упругости имеет вид c_mn(х, у) = хc_mn(AD) + yc_mn(BD) + (1 – x – y) c_mn(CD); для твердых растворов A_хB_1–хC_уD_1–y линейная интерполяция может быть записана так: c_mn(х, у) =

= ху c_mn(AС) + х(1 – y)c_mn(АD) + (1 – x)уc_mn(ВС) + (1 – x)(1 – y)c_mn(ВD).

В общем случае c_mn зависит от температуры, но, как правило, в интервале от 300 до 1000 К изменения значений c_mn не превышают 10 %, поэтому в оценочных расчетах их не учитывают.

Если толщина подложки H много больше толщины эпитаксиального слоя h (Н >> h), то деформация в слое становится однородной и изгибом структуры и деформацией подложки можно пренебречь. В плоскости гетерограницы нормальные напряжения и деформации одинаковы (ε₁ = ε₂ и σ₁ = σ₂), а касательные напряжения отсутствуют (σ₄ = σ₅ = σ₆ = 0). По направлению нормали к плоскости роста напряжение σ₃ = 0, т. е. эпитаксиальный слой не нагружен, однако деформация ε₃ отлична от нуля.

Значения напряжений и деформаций, возникающих на гетерогранице при когерентном сопряжении двух решеток, зависят от их кристаллографической ориентации.

Если эпитаксия проводится на плоскость (100), то химически обусловленное несоответствие периодов решетки f₀, определяющее деформации в плоскости гетерограницы ε₁ и ε₂, можно рассчитать по следующему выражению:

f₀ = = – ε₁,

где a₀ – параметр кристаллической решетки эпитаксиального слоя твердого раствора, a_s – параметр кристаллической решетки подложки.

Задача 5.26. Определить упругие напряжения σ₁ и σ₂ в плоскости гетерограницы "подложка – эпитаксиальный слой", если параметр решетки подложки a_s, а равновесное значение параметра решетки эпитаксиального слоя a₀. Найти значения деформаций ε₁, ε₂, ε₃, а также рассогласование параметров решетки в направлении, перпендикулярном гетерогранице . Считать, что подложка и эпитаксиальный слой относятся к кубической сингонии, рост осуществляется по плоскости (100).

Решение. Из условия задачи следует, что σ₁ = σ₂ и σ₃ = 0. Аналогично σ₄ = σ₅ = σ₆ = 0 и ε₄ = ε₅ = ε₆ = 0.

Найдем значения деформаций ε₁ и ε₂. По определению химически обусловленное рассогласование периодов решетки f₀ определяется следующим образом: f₀ = = – ε₁ = – ε₂. Запишем выражение для расчета напряжения в направлении, перпендикулярном гетерогранице:

σ₃ = c₃₁ε₁ + c₃₂ε₂ + c₃₃ε₃ + c₃₄ε₄ + c₃₅ε₅ + c₃₆ε₆ = c₁₂ε₁ + c₁₂ε₁ + c₁₁ε₃ = 0. Отсюда

ε₃ = = . Тогда напряжения в плоскости гетерограницы

σ₁ = σ₂ = c₁₁ε₁ + c₁₂ε₂ + c₁₃ε₃ = c₁₁ε₁ + c₁₂ε₂ = =

= .

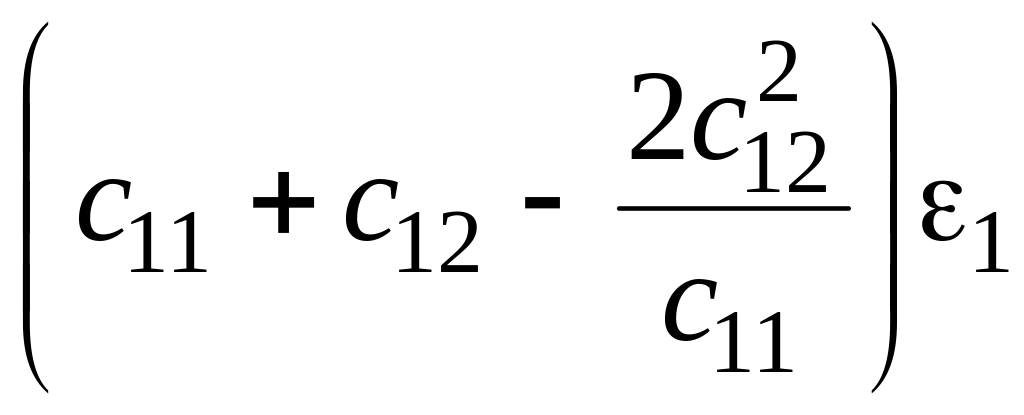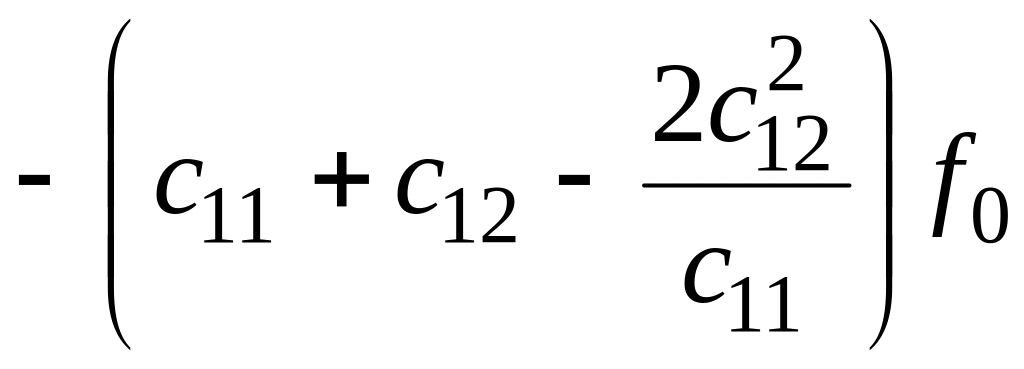Рассогласование параметра решетки в направлении, перпендикулярном гетерогранице :

.

Примечание. Обратить внимание на значения c_mn в табл. П 1: c₁₂ ≈ c₄₄;

c₁₁ ≈ 2 c₁₂, т. е. ≈ 2 f₀.

Задача 5.27. Рассчитать плотность упругой энергии (упругая энергия единицы объема) деформированного слоя твердого раствора по условию задачи 5.26.

Решение. По определению

= =

.

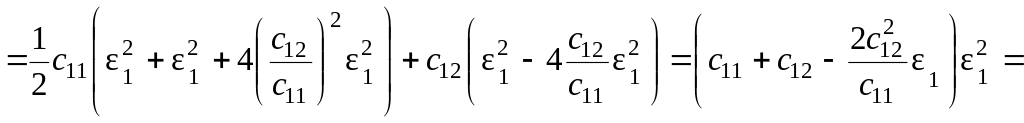
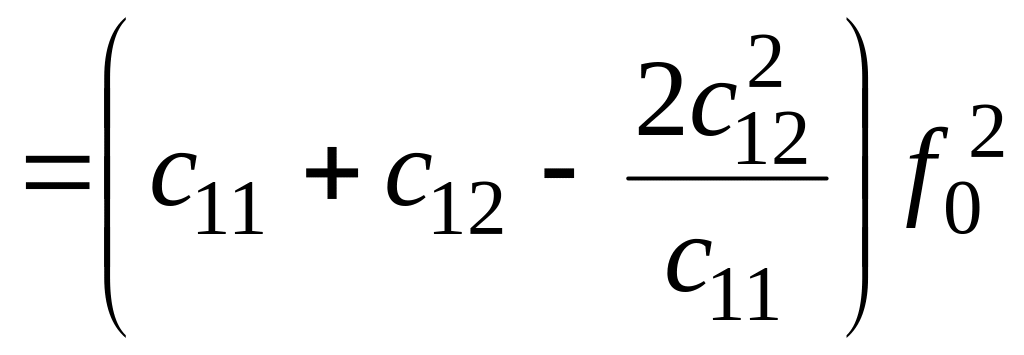Задача 5.28. Рассчитать упругодеформированное состояние гетероструктуры, если подложка и эпитаксиальный слой относятся к кубической сингонии, рост осуществляется по плоскости (111).

Решение. При ориентации подложки и слоя в плоскости (111) расчетные соотношения принимают следующий вид:

f₀ = = –ε₁; ε₁= ε₂ ≠ ε₃

; ;

;

; σ₃ = 0;

= .

Задача 5.29. Закон Гука в тензорном виде может быть записан следующим образом:

σ_ij = c_ijkl ε_kl или ε_ij = s_ijkl σ_kl,

где c_ijkl – коэффициенты упругой жесткости (модули упругости), s_ijkl – коэффициенты упругой податливости.

Для кристаллов кубической сингонии найти выражения для коэффициентов s₁₁, s₁₂, s₄₄ для GaAs.

Ответ: ; ;

.

Примечание. Эти соотношения можно записать в более компактной форме:

; ; .

Задача 5.30. Объяснить физический смысл коэффициентов упругой жесткости с₁₁, с₁₂ и с₄₄ для кристаллов кубической сингонии.

Решение. Физическая сущность коэффициента с₄₄ очевидна. Этот коэффициент является мерой сопротивления деформации, вызывающей скалывающие напряжения, приложенные в плоскости (100) в направлении [010].

Коэффициенты с₁₁, с₁₂ не имеют прямой физической интерпретации, однако их линейные комбинации имеют простое объяснение:

, ,

где К – объемная упругость или сопротивление сжатию (мера сопротивления деформации, вызываемой гидростатическим давлением); G – мера сопротивления деформации в плоскости (100) в направлении [110].

Задача 5.31. В научно-технической справочной литературе основными физическими величинами, характеризующими упругие механические свойства конструкционных материалов, являются модуль нормальной упругости Е и коэффициент Пуассона ν.

Модуль упругости (модуль Юнга) Е – коэффициент пропорциональности между нормальным напряжением и относительным удлинением.

Коэффициент Пуассона ν – абсолютное значение отношения поперечной деформации к продольной.

Рассмотреть случай однородной деформации изотропного (поликристаллического) стержня вдоль оси z при простом растяжении (сжатии). Определить выражения для Е и ν через коэффициенты упругой жесткости с_mn (через коэффициенты К и G) для кристаллов кубической сингонии.

Решение. По условию испытания упругих свойств материала силы действуют равномерно на всю поверхность торцов стержня. Сила, действующая на единицу площади поверхности: σ _≡ σ₃₃ = σ₃. По определению ε_ij = s_ijkl σ_kl, и тогда, в соответствии с решением задачи 5.30 получим:

;

Отметим, что с₁₁ – с₁₂ = 2G; с₁₁ + 2с₁ = 3К. Тогда

; ;

.

По определению модуль Юнга (или модуль нормальной упругости Е) − величина, обратная коэффициенту, связывающему σ₃₃ и ε₃₃:

.

Коэффициент Пуассона (отношение поперечного сжатия ε₁₁ к продольному растяжению ε₃₃)

.

Задача 5.32. Схема эксперимента по условию задачи 5.31 позволяет легко определить модуль Юнга Е и коэффициент Пуассона ν, а затем найти значения G и К и вычислить с₁₁ и с₁₂. На практике металловеды широко используют оценочные соотношения ; .

Используя решение задачи 5.31 вывести уравнения, определяющие значения G и К через модуль Юнга Е и коэффициент Пуассона ν. Показать, что выражения, применяемые в металловедении при оценке G и К через модуль Юнга Е, теоретически обоснованы для значения коэффициента Пуассона ν = 0,33. (Значения коэффициента Пуассона ν близки к 0,33 для большинства металлических материалов, но не для всех.)

Ответ: ; .

Задача 5.33. В задаче 5.26 проведен анализ упругодеформированного состояния эпитаксиального слоя в приближении отсутствия пластической деформации. В реальных системах может происходить частичная пластическая деформация. Спланировать эксперимент по оценке напряженного состояния в гетероструктуре.

Ответ. Экспериментально определяется рассогласование параметров решетки подложки и слоя в направлении, перпендикулярном гетерогранице . С использованием выражений, полученных при решении задачи 5.26, оцениваются значения f₀, σ₁, ε₃, ε₁.

Примечание. По сравнению остаточной упругой деформации с полной упругой деформацией может быть оценена величина пластической деформации.

Задача 5.34. Что можно сказать о физическом состоянии кристалла, если матрица тензора напряжений σ_ij имеет следующий вид:

– р	0	0
0	– р	0
0	0	– р

Как изменится ширина запрещенной зоны полупроводников А³В⁵ и твердых растворов на их основе? Как изменится ширина запрещенной зоны полупроводников А⁴В⁶ (халькогенидов свинца, халькогенидов олова)? Получить количественные оценки для конкретных материалов, заданных преподавателем.

Указания. Случай, когда σ_ij = – рδ_ij, соответствует всестороннему сжатию или растяжению (гидростатическое давление). Поэтому при расчетах ширины запрещенной зоны следует воспользоваться значениями коэффициентов , приведенными в табл. П 3 Приложения. Обратить внимание на аномальные значения для халькогенидов свинца.

Задача 5.35. В полупроводниках А³В⁵ потолок валентной зоны находится в (∙) Г зоны Бриллюена (см. рис. 5.1). В (∙) Г происходит вырождение. Как изменится энергетическая зонная структура при упругой деформации? Предложить план эксперимента по анализу упругодеформированного состояния с использованием возникающего эффекта.

Ответ. В (∙) Г снимается вырождение. В зависимости от характера деформации зона легких дырок находится выше (при сжатии) или ниже (при растяжении) зоны тяжелых дырок. При люминесценции наблюдается переходы из зоны проводимости в две подзоны: легких и тяжелых дырок. Излучение в подзону легких дырок поляризовано параллельно оси деформации, а в подзону тяжелых дырок – перпендикулярно оси деформации. Таким образом, можно раздельно оценивать энергетические зазоры между зоной проводимости и валентными зонами легких и тяжелых дырок и диагностировать характер деформации.